【小白学机器学习5】评价预测值和观测值差异的指标：MSE, RMSE,MAE, MAPE, WMAPE

奔跑的犀牛先生

已于 2024-03-10 12:32:41 修改

阅读量7.3k

点赞数 28

分类专栏：机器学习文章标签：概率论

于 2024-02-29 13:52:14 首次发布

本文链接：https://blog.csdn.net/xuemanqianshan/article/details/136362781

版权

机器学习专栏收录该内容

45 篇文章

订阅专栏

本文详细探讨了评价误差的各种度量指标，如最小二乘法、MSE、RMSE、MAE和MAPE，解释了它们的起源、计算方法和特点，以及在回归模型评估中的应用。文章还介绍了范式概念和L1/L2范式的区别。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

2.1 误差问题的由来：回归模型预测值和真实值的差距

2.2 误差Y=f(X)+ ε 其中的， ε 是模型不能解释的误差，模型外的不可控因素

2.3 如何评价某模型 /某函数的预测值是否足够好？

2.3.1 只存在3种类型的值

2.3.2 为了比较Y^=f(x)+ε 中 ε的好坏，就推出了最小二乘法

2.4 最小“二乘”法：其实应该叫最小“乘方”法

3.1 插播知识: 什么是范式和L1,L2范式

3.2 各种指标

3.3 MSE 均方差损失（ Mean Squared Error Loss）

1 评价误差的各种度量指标

1.1 评价什么误差？

一般我们用一个模型的预测曲线，去拟合和预测我们之前的观测数据
但是，预测数据和观测数据肯定是有误差的
那我们要如何，评价误差的多少，进而评价模型的好坏呢？
前人发明了各种指标，如下

1.2 评价误差有各种指标

评价误差有各种指标，那么什么时候应该用什么指标合适？要搞清楚这个，必须先了解每个指标的具体公式，意义，使用的差别。

这些评价指标里最经典方法就是，最小二乘法。从最小二乘这个评价标准开端，又衍生了各种各有优劣的评价方法和指标。

最小二乘法：Σ(Y-f(xi))**2
MSE
RMSE
MAE
MAPE
WMAPE
R**2
等等

2 从误差的评价开始捋这个问题

误差的由来，我们评价的是什么误差

2.1 误差问题的由来：回归模型预测值和真实值的差距

step1: 假设我们有自变量X，因变量Y。
- 这个自变量是x是，我们观测Y的依据，也是客观可记录的
- 而因变量Y是我们从自然界进行观测而记录下来的客观的值。
- 比如我们记录从1号到30号（日期是x）每天的温度(问题是Y)
step2: 我们经过计算和模拟得到模拟函数/预测函数 f(X)
step3: 然后我们用预测函数 f(X) 去模拟Y
- 因为试图根据折30天的温度数据，去预测第31天的温度
- 因此我们会模拟一个直线/曲线出来，但是这条线和前30天温度的散点图肯定是不完全匹配的，因此会产生误差。
step4: 但是预测函数和真实值之间一定是有误差的，Y=f(X)+ ε
step5: 那么如何评价不同的曲线Y=f(X)+ ε

2.2 误差Y=f(X)+ ε 其中的， ε 是模型不能解释的误差，模型外的不可控因素

误差Y=f(X)+ ε
其中的ε 是模型不能解释的误差，模型外的不可控因素

2.3 如何评价某模型 /某函数的预测值是否足够好？

2.3.1 只存在3种类型的值

真实值：只存在理想中，主观的
观测值：Y，客观存在的
预测值： Y^=f(x) ，对应每一个观测值，理论上只存在一个预测值。

2.3.2 为了比较Y^=f(x)+ε 中 ε的好坏，就推出了最小二乘法

但是，因为我们可能做多个模拟模型，有多个模拟函数/曲线，我们因此会有多个预测值，我们还需要比较不同模型的预测值Y^，哪个更好。
预测值：Y^=f(x) ，对应每一个真实值，对应的预测值根据预测函数可做出多个
然后现在怎么判断，预测值是否准确呢？
就到了最小二乘法了。

2.4 最小“二乘”法：其实应该叫最小“乘方”法

最小二乘法：应该叫最小乘方法，二乘就是指平方！

这个名字不直观，很容易误导我这样的新手。

2.4.1 基础特点

二乘就是指平方！
最小二乘法，衡量的是预测值和观察值之间的误差。
具体计算就是 Σi（ (观察值i-预测值i)**2）

2.4.2 最小二乘法

最小二乘法（又称最小平方法）是一种数学优化技术。
它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合，其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

2.4.3 公式

最小二乘法误差=Σ(Y-f(xi))**2

3 评价误差的各种标准

3.1 插播知识: 什么是范式和L1,L2范式

简单的理解，范式就是距离
L1 范式距离，就是 |y1-y2|
L2 范式距离，就是 (y1-y2)**2
以下类推
像我现在的水平，暂时了解到这么多即可。

3.2 各种指标

从最小二乘这个评价标准开端，又衍生了各种各有优劣的评价方法和指标

最小二乘法误差=Σ(Y-f(xi))**2
MSE
RMSE
MAE
MAPE
WMAPE

3.3 MSE 均方差损失（ Mean Squared Error Loss）

MSE 均方差损失（ Mean Squared Error Loss）
L2范式误差
L2 loss

3.3.1 计算公式

MSE，均方误差
MSE=Σ(Y-f(Xi))**2/i ，i=1~n
MSE=最小二乘误差/n

3.3.2 图形推导

推导

MSE=Σ(y^-y)^2/n
这个函数的抽象化
MSE=y=f(x)
MSE=y=f(x)=f(x^2)

这个图形是个二次曲线，有最小值
范围[0,+∞)，当预测值与真实值完全相同时为0，误差越大，该值越大
MSE 曲线的特点是光滑连续、可导，便于使用梯度下降算法，是比较常用的一种损失函数。
而且，MSE 随着误差的减小，梯度也在减小，这有利于函数的收敛

3.3.3 MSE的特点

不同商品真实值量纲上的差别带来的MSE结果波动大
极端值的影响，可以平衡
[0,1] 误差越小，平方值的MSE会越小
[1,∞] 误差越大，平方值的MSE会越大，惩罚性的把误差越大
不够直观（平方之后含义不好解释）

其中，y^为预测值，y为真实值。
对每期预测值和实际值的差值进行平方，然后再对多期差值的平方取平均值，得到平均均方误差。
平方的好处是放大极端误差：对误差进行平方，就是加倍“惩罚”那些极端误差，凸显那些极端虚高或虚低的预测值，也是我们应该重点避免的对象。
选择预测方法时，要尽量避免产生大错特错、极端误差的预测模型，用均方误差来量化预测准确度，能较好地排除这样的模型。

平方误差有个特性，就是当 yi 与 f(xi) 的差值大于 1 时，会增大其误差；
当 yi 与 f(xi) 的差值小于 1 时，会减小其误差。这是由平方的特性决定的。
也就是说， MSE 会对误差较大（>1）的情况给予更大的惩罚，对误差较小（<1）的情况给予更小的惩罚。
从训练的角度来看，模型会更加偏向于惩罚较大的点，赋予其更大的权重。
如果样本中存在离群点，MSE 会给离群点赋予更高的权重，但是却是以牺牲其他正常数据点的预测效果为代价，这最终会降低模型的整体性能。

3.4 RMSE

RMSE，开方均方误差 RMSE=sqrt(MSE)

Root Mean Square Error

3.5 MAE

3.5.1 L1 loss

MAE
L1 loss

3.5.2 计算公式

MAE=Σ|Y-f(Xi)|/n ，i=1~n

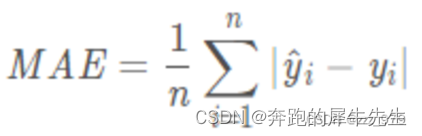
3.5.3 图形推导

3.5.4 MAE的特点

不同商品真实值量纲上的差别带来的MAE结果波动大

举例子

比如同样是 |yi^-yi|=5
有可能是6-1=5，但是百分比percent=(6-1)/1=5=500%，误差很大
也可能是105-100=5，但是百分比percent=(105-100)/100=5/100=5%，误差较小
也可能是1005-1000=5，但是百分比percent=(1005-1000)//1000=5/1000=0.5%，误差极小
可见，ABS都是5，但是百分比差别巨大！！

MAE 的曲线呈 V 字型，连续但在 y-f(x)=0 处不可导，计算机求解导数比较困难。
而且 MAE 大部分情况下梯度都是相等的，这意味着即使对于小的损失值，其梯度也是大的。
这不利于函数的收敛和模型的学习。
值得一提的是，MAE 相比 MSE 有个优点就是 MAE 对离群点不那么敏感，更有包容性。
因为 MAE 计算的是误差 y-f(x) 的绝对值，无论是 y-f(x)>1 还是 y-f(x)<1，没有平方项的作用，惩罚力度都是一样的，所占权重一样。

3.6 MAPE

Mean Absolute Percentage Error

当真实值 $y_{i}$ 非常小，特别是接近0时，MAPE可能很大
这个值很直观，但也容易误导：当实际值非常小，特别是接近0时，这一百分比可能很大；
如果实际值是0的话，分母就是0，计算没有意义。解决方案是设定上限，比如平均绝对百分比误差不超过100%。
MAPE 指平均绝对百分比误差，是一种相对度量，实际上将 MAD 尺度确定为百分比单位而不是变量的单位。平均绝对百分比误差是相对误差度量值，它使用绝对值来避免正误差和负误差相互抵消
MAPE 对相对误差敏感，不会因目标变量的全局缩放而改变，适合目标变量量纲差距较大的问题