高效的基于决策的黑盒攻击方法HSJA:HopSkipJumpAttack: A Query-Efficient Decision-Based Attack

高效的基于决策的黑盒攻击方法HSJA:HopSkipJumpAttack: A Query-Efficient Decision-Based Attack

一.介绍

本文研究了在优化框架下的基于决策的攻击，并提出了一系列新颖的算法，用于生成针对性和非针对性的对抗性示例，这些示例针对“ 2-距离”或“∞距离”的最小距离进行了优化。 该算法本质上是迭代的，每个迭代涉及三个步骤：梯度方向的估计，通过几何级数进行的步长搜索和通过二分法的边界搜索。对优化框架和梯度方向估计进行了理论分析。这不仅为选择超参数提供了参考，而且还激发了所提出算法中的必要步骤。将该算法称为HopSkipJumpAttack2。

贡献：

1. 仅基于对模型决策的访问，就提出了一种新颖的，无偏见的，在决策边界处的梯度方向估计，并提出了控制偏离边界的误差的方法。
2. 基于提出的估计和分析，设计了一系列算法HopSkipJumpAttack，该算法没有超参数，查询效率高，并且具有收敛性分析。
3. 通过广泛的实验，证明了所提出的算法优于几种基于决策的最新攻击方法的效率。
4. 通过对几种防御机制的评估，防御蒸馏，基于区域的分类，对抗训练和输入二值化等，论文认为提出的攻击可以用作研究人员评估新防御机制的简单有效的第一步。

二.方法

2.1 优化框架

分类器C（模型）：

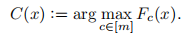
给定一些输入x*,定义如下这样一个函数Sx*:

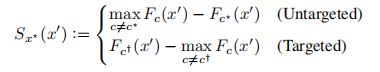
对于一个扰动图像x’,当且仅当Sx*(x’)>0,这是一个成功的攻击。在成功和不成功的扰动图片之间的边界的定义为：

论文使用布尔函数 φx来表示成功的扰动：

在基于决策的设置中，这个函数是可获得的，通过单独查询分类器C来计算函数值。一次对抗攻击的目标是产生对抗样本x’使得φx(x‘) = 1的同时，保证x’与原样本尽可能相似。可以被公式化为下面这个优化公式：

其中d是一个距离函数来衡量x’与x*的相似度，通常选择lp-norm（p=0,2, ∞）

2.2 对于l2距离的一个迭代算法

对于上述的优化问题，当d函数选取l2-norm时，首先指定一个迭代算法，可以访问梯度∇Sx*。给一个初始向量x0使得Sx*(x0)>0,一个步长序列{ξt}_t≥0,迭代更新为：

其中，ξ是一个正步长，α_t∈[0,1]是一个线性搜索参数被选择来使得Sx*(x_t+1）=0，也就是新的迭代x_t+1会在边界线上，这样选择的原因是后面所用到的梯度方向估计的方法仅在靠近边界时有效。

接下来，论文对上述迭代算法进行一个分析。

先列出一些假设，这些不做介绍，简单列举出来。1.Sx*函数是具有局部 Lipschitz梯度的二次可微的。2.梯度值是远离0的，也就是远离边界的。

其次，对算法的收敛性进行了一个证明。从角度去看:

r(x, x*)= 1的这种情况只会在x在优化为一个固定点的情况下发生。作者通过下面的理论1证明，通过一个适合的步长，更新是可以收敛到这样一个固定点的。

定理1的证明在论文的附录中也给出了。该定理也同时应用于后面选择合适步长的方法中。

2.3 扩展到L∞距离

在l2距离的迭代算法的基础上，针对l∞约束进行一个扩展。

首先，考虑点x在中心位于x 的半径α_t的球面上的l2投影:

基于这个运算式，基于l2的迭代公式可以表示为：

有了这样的表达方式，我们就可以将算法推广到别的约束情况下。可以定义l∞下的投影（这里的定义不太知道怎么来的都是）。**在x的领域内对每一个像素进行clip,使得投影的第i项为**：