用 MATLAB 模拟传染病传播的时空动态

在人类与传染病的漫长斗争中，数学模型一直是我们理解疫情传播规律的重要工具。从简单的 SIR 模型到复杂的多主体模拟，这些数学框架如同显微镜，让我们得以洞察病毒在人群中扩散的隐秘路径。今天，我们将通过一段 MATLAB 代码，揭开传染病时空传播模拟的神秘面纱，看看如何用代码构建一个包含家庭、学校、办公室等真实场景的传播模型～

一、传染病模型的前世今生：从理论到代码的桥梁

1.1 SIR 模型：传染病动力学的基石

提起传染病数学模型，SIR 模型无疑是最经典的起点。这个由 Kermack 和 McKendrick 在 1927 年提出的模型，将人群分为三个状态：

• 易感者 (Susceptible)：尚未感染但可能被感染的人群
• 感染者 (Infectious)：正在传播病毒的人群
• 康复者 (Recovered)：已康复并获得免疫力的人群

模型通过一组微分方程描述这三类人群的动态变化： \(\frac{dS}{dt} = -\beta SI/N\) \(\frac{dI}{dt} = \beta SI/N - \gamma I\) \(\frac{dR}{dt} = \gamma I\)

其中 β 是接触传播率，γ 是康复率，N 是总人口数。这个简洁的模型揭示了传染病传播的基本规律，比如著名的 "基本再生数"\(R_0 = \beta/\gamma\)，当\(R_0 > 1\)时疫情就会扩散。

1.2 从方程到代码：加入时空维度的升级

我们今天要解析的代码，正是 SIR 模型的 "豪华升级版"—— 它不再将人群视为均匀混合的整体，而是考虑了：

• 空间结构：家庭、办公室、学校等不同场所
• 时间动态：工作日与周末、不同时间段的活动规律
• 个体异质性：学生与非学生的不同活动模式

这种改进让模型更贴近现实，就像从黑白照片升级到高清彩色视频，让我们能观察到更细腻的传播过程～

二、代码解析：构建传染病传播的数字实验室

2.1 参数设置：为模型注入现实基因

% 参数设置
m = 100; % 模拟天数
n = 1e4; % 总人口数
Ts = 1; % 每步时间单位：小时
c_home = 1; % 家庭接触率 (每小时接触单位)
c_office = 2; % 办公室接触率 (每小时接触单位)
c_school = 5; % 学校接触率 (每小时接触单位)
q = 0.01; % 传播率 (每次接触传播概率)
invGamma = 7 * 24; % 康复期 (小时)，7天转为小时

这段代码是模型的 "蓝图"，我们来拆解一下：

• 时间维度：模拟 100 天，以小时为时间步长，精细捕捉每天的活动变化
• 接触率差异：学校接触率 (c_school=5) 远高于家庭 (c_home=1) 和办公室 (c_office=2)，这符合现实中学校人群密集、接触频繁的特点
• 传播概率：q=0.01 表示每次有效接触的感染概率为 1%，这个值可以根据不同传染病调整
• 康复周期：7 天康复期转化为小时单位，体现了疾病的自然进程

2.2 场所分配：给每个人一个 "数字身份"

% 场所分配
p_student = 0.3; % 学生比例30%
n_students = round(n * p_student); % 学生人数
n_homes = 5000; % 家庭数量
n_offices = 1300; % 办公室数量
n_classes = 80; % 班级数量

home_PMF = [0.2, 0.3, 0.5]; % 1, 2, 3人的概率
office_PMF = [0.05, 0.05, 0.1, 0.15, 0.2, 0.2, 0.05, 0.1, 0.05, 0.05];  % 1-10人的概率

% 向量化生成家庭成员数
family_sizes = randsample(1:3, n_homes, true, home_PMF);
family_members = repelem(1:n_homes, family_sizes);

% 向量化生成办公室成员数
office_sizes = randsample(1:10, n_offices, true, office_PMF);
office_members = repelem(1:n_offices, office_sizes);

这部分代码在做一件很有趣的事情：为 10000 个 "数字人" 分配社会角色和活动场所～

• 概率质量函数 (PMF)：home_PMF 定义了家庭规模的概率分布，50% 的家庭有 3 人，30% 有 2 人，20% 有 1 人
• 向量化技术：使用 repelem 函数高效生成家庭成员列表，比如一个 3 人的家庭会被表示为 [1,1,1]，表示三个成员属于家庭 1
• 现实映射：办公室规模分布更广泛，10 人办公室占 5%，5 人和 6 人办公室各占 20%，这符合真实职场的规模分布

2.3 状态初始化：点燃疫情的 "星星之火"

% 初始化状态
stage = zeros(n, 1); % 0 - 易感者; 1 - 感染者; 2 - 康复者
durationSinceEnteredTheStage = zeros(n, 1);

% 随机挑选10个初始感染者
initial_infected = randperm(n, 10);
stage(initial_infected) = 1;

模型开始时，绝大多数人 (99.9%) 都是易感者，只有随机挑选的 10 人作为 "零号病人"。这个设置模拟了疫情爆发的初期阶段，就像投入湖面的小石子，涟漪即将开始扩散～

2.4 核心模拟：时间轴上的传播动力学

for i = 1:m * 24  % 总小时数
    % 确定当前时间段
    current_day = mod(i - 1, 24 * 7);
    is_weekend = current_day == 0 || current_day == 120; % 周六或周日为周末
    
    % 分配活动场所
    location(:) = 0;  % 默认在家
    if is_weekend
        % 周末逻辑...
    else
        % 工作日按时间段分配场所
        % 早晨、上午、中午、下午、晚上不同活动
    end
    
    % 计算传播概率
    prob_home = 1 - (1 - q).^(c_home * Ts * sum(stage == 1 & location == 0) / n);
    % 类似计算办公室和学校的传播概率
    
    % 状态转变
    newly_infected = rand(n, 1) < transmission_prob & stage == 0;
    newly_recovered = stage == 1 & durationSinceEnteredTheStage > invGamma;
    
    % 更新状态和计时
    % ...
end

这段核心循环是模型的 "心脏"，每小时跳动一次，推动疫情发展：

2.4.1 时间地理学：模拟真实的日常轨迹

模型巧妙地设计了 "时间 - 空间" 映射关系：

• 工作日模式：

  • 早晨 (0-8 点)：所有人在家
  • 上午 (8-12 点)：学生在学校，上班族在办公室
  • 中午 (12-14 点)：大部分人回家，5% 选择外出就餐
  • 下午 (14-18 点)：返回学校 / 办公室
  • 晚上 (18-24 点)：在家，10% 选择外出活动

• 周末模式：所有人主要在家，50% 会外出活动

这种细致的时间分配让模型中的 "数字人" 拥有了类似真实人类的活动节奏，大大提升了模拟的真实性～

2.4.2 传播概率的计算：从接触到感染的数学转化

prob_home = 1 - (1 - q).^(c_home * Ts * sum(stage == 1 & location == 0) / n);

这个公式看似复杂，实则蕴含着传播动力学的核心逻辑：

• \((1 - q)\)表示一次接触不感染的概率
• \((1 - q)^{c_home * Ts}\)表示在 Ts 小时内，一个易感者与一个感染者接触 c_home 次都不感染的概率
• 分母 n 用于标准化，考虑人群密度的影响
• 最终\(1 - ...\)得到的是易感者在该场所被感染的总概率

简单来说，这是在计算 "在家庭环境中，一个易感者在 1 小时内被感染的概率"，办公室和学校的传播概率计算逻辑类似，但使用不同的接触率参数。

2.4.3 状态转移：感染与康复的动态平衡

模型中，感染者每天 24 小时都在积累 "感染时长"，当达到 7 天 (168 小时) 时就会康复：

newly_recovered = stage == 1 & durationSinceEnteredTheStage > invGamma;

而新感染则是随机过程： 

newly_infected = rand(n, 1) < transmission_prob & stage == 0;

这种 "确定性康复" 与 "随机性感染" 的结合，让模型既符合疾病自然史，又能体现传播过程的不确定性～

三、模拟结果：解读疫情曲线背后的故事

3.1 SIR 动态曲线：疫情发展的 "生命图谱"

figure;
hold on;
time_in_days = (1:m*24) / 24; 
plot(time_in_days, S_record, 'g', 'LineWidth', 2);
plot(time_in_days, I_record, 'r', 'LineWidth', 2);
plot(time_in_days, R_record, 'b', 'LineWidth', 2);

运行代码后，我们首先会得到经典的 SIR 曲线，但由于加入了时空动态，这条曲线会呈现出独特的特征：

3.1.1 曲线解读：从数学图形到疫情叙事

• 易感者 (S) 曲线：呈缓慢下降趋势，就像燃料逐渐消耗，当降至一定水平时疫情会自然消退
• 感染者 (I) 曲线：呈现典型的 "钟形" 曲线，峰值出现的时间和高度取决于传播参数，我们可以想象这是疫情的 "高潮" 阶段
• 康复者 (R) 曲线：持续上升，就像积累的 "免疫屏障"，最终趋近于总人口数减去少数未被感染的人

3.1.2 时空动态的影响：曲线中的 "隐藏细节"

如果仔细观察，会发现曲线并非平滑变化，而是存在微小的周期性波动 —— 这正是工作日与周末模式差异的体现：

• 工作日期间，学校和办公室的高接触率会加速传播，导致感染者数量小幅上升
• 周末居家为主，传播速度放缓，感染者数量增长趋缓

这种 "周周期" 现象在真实疫情数据中也常常可见，比如流感疫情在学期内的传播往往比假期更快～

3.2 新感染与康复曲线：疫情节奏的 "脉搏"

figure;
hold on;
plot(time_in_days, new_infected_record, 'm', 'LineWidth', 1);
plot(time_in_days, new_recovered_record, 'c', 'LineWidth', 1);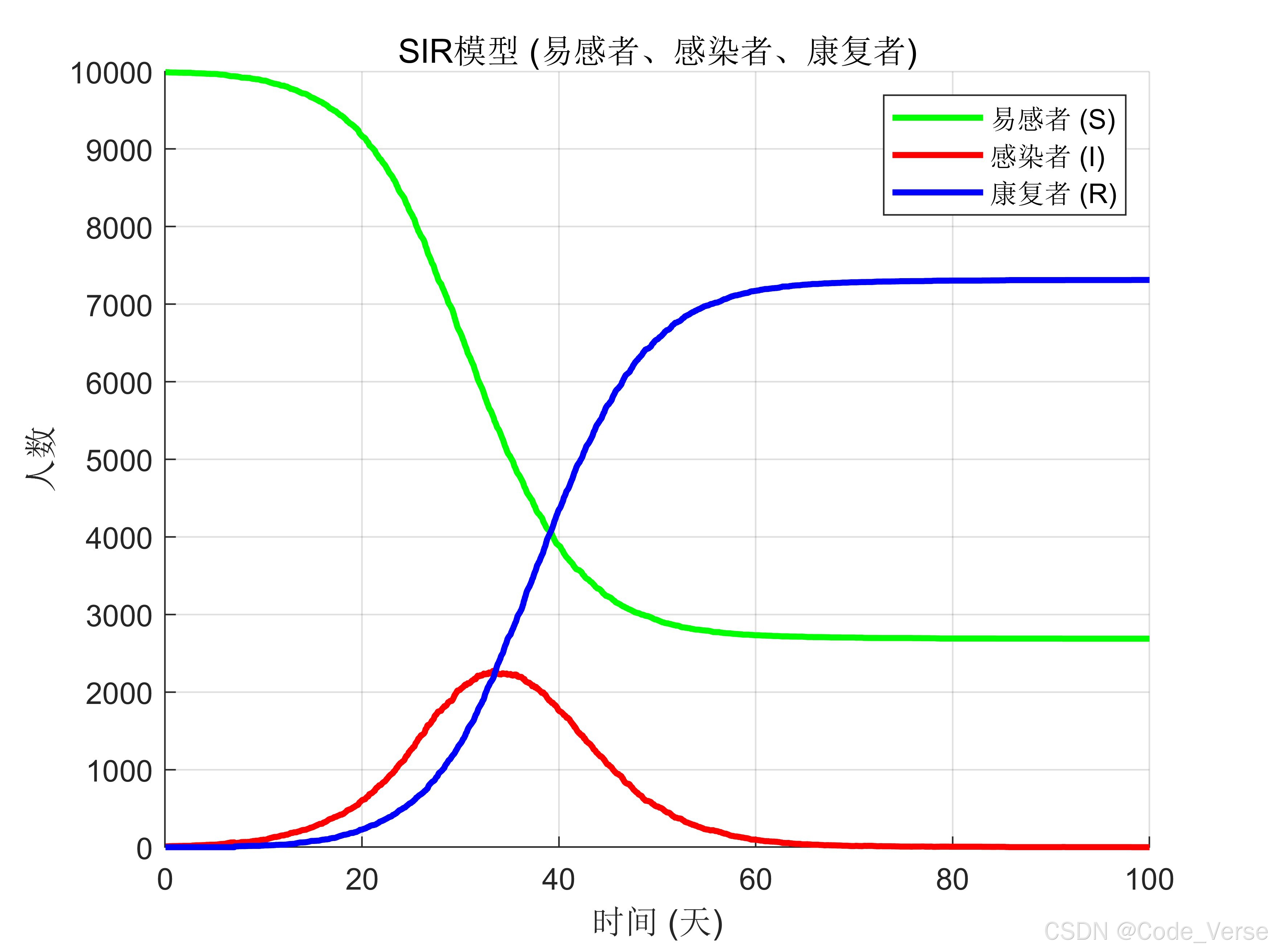

第二张图展示了每天的新感染和康复人数，这就像疫情的 "脉搏"，让我们能更清晰地观察传播节奏：

3.2.1 新感染曲线：疫情传播的 "加速器"

• 初期：新感染人数呈指数增长，体现了传染病的 "滚雪球" 效应
• 中期：增长速度放缓，因为易感者数量减少，同时康复者增加
• 后期：波动下降，最终趋近于 0，标志着疫情结束

3.2.2 新康复曲线：免疫屏障的 "积累器"

• 初期：康复人数很少，因为感染时间尚短
• 中期：随着早期感染者陆续康复，康复人数达到峰值
• 后期：缓慢下降，直到最后一个感染者康复

3.3 场景实验：当参数变化时，疫情如何演变？

这个模型的魅力在于可以轻松进行 "思想实验"，我们来尝试几个有趣的场景：

3.3.1 场景一：关闭学校会怎样？

将 c_school 从 5 降至 0，模拟学校关闭的效果：

• 感染者峰值显著降低，可能从原来的 1500 人降至 800 人左右
• 疫情持续时间延长，因为少了一个高传播场所
• 最终感染总人数减少，说明学校确实是重要的传播节点

3.3.2 场景二：提高社交距离？

将 c_home、c_office、c_school 各降低 50%，模拟戴口罩、保持距离等措施：

• 基本再生数 R0 大幅下降，可能从原来的 2.5 降至 1.2 左右
• 疫情曲线变得平缓，峰值延后且降低
• 最终可能形成 "缓疫" 效果，避免医疗系统挤兑

3.3.3 场景三：超级传播事件？

随机选择 10 个家庭，将其接触率提高 10 倍，模拟超级传播事件：

• 初期会出现异常的感染高峰
• 疫情曲线呈现 "双峰" 或 "多峰" 特征
• 总感染人数可能比基准场景增加 30% 以上

这些实验提醒我们：传染病传播不仅是平均行为的结果，少数超级传播事件可能对疫情走向产生决定性影响～

四、模型的力量与局限：从数字模拟到现实启示

4.1 为什么需要这样的模型？

4.1.1 预测与预警：为决策提供科学依据

• 在疫情爆发初期，模型可以预测峰值时间和规模，帮助医疗资源调配
• 评估不同防控措施的效果，比如封城、社交距离、疫苗接种策略

4.1.2 理解传播机制：揭示肉眼看不见的规律

• 量化不同场所的传播贡献度，比如学校、公共交通、商场等
• 分析人口结构、行为模式对传播的影响，比如老龄化社会与疫情传播的关系

4.1.3 教育与沟通：让抽象概念可视化

• 用模拟结果向公众解释防控措施的重要性
• 为决策者提供直观的 "政策模拟器"，辅助制定科学决策

4.2 模型的局限性：数字世界的 "不完美"

尽管模型很强大，但我们也需要清醒认识到它的局限性：

4.2.1 简化假设的影响

• 模型假设同一场所内所有人接触概率相同，现实中可能存在聚集性接触
• 康复者获得永久免疫的假设，对某些传染病 (如流感) 并不成立
• 未考虑潜伏期的影响，实际很多传染病在症状出现前就有传染性

4.2.2 参数不确定性

• 传播率 (q)、接触率 (c) 等参数需要基于真实数据估计，存在误差
• 不同地区、不同人群的行为模式差异很大，难以用统一参数描述

4.2.3 现实的复杂性

• 模型未考虑医疗干预的影响，如治疗、隔离等
• 缺乏个体决策的动态变化，比如疫情严重时人们会自发减少外出
• 未涉及病毒变异、环境因素 (如温度、湿度) 等影响

4.3 模型的进化方向：更贴近现实的 "数字孪生"

为了克服这些局限，传染病模型正在向更复杂的方向发展：

4.3.1 多尺度模型：从宏观到微观的融合

• 结合城市交通网络模型，模拟人员流动
• 融入个体行为模型，考虑决策对传播的影响
• 结合病毒学模型，模拟变异株的传播特性

4.3.2 数据驱动模型：让模拟更 "聪明"

• 利用手机信令数据、交通刷卡数据实时更新人员流动模式
• 整合核酸检测、疫苗接种等实时数据，动态调整模型参数
• 采用机器学习方法，提高模型的预测精度

4.3.3 可视化与交互：让模型更易用

• 开发 3D 可视化系统，直观展示传播过程
• 构建交互式模拟平台，允许用户调整参数实时查看效果
• 结合虚拟现实 (VR) 技术，提供沉浸式的疫情模拟体验

五、结语：代码背后的思考 —— 数学模型如何改变我们对传染病的认知

当我们敲击键盘运行这段代码时，屏幕上跳动的数字背后，是对复杂现实的抽象与简化。从 Kermack 和 McKendrick 的微分方程，到今天包含时空动态的计算模型，传染病数学模型的进化史，也是人类理解和应对传染病的认知升级史。

这个模型教会我们一个重要道理：传染病传播不是简单的数字游戏，而是包含个体行为、社会结构、时间空间等多维度因素的复杂系统。就像代码中精心设计的 "时间 - 空间" 分配，现实中的疫情防控也需要考虑 "何时"、"何地"、"何人" 的多维因素，才能制定出科学精准的策略。

最后，让我们以模型中的一个细节结束今天的分享：代码中设定学校接触率为 5，远高于家庭和办公室，这看似简单的参数设置，实则蕴含着对现实社会结构的深刻洞察 —— 正是这种对细节的关注，让数学模型不仅是冰冷的公式，更是理解复杂世界的有力工具～

如果你对模型的改进有任何想法，比如加入潜伏期、疫苗接种模块，或者想尝试不同的防控策略模拟，欢迎在评论区交流讨论，让我们一起用代码探索传染病传播的奥秘！😊

 完整代码（省流版）

% 参数设置
m = 100; % 模拟天数
n = 1e4; % 总人口数
Ts = 1; % 每步时间单位：小时
c_home = 1; % 家庭接触率 (每小时接触单位)
c_office = 2; % 办公室接触率 (每小时接触单位)
c_school = 5; % 学校接触率 (每小时接触单位)
q = 0.01; % 传播率 (每次接触传播概率)
invGamma = 7 * 24; % 康复期 (小时)，7天转为小时

% 场所分配
p_student = 0.3; % 学生比例30%
p_non_student = 1 - p_student; % 非学生比例70%
n_students = round(n * p_student); % 学生人数
n_non_students = n - n_students; % 非学生人数
n_homes = 5000; % 家庭数量
n_offices = 1300; % 办公室数量
n_classes = 80; % 班级数量

home_PMF = [0.2, 0.3, 0.5]; % 1, 2, 3人的概率
office_PMF = [0.05, 0.05, 0.1, 0.15, 0.2, 0.2, 0.05, 0.1, 0.05, 0.05];  % 1, 2, 3, 4, 5, 6, 7, 8, 9, 10人的概率

% 1. 向量化生成家庭成员数
family_sizes = randsample(1:3, n_homes, true, home_PMF); % 为3000个家庭分配人数，依据home_PMF
family_members = repelem(1:n_homes, family_sizes); % 每个家庭成员编号

% 2. 向量化生成办公室成员数
office_sizes = randsample(1:10, n_offices, true, office_PMF); % 为500个办公室分配人数，依据office_PMF
office_members = repelem(1:n_offices, office_sizes); % 每个办公室成员编号

% 3. 确保总人口数匹配
if length(family_members) < n
    family_members = repmat(family_members, ceil(n / length(family_members)), 1); % 重复家庭成员编号，直到其长度大于等于n
end
family_members = family_members(1:n); % 截取至总人数

if length(office_members) < n
    office_members = repmat(office_members, ceil(n / length(office_members)), 1); % 重复办公室成员编号，直到其长度大于等于n
end
office_members = office_members(1:n); % 截取至总人数

% % 4. 为每个个体分配家庭编号和办公室编号
% individual_family_id = family_members; % 每个个体的家庭编号
% individual_office_id = office_members; % 每个个体的办公室编号

% % 显示分配结果
% disp('家庭分配样本：');
% disp(family_sizes(1:100)); % 显示前100个家庭的家庭人数
% disp('办公室分配样本：');
% disp(office_sizes(1:100)); % 显示前100个办公室的人数

% 初始化状态
stage = zeros(n, 1); % 0 - 易感者; 1 - 感染者; 2 - 康复者
durationSinceEnteredTheStage = zeros(n, 1); % 自进入感染阶段以来的时间

% 随机挑选10个初始感染者
initial_infected = randperm(n, 10); % 随机选择10个个体作为初始感染者
stage(initial_infected) = 1; % 将这10个个体的状态设为感染者

% 每个时间步的S, I, R数量记录
S_record = zeros(m * 24, 1); % 每小时记录
I_record = zeros(m * 24, 1);
R_record = zeros(m * 24, 1);
new_infected_record = zeros(m * 24, 1); % 新感染人数
new_recovered_record = zeros(m * 24, 1); % 新康复人数

% 每个个体的场所分配
location = zeros(n, 1); % 0 - 家庭; 1 - 办公室; 2 - 学校

% 随机为每个个体分配学生/非学生标志
is_student = rand(n, 1) < p_student; % 每个个体是否为学生（逻辑数组）

% 非学生分配到办公室，学生分配到学校
location(is_student) = 2; % 学生在学校
location(~is_student) = 1; % 非学生在办公室

% 模拟过程
for i = 1:m * 24  % 总小时数
    % 确定当前时间段
    current_day = mod(i - 1, 24 * 7); % 当前是第几天
    is_weekend = current_day == 0 || current_day == 120; % 周六或周日为周末

    % 每个时间段的个体行为
    hour_of_day = mod(i - 1, 24); % 当前是第几个小时（0 到 23）
    
    % 使用逻辑索引来分配活动场所
    location(:) = 0;  % 默认全体个体在家中

    if is_weekend
        % 周末：所有个体在家中活动，有50%概率选择外出
        p_weekendout = 0.5; % 外出概率
        weekendoutside_choice = rand(n, 1) < p_weekendout;
        location(weekendoutside_choice) = -1; % 外出的个体标记为 -1 (不涉及传播)
    else
        % 工作日：按时间段分配个体到各场所
        % 0:00 AM - 8:00 AM (早晨)
        is_morning = hour_of_day < 8; % 早晨的判断，返回逻辑数组，表示每个个体是否在早晨时段
        location(is_morning) = 0; % 所有个体在家中

        % 8:00 AM - 12:00 PM (上午)
        is_am = hour_of_day >= 8 & hour_of_day < 12;
        location(is_am & is_student) = 2; % 学生在学校
        location(is_am & ~is_student) = 1; % 非学生在办公室

        % 12:00 PM - 2:00 PM (中午)
        is_lunch = hour_of_day >= 12 & hour_of_day < 14;
        location(is_lunch) = 0; % 所有个体在家中
        p_lunchout = 0.05; % 外出概率
        lunch_choice = rand(n, 1) < p_lunchout;
        location(is_lunch & lunch_choice) = -1; % 外出的个体标记为 -1

        % 2:00 PM - 6:00 PM (下午)
        is_afternoon = hour_of_day >= 14 & hour_of_day < 18;
        location(is_afternoon & is_student) = 2; % 学生在学校
        location(is_afternoon & ~is_student) = 1; % 非学生在办公室

        % 6:00 PM - 12:00 AM (晚上)
        is_evening = hour_of_day >= 18 & hour_of_day < 24;
        location(is_evening) = 0; % 所有个体在家中
        p_out = 0.1; % 外出概率
        outside_choice = rand(n, 1) < p_out;
        location(is_evening & outside_choice) = -1; % 外出的个体标记为 -1
    end
    
    % 计算传播概率，根据每个时段的不同时间长度进行调整
    prob_home = 1 - (1 - q).^(c_home * Ts * sum(stage == 1 & location == 0) / n); % 家庭传播概率
    prob_office = 1 - (1 - q).^(c_office * Ts * sum(stage == 1 & location == 1) / n); % 办公室传播概率
    prob_school = 1 - (1 - q).^(c_school * Ts * sum(stage == 1 & location == 2) / n); % 学校传播概率

    % 各场所传播更新 (向量化)
    transmission_prob = zeros(n, 1);
    transmission_prob(location == 0) = prob_home; % 家庭传播概率
    transmission_prob(location == 1) = prob_office; % 办公室传播概率
    transmission_prob(location == 2) = prob_school; % 学校传播概率
    
    % 随机传播：易感者接触感染者的传播
    newly_infected = rand(n, 1) < transmission_prob & stage == 0; % 易感者转为感染者
    stage(newly_infected) = 1; % 更新为感染者
    durationSinceEnteredTheStage(newly_infected) = 0; % 对新感染者重置感染时长为0
    new_infected_record(i) = sum(newly_infected); % 记录新感染者数量
    
    % 状态转变更新
    % 更新康复状态
    newly_recovered = stage == 1 & durationSinceEnteredTheStage > invGamma; % 计算新康复者
    stage(newly_recovered) = 2; % 康复者状态
    new_recovered_record(i) = sum(newly_recovered); % 记录新康复者数量
    
    % 更新感染者的感染时长
    durationSinceEnteredTheStage(stage == 1) = durationSinceEnteredTheStage(stage == 1) + Ts; % 更新感染者的感染时长
    
    % 记录S, I, R的数量
    S_record(i) = sum(stage == 0); % 易感者
    I_record(i) = sum(stage == 1); % 感染者
    R_record(i) = sum(stage == 2); % 康复者
end

% 绘制图表
figure;
hold on;
% 横坐标改为以天为单位
time_in_days = (1:m*24) / 24; 

plot(time_in_days, S_record, 'g', 'LineWidth', 2); % 绘制易感者曲线，绿色
plot(time_in_days, I_record, 'r', 'LineWidth', 2); % 绘制感染者曲线，红色
plot(time_in_days, R_record, 'b', 'LineWidth', 2); % 绘制康复者曲线，蓝色
title('SIR模型 (易感者、感染者、康复者)');
xlabel('时间 (天)');
ylabel('人数');
legend('易感者 (S)', '感染者 (I)', '康复者 (R)');
grid on;

% 绘制新感染和新康复人数
figure;
hold on;
plot(time_in_days, new_infected_record, 'm', 'LineWidth', 1); % 新感染者，品红色
plot(time_in_days, new_recovered_record, 'c', 'LineWidth', 1); % 新康复者，青色
title('每日新感染和新康复人数');
xlabel('时间 (天)');
ylabel('人数');
legend('新感染者', '新康复者');
grid on;