目录
5.亥姆霍兹定理
6.源和场的关系
7.麦克斯韦方程组
如何深入浅出地讲解麦克斯韦方程组? - 知乎 (zhihu.com) https://www.zhihu.com/question/36766702
https://www.zhihu.com/question/36766702
5.亥姆霍兹定理
回顾上节课
矢量场性质=散度+旋度
标量场性质=梯度
矢量场存在:
无旋场散度不处处为0
无散场旋度不处处为0
矢量场有源:
散度(通量)>0,发散源;<0,汇聚源
旋度(环量,涡旋场):旋涡源

通过高斯定理,斯托克斯定理分别由微分到积分:

6.源和场的关系

其中,一个场有散度,称为“有势场”,意思是散度不为0。
最常见的矢量源——电流。
7.麦克斯韦方程组

D:电位移矢量。
中间的演化是斯托克斯定理和高斯定理。
7.1 积分形式

(1)高斯电场定律描述了电场的起源(静电)
通过一个闭合曲面的电通量跟曲面内包含电荷总量是成正比的,电荷量越大,通过这个任意闭合曲面的电通量就越大,反之亦然。这就是麦克斯韦方程组的第一个方程——高斯电场定律的核心思想。其中,enc:闭合曲面包含的电荷总量。
(2)高斯磁定律描述了磁场的起源(静磁)
进去的磁通量跟出来的磁通量相等,那么最后这个闭合曲面包含的总磁通量就恒为0了。这就是麦克斯韦方程组的第二个方程——高斯磁场定律的核心思想:闭合曲面包含的磁通量恒为0。截至目前,没有找到磁单极子。
(1)(2)为什么这种高斯XX定律能够成立?为什么通过任意闭合曲面的某种通量会刚好是某种量的一个量度?
原因还在它们的“平方反比”上。因为电场强度和磁感应强度都是跟距离的平方成反比,而表面积是跟距离的平方正比,所以你前者减小多少,后者就增加多少。那么,如果有一个量的表示形式是前者和后者的乘积,那么它的总量就会保持不变。而通量刚好就是XX强度和表面积的乘积,所以电通量、磁通量就都会有这样的性质。
(3)法拉第电磁感应定律描述了变化的磁场如何产生电场(磁生电)
只要通过曲面(我们可以把闭合回路当作一个曲面)的磁通量发生了改变,回路中就会产生电流,而且磁通量变化得越快,这个电流就越大。曲面的磁通量变化率=感生电场环流。麦克斯韦方程组的第三个方程——法拉第定律的最后表述就是这样的:曲面的磁通量变化率等于感生电场的环流。负号:维持稳定。
法拉第定律的第二种形式,与微分形式对应更好。认为只有磁场变化导致的磁通量变化才是法拉第定律,前面导体运动导致的磁通量变化只是通量法则。后面这个只是把那个变化率从原来的针对整个磁通量移到了只针对磁场强度B(因为B不是只跟时间t有关,还可以跟其它的量有关,所以我们这里必须使用对时间的偏导的符号∂B/∂t),也就是说它只考虑变化磁场导致的磁通量变化。
(4)安培环路定律描述了磁场的环流与相应回路所围绕的电流之间的关系(电生磁)
安培环路定理只限定曲面的边界,并不管你曲面的其它地方,于是我们就看到这两个相同边界的曲面会得到完全不同的结论,这就只能说明:安培环路定理错了,或者至少它并不完善。(一个曲面不包裹,一个曲面包裹电容的电极板,结论相反,详情见014_如何深入浅出地讲解麦克斯韦方程组? - 知乎 (zhihu.com))
电场强度越来越大,那么通过这个曲面的电通量也就越来越大。因此,我们可以看到虽然没有电流通过这个曲面,但是通过这个曲面的电通量却发生了改变。这样,我们就可以非常合理地把“变化的电通量”这一项也添加到产生磁场的原因里。因为这项工作是麦克斯韦完成的,所以添加之后的新公式就是麦克斯韦方程组的第四个方程——安培-麦克斯韦定律。预言电磁波的存在,变化的磁生电变化的电生磁。

高斯电场定律说穿过闭合曲面的电通量正比于这个曲面包含的电荷量。
高斯磁场定律说穿过闭合曲面的磁通量恒等于0。
法拉第定律说穿过曲面的磁通量的变化率等于感生电场的环流。
安培-麦克斯韦定律说穿过曲面的电通量的变化率和曲面包含的电流等于感生磁场的环流。
如果一个曲面是闭合的,那么通过它的通量就是曲面里面某种东西的量度。因为自然界存在独立的电荷,所以高斯电场定律的右边就是电荷量的大小,因为我们还没有发现磁单极子,所以高斯磁场定律右边就是0。
如果一个曲面不是闭合的,那么它就无法包住什么,就不能成为某种荷的量度。但是,一个曲面如果不是闭合的,它就有边界,于是我们就可以看到这个非闭合曲面的通量变化会在它的边界感生出某种旋涡状的场,这种场可以用环流来描述。因而,我们就看到了:如果这个非闭合曲面的磁通量改变了,就会在这个曲面的边界感生出电场,这就是法拉第定律;如果这个非闭合曲面的电通量改变了,就会在这个曲面的边界感生出磁场,这就是安培-麦克斯韦定律的内容。
7.2 微分形式

(1)全电流定律,推广的安培环路定理
,某一点感生磁场的旋度▽×B等于电流密度J和电场变化率∂E/∂t两项的叠加。
▽算子也有3种作用方式:
1、▽算子作用在一个标量函数z上:▽z。它表示函数z的梯度,表示函数z变化最快的方向。
2、▽算子跟一个矢量函数E点乘:▽·E。这就表示E的散度。
3、▽算子跟一个矢量函数E叉乘:▽×E。它叫E的旋度。
(2)法拉第电磁感应定律
,某一点电场的旋度等于磁感应强度的变化率
▽算子以叉乘的方式作用在电场E上,我们就得到了电场E的旋度▽×E,旋度的另一种定义就是无穷小非闭合曲面的环流和这个曲面的面积之比。
旋度的定义是无穷小曲面的环流和面积的比值
(3)高斯磁场定理
磁场的散度处处为0。
点乘是不满足结合律的,也就是说没有(OA·OB)·OC=OA·(OB·OC),为什么?因为两个矢量点乘之后的结果是一个标量,你再让一个标量去点乘另一个矢量压根就没有意义,点乘是两个矢量之间的运算。
(4)高斯电场定理
无穷小曲面的通量和▽·这两种散度的定义方式各有所长,比如我们在判断某一点的散度是否为零的时候,我用第一个定义,去看看包含这个点的无穷小曲面的通量是不是为零就行了。如果这一点有电荷,那么这个无穷小曲面的电通量肯定就不为零,它的散度也就不为零;如果这个无穷小曲面没有包含电荷,那这一点的散度一定为0,这就是高斯电场定律的微分方程想要告诉我们的东西。但是,如果你要计算这一点的散度是多少,那还是乖乖的拿起▽·去计算吧。
对于一个点电荷产生的电场,只有电荷所在的点的散度不为0,其他地方的散度都为0。
【散度误区】很多初学者认为只要看起来发散的东西就是有散度的,然后我们通过分析知道这是不对的。一个点电荷产生静电场,只要在电荷处散度不为零的,在其他地方,虽然看起来是散开的,其实它的散度是零。如果我们放一个非常轻的橡皮筋在上面,除了电荷所在处,其它地方这个橡皮筋是不会被撑开的(即便会被冲走),所以其他地方的散度都为零。
【旋度误区】在旋度这里,一个变换的磁场会产生一个旋涡状的电场,在旋涡的中心,在磁场变化的这个中心点这里,它的旋度肯定是不为零的。但是,在其它地方呢?从公式上看,其它地方的旋度一定为零,为什么?因为其他地方并没有变化的磁场啊,所以按照法拉第定律的微分形式,没有变化的磁场的地方的电场的旋度肯定是0。
高斯电场定律说电场的散度跟这点的电荷密度成正比。
高斯磁场定律说磁场的散度处处为0。
法拉第定律说感生电场的旋度等于磁感应强度的变化率。
安培-麦克斯韦定律说感生磁场的旋度等于电流密度和电场强度变化率之和。
通量和环流是定义在曲面上的,而散度和旋度是定义在一个点上的。我们可以说通过通过一个曲面的通量或者沿曲面边界的环流,但是当我们在说散度和旋度的时候,我们都是在说一个点的散度和旋度。
7.3 微分形式演化到积分形式:散度定理、斯托克斯定理
其中,斯托克斯定理描述的是线积分和面积分之间的关系,散度定理描述的是面积分和体积分之间的关系。环量:旋度穿过一个面的通量;波动:电磁场的基本运动形态

7.4 物理意义


麦克斯韦方程组是不是相互独立的?
结论:不是完全独立,可以由两组(静电+静磁,或者电生磁+磁生电)导出其余的(电生磁+磁生电,或者静电+静磁)。
推导:以电生磁推导静电为例
(1)旋度场必是无散场,所以结果为。
(2)电流发散出去,作一个面,包起来;因为发散,电荷守恒,里面是减少,故添负号。
麦克斯韦方程-1-基础综述 - 知乎 (zhihu.com) https://zhuanlan.zhihu.com/p/339143878麦克斯韦方程组积分与微分形式的讨论 - 知乎 (zhihu.com)
https://zhuanlan.zhihu.com/p/339143878麦克斯韦方程组积分与微分形式的讨论 - 知乎 (zhihu.com) https://zhuanlan.zhihu.com/p/682325737
https://zhuanlan.zhihu.com/p/682325737








 本文详细介绍了麦克斯韦方程组,包括其微分和积分形式,以及与散度、旋度、电荷和电流的关系。内容涵盖了亥姆霍兹定理、源和场的相互作用,以及电磁场的物理意义,如时变电场和磁场的激发原理。
本文详细介绍了麦克斯韦方程组,包括其微分和积分形式,以及与散度、旋度、电荷和电流的关系。内容涵盖了亥姆霍兹定理、源和场的相互作用,以及电磁场的物理意义,如时变电场和磁场的激发原理。

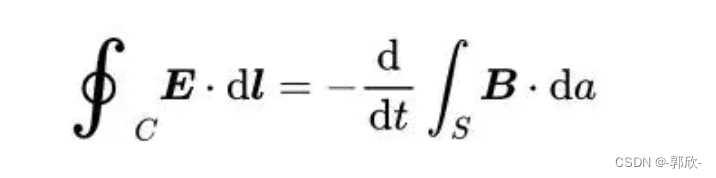
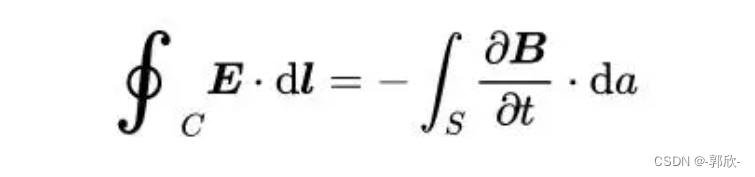





















 1803
1803

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








