hdoj Saving Beans 3037 （Lucas定理入门）

Saving Beans

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3482    Accepted Submission(s): 1326

Problem Description

Although winter is far away, squirrels have to work day and night to save beans. They need plenty of food to get through those long cold days. After some time the squirrel family thinks that they have to solve a problem. They suppose that they will save beans in n different trees. However, since the food is not sufficient nowadays, they will get no more than m beans. They want to know that how many ways there are to save no more than m beans (they are the same) in n trees.

Now they turn to you for help, you should give them the answer. The result may be extremely huge; you should output the result modulo p, because squirrels can’t recognize large numbers.

Input

The first line contains one integer T, means the number of cases.

Then followed T lines, each line contains three integers n, m, p, means that squirrels will save no more than m same beans in n different trees, 1 <= n, m <= 1000000000, 1 < p < 100000 and p is guaranteed to be a prime.

Output

You should output the answer modulo p.

Sample Input

  
  

   
   2
1 2 5
2 1 5
  
  

Sample Output

  
  

   
   3
3

   
   

    
    

     
     Hint
    
    
Hint

For sample 1, squirrels will put no more than 2 beans in one tree. Since trees are different, we can label them as 1, 2 … and so on. 
The 3 ways are: put no beans, put 1 bean in tree 1 and put 2 beans in tree 1. For sample 2, the 3 ways are:
 put no beans, put 1 bean in tree 1 and put 1 bean in tree 2.

   
   
   
   

    
    //题意：
   
   
   
   

    
    有n棵树，m个种子，现在要把m个种子放到这n棵树上（也可以不放），问有几种放法。
//思路：
因为可以不放（比较难弄），所以我们可以转化一下，假设有m个虚树，如果没放在实树上，那么就证明放到了虚树上
这样就转化成将m个种子放到n+m个树上，也就是C(n+m,m)种情况，那么用Lucas定理就可以解了。
   
   
   
   

    
    //这里简单介绍一下Lucas定理
   
   
   
   

    
    
对于C(n, m) mod p。这里的n，m，p（p为素数）都很大的情况。就不能再用C(n, m) = C(n - 1，m) + C(n - 1, m - 1)的公式递推了。
    
    
这里用到Lusac定理
    
    
For non-negative integers m and n and a prime p, the following congruence relation holds:
    
    

     
     

      
      
     
     
    
    
    
    
where
    
    

     
     

      
      
     
     
    
    
    
    
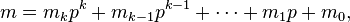
and
    
    

     
     

      
      
     
     
    
    
    
    
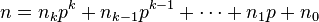
are the base p expansions of m and n respectively.
    
    
 
    
    
 对于单独的C(ni, mi) mod p，已知C(n, m) mod p = n!/(m!(n - m)!) mod p。显然除法取模，这里要用到m!(n-m)!的逆元。
    
    
根据费马小定理：
    
    
已知(a, p) = 1，则 ap-1 ≡ 1 (mod p),  所以 a*ap-2 ≡ 1 (mod p)。
    
    
也就是 (m!(n-m)!)的逆元为 (m!(n-m)!)p-2 ；
   
   
   
   

    
    
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define ll long long
using namespace std;
int n,m,p;
ll ksm(ll x,ll y)//快速幂 
{
	ll ans=1;
	while(y)
	{
		if(y&1)
			ans=(ans*x)%p;
		x*=x;
		x%=p;
		y>>=1;
	}
	return ans%p;
}
ll C(int n,int m)
{
	int i;
	ll sum1=1,sum2=1;
	for(i=1;i<=m;i++)
	{
		sum1=(sum1*(n-i+1))%p;
		sum2=(sum2*i)%p;
	}
	sum1=(sum1*ksm(sum2,p-2))%p;
	return sum1;
}
void solve(int n,int m)//Lucas定理 
{
	ll ans=1;
	while(n&&m&&ans)
	{
		ans=(ans*C(n%p,m%p))%p;
		n/=p;
		m/=p;
	}
	printf("%lld\n",ans);
}
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d%d%d",&n,&m,&p);		
		solve(n+m,m);
	}
	return 0;
}
    
    
//大神总结的博客：
    
    http://m.blog.csdn.net/blog/wilson1068/39228737