2 单变量线性回归(Linear Regression with One Variable)
2.1 模型表示(Model Representation)
- 房价预测训练集
| Size in f e e t 2 feet^2 feet2 ( x x x) | Price ($) in 1000’s( y y y) |
| ---------------------- | ------------------------- |
| 2104 | 460 |
| 1416 | 232 |
| 1534 | 315 |
| 852 | 178 |
| … | … |
房价预测训练集中,同时给出了输入 x x x 和输出结果 y y y,即给出了人为标注的**”正确结果“**,且预测的量是连续的,属于监督学习中的回归问题。
- 问题解决模型
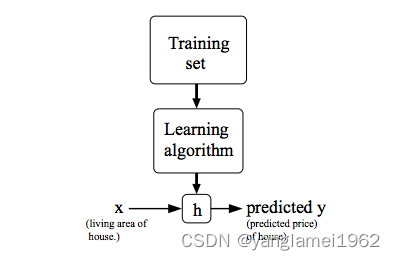
其中 h h h 代表结果函数,也称为假设(hypothesis) 。假设函数根据输入(房屋的面积),给出预测结果输出(房屋的价格),即是一个 X → Y X\to Y X→Y 的映射。
h θ ( x ) = θ 0 + θ 1 x h_\theta(x)=\theta_0+\theta_1x hθ(x)=θ0+θ1x,为解决房价问题的一种可行表达式。
x x x: 特征/输入变量。
上式中, θ \theta θ 为参数, θ \theta θ 的变化才决定了输出结果,不同以往,这里的 x x x 被我们视作已知(不论是数据集还是预测时的输入),所以怎样解得 θ \theta θ 以更好地拟合数据,成了求解该问题的最终问题。
单变量,即只有一个特征(如例子中房屋的面积这个特征)。
2.2 代价函数(Cost Function)
李航《统计学习方法》一书中,损失函数与代价函数两者为同一概念,未作细分区别,全书没有和《深度学习》一书一样混用,而是统一使用损失函数来指代这类类似概念。
吴恩达(Andrew Ng)老师在其公开课中对两者做了细分。如果要听他的课做作业,不细分这两个概念是会被打小手扣分的!这也可能是因为老师发现了业内混用的乱象,想要治一治吧。
损失函数(Loss/Error Function): 计算单个样本的误差。link
代价函数(Cost Function): 计算整个训练集所有损失函数之和的平均值
综合考虑,本笔记对两者概念进行细分,若有所谬误,欢迎指正。
我们的目的在于求解预测结果 h h h 最接近于实际结果 y y y 时 θ \theta θ 的取值,则问题可表达为求解 ∑ i = 0 m ( h θ ( x ( i ) ) − y ( i ) ) \sum\limits_{i=0}^{m}(h_\theta(x^{(i)})-y^{(i)}) i=0∑m(hθ(x(i))−y(i)) 的最小值。
m m m: 训练集中的样本总数
y y y: 目标变量/输出变量
( x , y ) \left(x, y\right) (x,y): 训练集中的实例
( x ( i ) , y ( i ) ) \left(x^{\left(i\right)},y^{\left(i\right)}\right) (x(i),y(i)): 训练集中的第 i i i 个样本实例
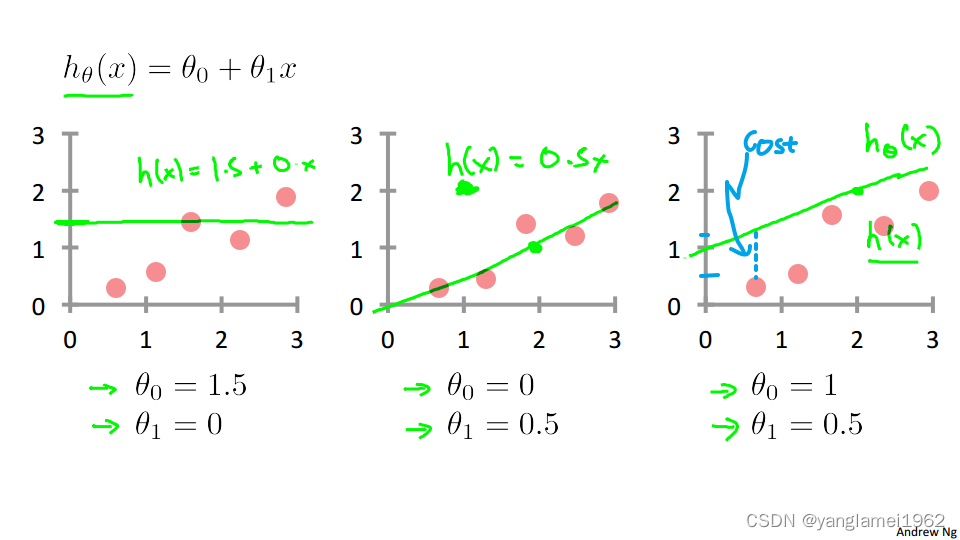
上图展示了当 θ \theta θ 取不同值时, h θ ( x ) h_\theta\left(x\right) hθ(x) 对数据集的拟合情况,蓝色虚线部分代表建模误差(预测结果与实际结果之间的误差),我们的目标就是最小化所有误差之和。
为了求解最小值,引入代价函数(Cost Function)概念,用于度量建模误差。考虑到要计算最小值,应用二次函数对求和式建模,即应用统计学中的平方损失函数(最小二乘法):
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( y ^ i − y i ) 2 = 1 2 m ∑ i = 1 m ( h θ ( x i ) − y i ) 2 J(\theta_0,\theta_1)=\dfrac{1}{2m}\displaystyle\sum_{i=1}^m\left(\hat{y}_{i}-y_{i} \right)^2=\dfrac{1}{2m}\displaystyle\sum_{i=1}^m\left(h_\theta(x_{i})-y_{i}\right)^2 J(θ0,θ1)=2m1i=1∑m(y^i−yi)2=2m1i=1∑m(hθ(xi)−yi)2
y ^ \hat{y} y^: y y y 的预测值
系数 1 2 \frac{1}{2} 21 存在与否都不会影响结果,这里是为了在应用梯度下降时便于求解,平方的导数会抵消掉 1 2 \frac{1}{2} 21 。
讨论到这里,我们的问题就转化成了求解 J ( θ 0 , θ 1 ) J\left( \theta_0, \theta_1 \right) J(θ0,θ1) 的最小值。
2.3 代价函数 - 直观理解1(Cost Function - Intuition I)
根据上节视频,列出如下定义:
- 假设函数(Hypothesis): h θ ( x ) = θ 0 + θ 1 x h_\theta(x)=\theta_0+\theta_1x hθ(x)=θ0+θ1x
- 参数(Parameters): θ 0 , θ 1 \theta_0, \theta_1 θ0,θ1
- 代价函数(Cost Function): J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( \theta_0, \theta_1 \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}}} J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
- 目标(Goal): minimize θ 0 , θ 1 J ( θ 0 , θ 1 ) \underset{\theta_0, \theta_1}{\text{minimize}} J \left(\theta_0, \theta_1 \right) θ0,θ1minimizeJ(θ0,θ1)
为了直观理解代价函数到底是在做什么,先假设 θ 1 = 0 \theta_1 = 0 θ1=0,并假设训练集有三个数据,分别为 ( 1 , 1 ) , ( 2 , 2 ) , ( 3 , 3 ) \left(1, 1\right), \left(2, 2\right), \left(3, 3\right) (1,1),(2,2),(3,3),这样在平面坐标系中绘制出 h θ ( x ) h_\theta\left(x\right) hθ(x) ,并分析 J ( θ 0 , θ 1 ) J\left(\theta_0, \theta_1\right) J(θ0,θ1) 的变化。
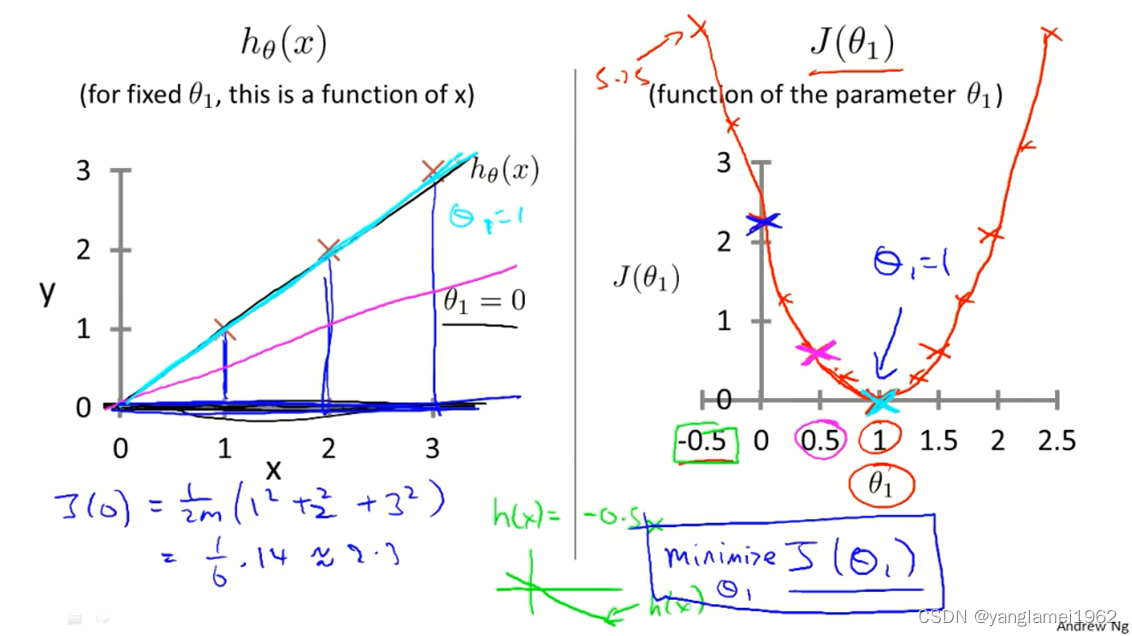
右图 J ( θ 0 , θ 1 ) J\left(\theta_0, \theta_1\right) J(θ0,θ1) 随着 θ 1 \theta_1 θ1 的变化而变化,可见**当 θ 1 = 1 \theta_1 = 1 θ1=1 时, J ( θ 0 , θ 1 ) = 0 J\left(\theta_0, \theta_1 \right) = 0 J(θ0,θ1)=0,取得最小值,**对应于左图青色直线,即函数 h h h 拟合程度最好的情况。
2.4 代价函数 - 直观理解2(Cost Function - Intuition II)
注:该部分由于涉及到了多变量成像,可能较难理解,要求只需要理解上节内容即可,该节如果不能较好理解可跳过。
给定数据集:
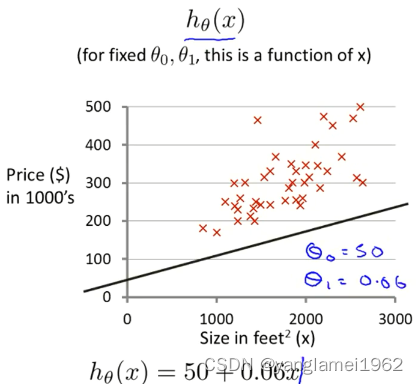
参数在 θ 0 \theta_0 θ0 不恒为 0 0 0 时代价函数 J ( θ ) J\left(\theta\right) J(θ) 关于 θ 0 , θ 1 \theta_0, \theta_1 θ0,θ1 的3-D图像,图像中的高度为代价函数的值。
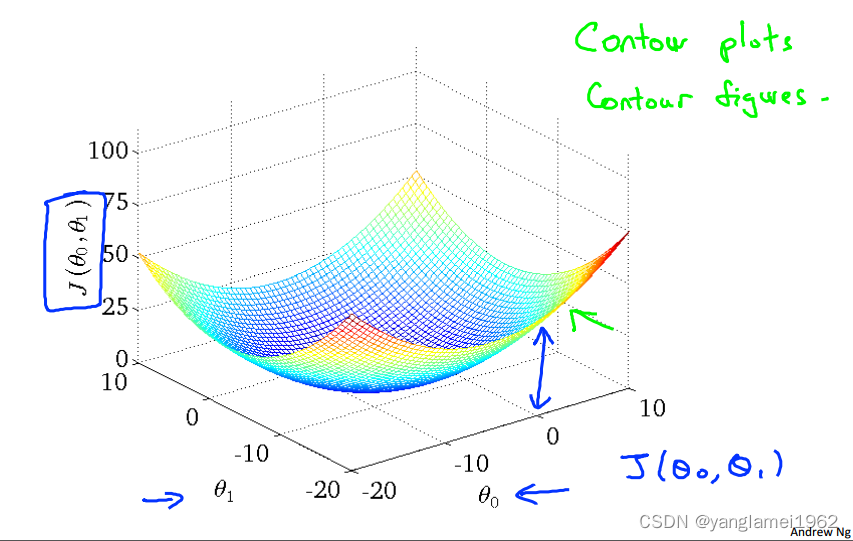
由于3-D图形不便于标注,所以将3-D图形转换为轮廓图(contour plot),下面用轮廓图(下图中的右图)来作直观理解,其中相同颜色的一个圈代表着同一高度(同一 J ( θ ) J\left(\theta\right) J(θ) 值)。
θ 0 = 360 , θ 1 = 0 \theta_0 = 360, \theta_1 =0 θ0=360,θ1=0 时:
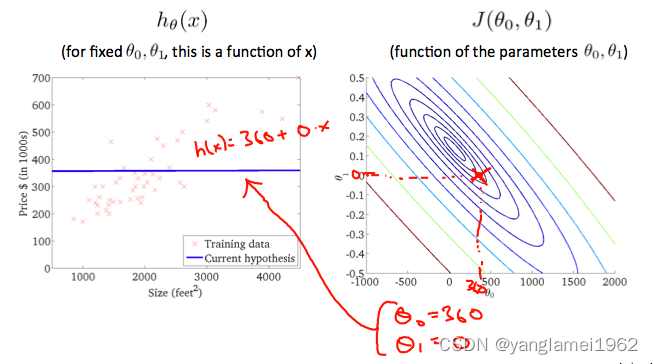
大概在 θ 0 = 0.12 , θ 1 = 250 \theta_0 = 0.12, \theta_1 =250 θ0=0.12,θ1=250 时:
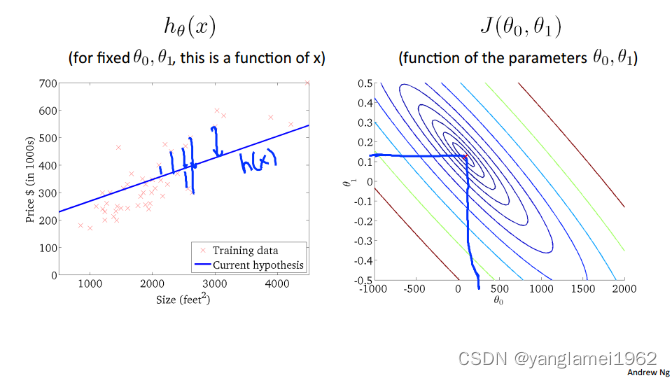
上图中最中心的点(红点),近乎为图像中的最低点,也即代价函数的最小值,此时对应 h θ ( x ) h_\theta\left(x\right) hθ(x) 对数据的拟合情况如左图所示,嗯,一看就拟合的很不错,预测应该比较精准啦。
2.5 梯度下降(Gradient Descent)
在特征量很大的情况下,即便是借用计算机来生成图像,人工的方法也很难读出 J ( θ ) J\left(\theta\right) J(θ) 的最小值,并且大多数情况无法进行可视化,故引入梯度下降(Gradient Descent)方法,让计算机自动找出最小化代价函数时对应的 θ \theta θ 值。
梯度下降背后的思想是:开始时,我们随机选择一个参数组合 ( θ 0 , θ 1 , . . . . . . , θ n ) \left( {\theta_{0}},{\theta_{1}},......,{\theta_{n}} \right) (θ0,θ1,......,θn)即起始点,计算代价函数,然后寻找下一个能使得代价函数下降最多的参数组合。不断迭代,直到找到一个局部最小值(local minimum),由于下降的情况只考虑当前参数组合周围的情况,所以无法确定当前的局部最小值是否就是全局最小值(global minimum),不同的初始参数组合,可能会产生不同的局部最小值。
下图根据不同的起始点,产生了两个不同的局部最小值。
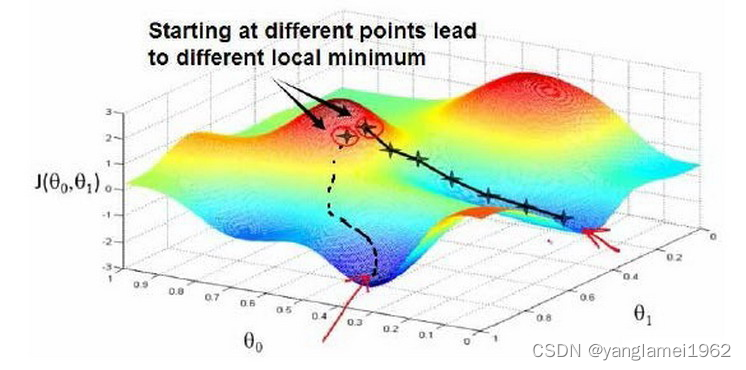
视频中举了下山的例子,即我们在山顶上的某个位置,为了下山,就不断地看一下周围下一步往哪走下山比较快,然后就迈出那一步,一直重复,直到我们到达山下的某一处陆地。
梯度下降公式:
Repeat until convergence: { θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) } \begin{align*} & \text{Repeat until convergence:} \; \lbrace \\ &{{\theta }_{j}}:={{\theta }_{j}}-\alpha \frac{\partial }{\partial {{\theta }_{j}}}J\left( {\theta_{0}},{\theta_{1}} \right) \\ \rbrace \end{align*} }Repeat until convergence:{θj:=θj−α∂θj∂J(θ0,θ1)
θ j {\theta }_{j} θj: 第 j j j 个特征参数
”:=“: 赋值操作符
α \alpha α: 学习速率(learning rate), α > 0 \alpha > 0 α>0
∂ ∂ θ j J ( θ 0 , θ 1 ) \frac{\partial }{\partial {{\theta }_{j}}}J\left( \theta_0, \theta_1 \right) ∂θj∂J(θ0,θ1): J ( θ 0 , θ 1 ) J\left( \theta_0, \theta_1 \right) J(θ0,θ1) 的偏导
公式中,学习速率决定了参数值变化的速率即”走多少距离“,而偏导这部分决定了下降的方向即”下一步往哪里“走(当然实际上的走多少距离是由偏导值给出的,学习速率起到调整后决定的作用),收敛处的局部最小值又叫做极小值,即”陆地“。

注意,在计算时要批量更新 θ \theta θ 值,即如上图中的左图所示,否则结果上会有所出入,原因不做细究。
2.6 梯度下降直观理解(Gradient Descent Intuition)
该节探讨 θ 1 \theta_1 θ1 的梯度下降更新过程,即 θ 1 : = θ 1 − α d d θ 1 J ( θ 1 ) \theta_1 := \theta_1 - \alpha\frac{d}{d\theta_1}J\left(\theta_1\right) θ1:=θ1−αdθ1dJ(θ1),此处为了数学定义上的精确性,用的是 d d θ 1 J ( θ 1 ) \frac{d}{d\theta_1}J\left(\theta_1\right) dθ1dJ(θ1),如果不熟悉微积分学,就把它视作之前的 ∂ ∂ θ \frac{\partial}{\partial\theta} ∂θ∂ 即可。
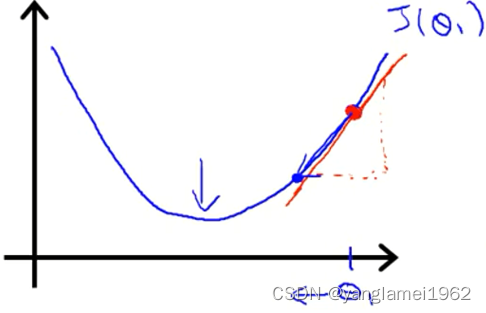
把红点定为初始点,切于初始点的红色直线的斜率,表示了函数 J ( θ ) J\left(\theta\right) J(θ) 在初始点处有正斜率,也就是说它有正导数,则根据梯度下降公式 , θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) {{\theta }_{j}}:={{\theta }_{j}}-\alpha \frac{\partial }{\partial {{\theta }_{j}}}J\left( \theta_0, \theta_1 \right) θj:=θj−α∂θj∂J(θ0,θ1) 右边的结果是一个正值,即 θ 1 \theta_1 θ1 会向左边移动。这样不断重复,直到收敛(达到局部最小值,即斜率为0)。
初始 θ \theta θ 值(初始点)是任意的,若初始点恰好就在极小值点处,梯度下降算法将什么也不做( θ 1 : = θ 1 − α ∗ 0 \theta_1 := \theta_1 - \alpha*0 θ1:=θ1−α∗0)。
不熟悉斜率的话,就当斜率的值等于图中三角形的高度除以水平长度好啦,精确地求斜率的方法是求导。
对于学习速率 α \alpha α,需要选取一个合适的值才能使得梯度下降算法运行良好。
- 学习速率过小图示:
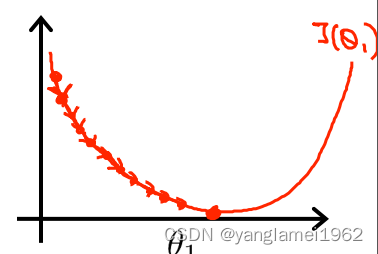
收敛的太慢,需要更多次的迭代。
- 学习速率过大图示:

可能越过最低点,甚至导致无法收敛。
学习速率只需选定即可,不需要在运行梯度下降算法的时候进行动态改变,随着斜率越来越接近于0,代价函数的变化幅度会越来越小,直到收敛到局部极小值。
如图,品红色点为初始点,代价函数随着迭代的进行,变化的幅度越来越小。
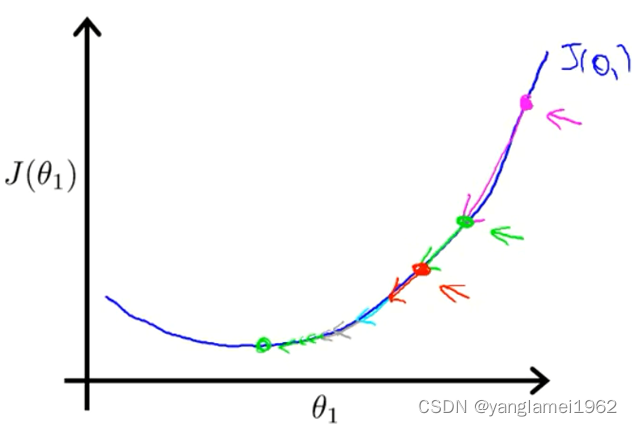
最后,梯度下降不止可以用于线性回归中的代价函数,还通用于最小化其他的代价函数。
2.7 线性回归中的梯度下降(Gradient Descent For Linear Regression)
线性回归模型
- h θ ( x ) = θ 0 + θ 1 x h_\theta(x)=\theta_0+\theta_1x hθ(x)=θ0+θ1x
- J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( \theta_0, \theta_1 \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}}} J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
梯度下降算法
Repeat until convergence:
{
θ
j
:
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
0
,
θ
1
)
}
\begin{align*} & \text{Repeat until convergence:} \; \lbrace \\ &{{\theta }_{j}}:={{\theta }_{j}}-\alpha \frac{\partial }{\partial {{\theta }_{j}}}J\left( {\theta_{0}},{\theta_{1}} \right) \\ \rbrace \end{align*}
}Repeat until convergence:{θj:=θj−α∂θj∂J(θ0,θ1)
直接将线性回归模型公式代入梯度下降公式可得出公式

当
j
=
0
,
j
=
1
j = 0, j = 1
j=0,j=1 时,线性回归中代价函数求导的推导过程:
∂
∂
θ
j
J
(
θ
1
,
θ
2
)
=
∂
∂
θ
j
(
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
)
=
(
1
2
m
∗
2
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
)
∗
∂
∂
θ
j
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
=
(
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
)
∗
∂
∂
θ
j
(
θ
0
x
0
(
i
)
+
θ
1
x
1
(
i
)
−
y
(
i
)
)
\begin{align*} \frac{\partial}{\partial\theta_j} J(\theta_1, \theta_2)&=\frac{\partial}{\partial\theta_j} \left(\frac{1}{2m}\sum\limits_{i=1}^{m}{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}} \right)\\ &=\left(\frac{1}{2m}*2\sum\limits_{i=1}^{m}{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}} \right)*\frac{\partial}{\partial\theta_j}{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}}\\ &=\left(\frac{1}{m}\sum\limits_{i=1}^{m}{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}} \right)*\frac{\partial}{\partial\theta_j}{{\left(\theta_0{x_0^{(i)}} + \theta_1{x_1^{(i)}}-{{y}^{(i)}} \right)}} \end{align*}
∂θj∂J(θ1,θ2)=∂θj∂(2m1i=1∑m(hθ(x(i))−y(i))2)=(2m1∗2i=1∑m(hθ(x(i))−y(i)))∗∂θj∂(hθ(x(i))−y(i))=(m1i=1∑m(hθ(x(i))−y(i)))∗∂θj∂(θ0x0(i)+θ1x1(i)−y(i))
所以当 j = 0 j = 0 j=0 时:
∂ ∂ θ 0 J ( θ ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ∗ x 0 ( i ) \frac{\partial}{\partial\theta_0} J(\theta)=\frac{1}{m}\sum\limits_{i=1}^{m}{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}} *x_0^{(i)} ∂θ0∂J(θ)=m1i=1∑m(hθ(x(i))−y(i))∗x0(i)
所以当 j = 1 j = 1 j=1 时:
∂
∂
θ
1
J
(
θ
)
=
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
∗
x
1
(
i
)
\frac{\partial}{\partial\theta_1} J(\theta)=\frac{1}{m}\sum\limits_{i=1}^{m}{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}} *x_1^{(i)}
∂θ1∂J(θ)=m1i=1∑m(hθ(x(i))−y(i))∗x1(i)
上文中所提到的梯度下降,都为批量梯度下降(Batch Gradient Descent),即每次计算都使用所有的数据集
(
∑
i
=
1
m
)
\left(\sum\limits_{i=1}^{m}\right)
(i=1∑m) 更新。
由于线性回归函数呈现碗状,且只有一个全局的最优值,所以函数一定总会收敛到全局最小值(学习速率不可过大)。同时,函数 J J J 被称为凸二次函数,而线性回归函数求解最小值问题属于凸函数优化问题。
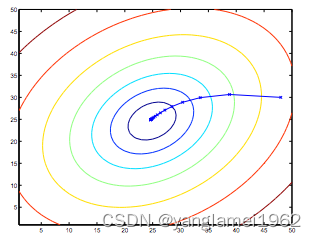
另外,使用循环求解,代码较为冗余,后面会讲到如何使用**向量化(Vectorization)**来简化代码并优化计算,使梯度下降运行的更快更好。























 1186
1186











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










