目录
高斯分布的分类
一维高斯分布
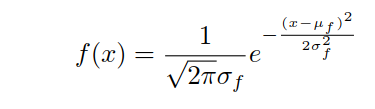
循环高斯分布
冯·米塞斯分布(von Mises distribution)指一种圆上连续概率分布模型,它也被称作循环正态分布(circular normal distribution)。
多维高斯分布
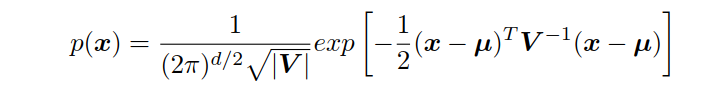
混合高斯分布(GMM 多个高斯核,归一化)
GMM模型,有k个核,归一化之后,可得到多峰分布,在参数估计的时候,由于不知道数据属于哪个核,需要进行EM估计;换句话说存在隐式变量;
复合型(卷积操作)
- Z=X+Y
- Z=X-Y
- Z=XY
- Z=X/Y

密度函数乘积形式
两个概率密度函数相乘的形式,主要用于贝叶斯估计,后验分布∝ \propto∝先验*似然;
注:高斯分布的共轭先验分布式高斯分布。
应用: https://blog.csdn.net/lmm6895071/article/details/79771606
高斯变量基础
高斯分布

概率密度函数
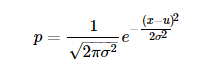
性质

复高斯分布
若复高斯分布Z=X+iY, 且满足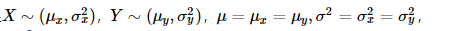
则有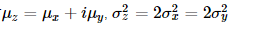
概率密度函数
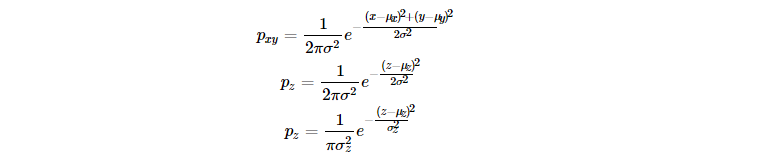
注:复高斯随机变量的密度函数,分母已经没有根号
应用
零均值循环对称复高斯随机变量
特殊的,当μ=μx=μy=0时,Z称为零均值循环对称复高斯随机变量(zero mean circle symmetric complex gaussian,ZMCSCG),σ2称为每个实数维度上的方差。
以上分析得出复高斯随机变量与每一实数维度高斯随机变量的关系
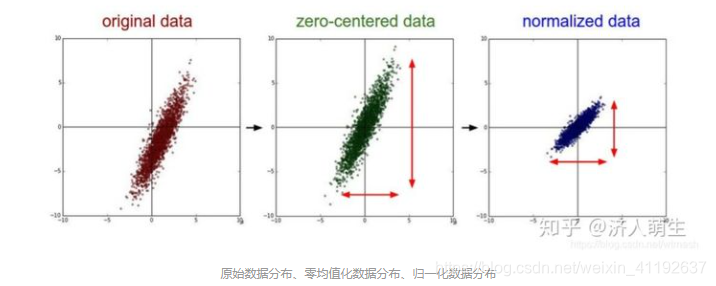
零均值化
将每个像素的值减去训练集上所有像素值的平均值,比如已计算得所有像素点的平均值为128,所以减去128后,现在的像素值域即为[-128,127],即满足均值为零。
卡方分布
设X1,X2,X3,…,i.i.d∼N(0,1), 令 , 则X是服从自由度为n的χ2分布,记为X∼χ2(n)
, 则X是服从自由度为n的χ2分布,记为X∼χ2(n)
卡方分布为特殊的Gamma分布,服从参数为G(n/2,1/2)

注意:
复高斯随机变量概率表达式的分母
复高斯随机变量模平方的分布与卡方分布、指数分布、Gamma分布之间的关系
补充
归一化、标准化、零均值化核心思想:平移+缩放
归一化

【作用】将某个特征的值映射到[0,1]之间,消除量纲对最终结果的影响,使不同的特征具有可比性,使得原本可能分布相差较大的特征对模型有相同权重的影响,提升模型的收敛速度,深度学习中数据归一化可以防止模型梯度爆炸。
标准化

【作用】将原值减去均值后除以标准差,使得得到的特征满足均值为0,标准差为1的正态分布,使得原本可能分布相差较大的特征对模型有相同权重的影响。举个例子,在KNN中,需要计算待分类点与所有实例点的距离。假设每个实例(instance)由n个features构成。如果选用的距离度量为欧式距离,数据预先没有经过归一化,那些绝对值大的features在欧式距离计算的时候起了决定性作用
从经验上说,标准化后,让不同维度之间的特征在数值上有一定比较性,得出的参数值的大小可以反应出不同特征对样本label的贡献度,可以大大提高分类器的准确性。
【二者比较】具体应该选择归一化还是标准化呢,如果把所有维度的变量一视同仁,
①在计算距离中发挥相同的作用,应该选择标准化,标准化更适合现代嘈杂大数据场景。
②如果想保留原始数据中由标准差所反映的潜在权重关系,或数据不符合正态分布时,选择归一化。
参考https://zhuanlan.zhihu.com/p/183591302 https://www.cnblogs.com/zwwangssd/p/12540280.html
加性高斯白噪声
高斯是指概率分布是正态函数,白噪声是指他的二阶矩不相关,一阶矩为常数,是指先后信号在时间上的相关性。高斯白噪声是研究信道加性噪声的理想模型,通信中的主要噪声源—热噪声就属于这类噪声。
高斯函数、高斯积分和正态分布
正态分布是高斯概率分布。高斯概率分布是反映中心极限定理原理的函数,该定理指出当随机样本足够大时,总体样本将趋向于期望值并且远离期望值的值将不太频繁地出现。高斯积分是高斯函数在整条实数线上的定积分。这三个主题,高斯函数、高斯积分和高斯概率分布是这样交织在一起的,所以我认为最好尝试一次性解决这三个主题(但是我错了,这是本篇文章的不同主题)。
本篇文章我们首先将研究高斯函数的一般定义是什么,然后将看一下高斯积分,其结果对于确定正态分布的归一化常数是非常必要的。最后我们将使用收集的信息理解,推导出正态分布方程。
首先,让我们了解高斯函数实际上是什么。高斯函数是将指数函数 exp(x) 与凹二次函数(例如 -(ax^2+bx+c) 或 -(ax^2+bx) 或只是-ax^2组成的函数。结果是一系列呈现“钟形曲线”的形状的函数。

两个高斯函数的图。第一个高斯(绿色)的λ=1和a=1。第二个(橙色)λ=2和a=1.5。两个函数都不是标准化的。也就是说,曲线下的面积不等于1。
大多数人都熟悉这类曲线是因为它们在概率和统计中被广泛使用,尤其是作为正态分布随机变量的概率密度函数。在这些情况下,函数具有的系数和参数既可以缩放“钟形”的振幅,改变其标准差(宽度),又可以平移平均值,所有这一切都是在曲线下的面积进行归一化(缩放钟形,使曲线下的面积总是等于1)的同时进行的。结果是一个高斯函数包含了一大堆的参数来影响这些结果。

如果将其认为是均值 = μ 且标准差 = σ 的正态分布方程。将其与高斯 λ exp(-ax^2) 的一般形式进行比较,我们可以看到:
- (x - μ)^2表示的是均值μ如何在x轴上左右平移图像,这就是均值要做的。如果μ=0,那么图的中心为0。
- σ2,是一个测量随机变量的方差,也就是说数据是如何分散的,当我们使用a=1/(2σ2)缩小或扩大图形时,我们希望同时缩放图形使用λ=1/√2πσ^2。这样图下的面积才能保持为1。
参考























 1492
1492











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








