转自:http://blog.csdn.net/smartempire/article/details/21406005
这篇文章主要介绍人脸识别经典方法的第一篇,后续会有其他方法更新。特征脸方法基本是将人脸识别推向真正可用的第一种方法,了解一下还是很有必要的。特征脸用到的理论基础PCA在另一篇博客里:特征脸(Eigenface)理论基础-PCA(主成分分析法) 。本文的参考资料附在最后了
步骤一:获取包含M张人脸图像的集合S。在我们的例子里有25张人脸图像(虽然是25个不同人的人脸的图像,但是看着怎么不像呢,难道我有脸盲症么),如下图所示哦。每张图像可以转换成一个N维的向量(是的,没错,一个像素一个像素的排成一行就好了,至于是横着还是竖着获取原图像的像素,随你自己,只要前后统一就可以),然后把这M个向量放到一个集合S里,如下式所示。
步骤二:在获取到人脸向量集合S后,计算得到平均图像Ψ ,至于怎么计算平均图像,公式在下面。就是把集合S里面的向量遍历一遍进行累加,然后取平均值。得到的这个Ψ 其实还挺有意思的,Ψ 其实也是一个N维向量,如果再把它还原回图像的形式的话,可以得到如下的“平均脸”,是的没错,还他妈的挺帅啊。那如果你想看一下某计算机学院男生平均下来都长得什么样子,用上面的方法就可以了。
步骤三:计算每张图像和平均图像的差值Φ ,就是用S集合里的每个元素减去步骤二中的平均值。(目的是为了找出本张脸的独特特征用于区别其他脸)
步骤四:找到M个正交的单位向量un ,这些单位向量其实是用来描述Φ (步骤三中的差值)分布的。un 里面的第k(k=1,2,3...M)个向量uk 是通过下式计算的,
当这个λk(原文里取了个名字叫特征值)取最小的值时,uk 基本就确定了。补充一下,刚才也说了,这M个向量是相互正交而且是单位长度的,所以啦,uk 还要满足下式:
上面的等式使得uk 为单位正交向量。计算上面的uk 其实就是计算如下协方差矩阵的特征向量:
其中
对于一个NxN(比如100x100)维的图像来说,上述直接计算其特征向量计算量实在是太大了(协方差矩阵可以达到10000x10000),所以有了如下的简单计算。
步骤四另解:如果训练图像的数量小于图像的维数比如(M<N^2),那么起作用的特征向量只有M-1个而不是N^2个(因为其他的特征向量对应的特征值为0),所以求解特征向量我们只需要求解一个NxN的矩阵。(?????没懂)这个矩阵就是步骤四中的AAT ,我们可以设该矩阵为L,那么L的第m行n列的元素可以表示为:
一旦我们找到了L矩阵的M个特征向量vl,那么协方差矩阵的特征向量ul就可以表示为:
这些特征向量如果还原成像素排列的话,其实还蛮像人脸的,所以称之为特征脸(如下图)。图里有二十五个特征脸,数量上和训练图像相等只是巧合。有论文表明一般的应用40个特征脸已经足够了。论文Eigenface for recognition里只用了7个特征脸来表明实验。
步骤五:识别人脸。(首先要用特征脸来表征这张新的人脸)OK,终于到这步了,别绕晕啦,上面几步是为了对人脸进行降维找到表征人脸的合适向量的。首先考虑一张新的人脸,我们可以用特征脸对其进行标示(像T的那个代表新的人脸,减号后面的字母是平均脸):
其中k=1,2...M,对于第k个特征脸uk,上式可以计算其对应的权重,M个权重可以构成一个向量:
perfect,这就是求得的特征脸对人脸的表示了!
那如何对人脸进行识别呢,看下式:
其中Ω代表要判别的人脸,Ωk代表训练集内的某个人脸,两者都是通过特征脸的权重来表示的。式子是对两者求欧式距离,当距离小于阈值时说明要判别的脸和训练集内的第k个脸是同一个人的。当遍历所有训练集都大于阈值时,根据距离值的大小又可分为是新的人脸或者不是人脸的两种情况。根据训练集的不同,阈值设定并不是固定的。
后续会有对PCA理论的补充^_^.已补充理论:特征脸(Eigenface)理论基础-PCA(主成分分析法)
参考资料:
1、Eigenface for Recognition:http://www.cs.ucsb.edu/~mturk/Papers/jcn.pdf
2、特征脸维基百科:http://zh.wikipedia.org/wiki/%E7%89%B9%E5%BE%81%E8%84%B8
3、Eigenface_tutorial:http://www.pages.drexel.edu/~sis26/Eigenface%20Tutorial.htm








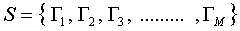

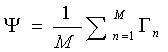

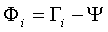
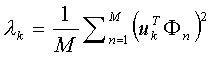
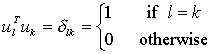
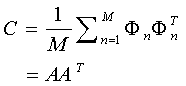
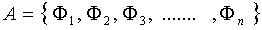
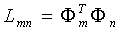


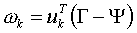
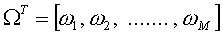
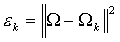














 834
834

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








