FedCorr: Multi-Stage Federated Learning for Label Noise Correction

在现实世界的FL实现中，客户端数据可能有标签噪声，而不同的客户端可能有不同程度的标签噪声水平。虽然在中心式学习中存在方法来处理标签噪声，但这些方法在FL场景下中对异构标签噪声表现不佳， 这是因为FL的客户端数据集较少与数据隐私要求。
在本文中提出了FedCorr，一个通用的多阶段框架来处理FL中的异构标签噪声，而无需对本地客户的噪声模型做任何假设，同时仍然可以保护客户数据隐私。

现有的方法虽然检测有噪声的客户端，在有噪声的客户端上也没有进一步修正标签的机制；
或者可以减轻有噪声标签的影响，虽然有通过一个辅助数据集的帮助来减轻噪声标签的影响，但没有任何直接的标签校正。

还有种方法是在客户机和服务器之间交换特征质心，这种质心的交换可能会导致隐私问题，因为质心可能被用作逆向工程的一部分，以揭示有关原始本地数据的重要信息。

Contributions

1. 提出了一个通用的多阶段FL框架FedCorr来解决数据异构性的问题，其中异构性指的是本地标签的质量与本地数据的统计信息
2. 提出了一个简单的用于生成联邦合成标签噪声与多样化的用户数据划分框架。
3. 通过LID分数识别噪声客户，并通过每个样本损失识别噪声标签。我们还提出了一个基于估计的局部噪声水平的自适应局部近端正则化项。
4. 证明了对于IID和非IID数据分区，IID在具有不同噪声水平的多个数据集上优于最先进的FL方法。

Related Work

Local intrinsic dimension (LID)

这部分介绍了LID的定义说明与极大似然估计方法；
LID是一种对数据集内在维度的衡量的工具。其关键的基本思想是，对于每个数据点，邻近数据点的数量会随着邻近半径的增加而增加，而相应的增长率就能代表 "本地 "维度。
LID建立在这个想法的基础上，通过几何思想，当一个m维欧几里得球的体积按比例增长时，它的半径按r因子成比例增长.具体来说，当我们有两个体积为v1,v2，半径为r1,r2时，我们可以计算m如下：

假设我们有一个由Rn中的向量组成的数据集,我们将把这个数据集视为从n-变量分布D中抽取的样本,设FYx (t)为Yx的累积分布函数,给定r > 0和从D中抽取的样本点x，定义距离r处x的LID为：

假设它存在，即假设FYx (t)是正的，并且在t = r处连续可微。x处的LID被定义为极限 :$LIDx=limr\to 0LIDx(r)$
直观地说，x处的LID是包含x的维度的近似，它将拟合“最”适合x的凸度分布D。

LID估计：

Proposed Method

3.1 Preliminaries

这篇工作提出的框架分为3个部分:

1. 预处理：通过LID分数从采样的一小部分客户机中识别出带有噪声的客户机，然后将识别出的噪声样本与全局模型的预测标签进行重新标记。同时还识别了每一个客户的噪声水平。
2. 微调；在相对干净的客户端以一定比例来调整模型，并使用调优后的模型来进一步修正剩余客户端的样本。
3. 常规训练；我们通过通常的FL方法，在第二阶段结束时使用修正后的标签来训练模型（FedAvg)。

Data partition
在本工作中同时考虑IID和非IID异构数据分区。
对于IID：每个类型的数据均匀的分布在各个客户端中；
对于非IID: 首先生成一个N*M指示器矩阵$\Phi$，其中每个条目${\Phi }_{ij}$表示客户端i的本地数据集是否包含类$j$, 每个Φij都应以固定的概率p从伯努利分布中采样；
对于每1个1≤ j ≤M，设${\upsilon }_j$为Φ的第j列中的条目之和，这等于本地数据集包含类$j$的客户端数量。设$q_j$为长度为υj的向量，从具有公共参数${\alpha }_{Dir}$ > 0的对称狄利克雷分布中采样。使用$q_j$作为概率向量，然后我们在其中随机分配样本类$j$到这些${\upsilon }_j$客户端中。

噪声模型
为简单起见，这项工作只考虑了与实例无关的标签噪声;该框架有两个参数$\rho$和$\tau$，其中$\rho$表示系统噪声水平（有噪声客户端的比率），$\tau$表示有噪声客户端的噪声水平的下界。每个客户端都有一个成为有噪声客户端的概率$\rho$，在这种情况下，这个有噪声客户端的局部噪声水平是通过从均匀分布U（$\tau$，1）中采样来随机确定的。
从下图可以发现，文章认为的noise是有噪声的客户中对应数量的数据被打上从所有类别M中随机抽取的错误标签。

LID scores for local models
这篇工作的做法是对于每个客户端，对其计算
，这个值越大，说明本地数据集中噪声越多，随着本地模型f（·）每一轮的更新，相应的LID分数将发生相应的变化。
直观地说，一个训练良好的模型的预测向量，在一个干净的数据集上训练，将对应于M类别，围绕M个可能的one-hot向量聚集类。然而，随着更多的标签噪声被添加到干净的数据集上，一个噪声样本的预测向量会倾向于向其他簇移动，不同的噪声样本的向不同方向位移，因此，每个热向量附近的预测向量将变得“更扩散”，平均跨越更高维的空间。

T1、T2、T3分别对应文章提出的三个阶段对应的迭代轮次。

3.2 Federated pre-processing stage

FedCorr从预处理阶段开始，该阶段迭代地评估每个客户端的数据集的质量，并重新标记识别出的噪声样本。这个预处理阶段不同于传统联邦学习体现在以下几个方面：

1. 所有的客户机都将参与到每次迭代中来
2. 在损失函数中添加一个自适应的局部近端项，并使用混合数据增强
3. 每个客户端在本地训练后计算其LID分数和每个样本的交叉熵损失，并将其LID分数与本地模型更新一起发送到服务器

Client iteration and fraction scheduling
每个迭代都是由通信轮组织的，类似于通常的FL，但有两个关键的区别：一小部分客户端被选择而不需要替换。且保证每次迭代结束 ，所有的客户都参与其中。
这样做的原因是因为虽然选取大部分的客户进行训练有助于提高训练速度，甚至在凸损失函数中可以达到线性加速，但是在non-iid场景下不会带来更加好的效果，在这种场景下小部分客户参与将产生与局部模型偏离较少的聚合模型；
于是文章想结合以上两种策略的优点，于是提出以下方案：
具体来说，我们在预处理阶段使用一小部分客户，但是不进行替换，在后两个阶段使用典型的更大部分，且进行替换。

Mixup and local proximal regularization
这部分介绍了预处理阶段每个客户端本地的损失函数；

mixup是一种数据增强技术，
（大型深度神经网络功能强大，但也会表现出一些不良行为，如记忆和对对抗性示例的敏感性，从本质上讲，mixup在成对的例子及其标签的凸组合上训练神经网络。
通过这样做，mixup使神经网络正则化，以支持训练示例之间的简单线性行为）
有利于表示样本之间的线性关系，并且已被证明对标记噪声表现出很强的鲁棒性.
mixup生成新的样本（˜x、y˜）作为随机选择的样本对（xx、yi）和（xj、yj）的凸组合; 其中˜x=λxi+（1−λ）xj，y˜=λyi+（1−λ）yj给出，其中λ∼Beta（α，α），和α∈（0，∞）.（在实验中使用了α = 1）
直观地说，如果客户端的数据集与其他本地数据集有较大的差异，那么相应的局部模型就会更容易偏离全局模型，从而造成局部近端项的值更大的损失。

Identification of noisy clients and noisy samples.
为了解决非均匀标签噪声的挑战，文章在预处理阶段迭代识别和重新标记噪声样本。
在这个预处理阶段的每个迭代中，所有客户端都将参与(但每个round只会选取一小部分客户），每个客户端将计算其当前本地模型的LID分数和每个样本损失。具体来说，当在t轮中选择客户端k时，客户端k利用本地数据进行训练，然后计算LID分数。
在一轮迭代t结束时，我们将执行以下三个步骤：

1. 服务器首先在所有N个客户端的累积LID分数上计算一个高斯混合模型（GMM）。
2. 每个有噪声的客户端k∈Sn在本地对本地数据集Dk中的所有样本的每个样本损失值计算一个新的GMM。
3. 每个有噪声的客户端k∈Sn通过使用全局模型的预测标签作为新的标签，对有噪声的样本进行重新标记。

解决overcorrection的方法:
这种部分重新标记由一个重新标记比率π和一个置信度阈值θ控制。选取前k个样本的交叉熵损失最大的数据，然后只有当样本预测向量（global model给出）的最大值超过θ时，才重新标记样本。

Why do we use cumulative LID scores in step 1?
作者发现噪音水平较大的客户往往有较大的LID分数。此外，在训练期间，干净的客户和嘈杂的客户之间的LID分数的重叠也会增加。这种增加可能是由于两个原因： (1) 模型可能会逐渐过拟合 (2) 在每次迭代后对识别出的噪声样本进行校正，从而使干净的客户与低噪音水平的客户不太容易区分。
因此，累积LID分数（即过去所有迭代中LID分数的总和）是一个区分噪声客户端的更好的指标。
图3为使用LID评分与累积LID评分的比较。此外，图3中底部的两个图显示，累积LID得分与局部噪声水平有较强的线性关系.

3.3 Federated finetuning stage

这一步的目标是在T2轮中在相对干净的客户端上调整全局模型，并进一步重新标记剩余的噪声客户端。其中，$\kappa$是用于根据估计的局部噪声水平来选择相对干净的客户端的阈值，这一轮会选择低于该阈值的客户参与全局模型调整。
在微调阶段结束时，我们重新标记剩余的噪声客户端，与预处理阶段的校正过程类似，我们使用global model的预测向量，使用相同的置信阈值$\theta$来控制要重新标记的样本子集；

3.4 Federated usual training stage

在最后一个阶段，我们通过在所有客户上通常的FL（FedAvg）在T3轮上训练全局模型，这一轮也会使用在前两个训练阶段修正的标签。

4 Experiment

其中clothing1M是一个带有噪声标签的大规模真实世界数据集。它包含了来自14个不同的与布相关的类的1M幅图像。由于标签是由卖家提供的图像周围文本制作的，大部分令人困惑的类别（如针织服和毛衣）会被错误地标记。

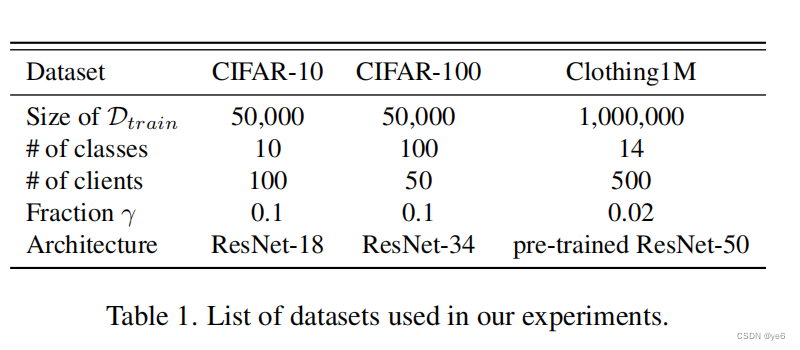
实验分为两组：
在第一组中，证明了FedCorr对数据统计数据和标签质量的差异都是稳健的。
在第二组中，展示了FedCorr的多功能性。当合并FedCorr的前两个阶段时，我们研究了三种最先进的方法的性能改进。

从消融实验中，可以看出不同噪声水平之间的最高精度主要是在低噪声水平下实现的。

Conclusion

这篇提出了FedCorr，一个通用的FL框架，它联合处理本地标签质量和数据统计的差异，并对识别进行了隐私保护的标签校正噪声客户端.

在目前的设计中，FedCorr不考虑动态参与FL，即客户可以在任何时候加入或离开训练。较晚加入的新客户端的用户总是有相对较低的累积LID分数，这意味着新的嘈杂客户可能被错误地归类为干净客户端。因此，还需要做进一步的工作来处理动态参与的问题。