1.为什么要把降维作为一个单独的预处理步骤?
- 复杂度依赖于输入的维度d和数据样本的规模N,为了减少存储量和计算时间。
- 较简单的模型在小数据集上更为鲁棒,较简单的模型具有较小的方差。
- 当数据能够用较少特征解释时,就能够更好地理解解释数据的过程,使得能够提取知识。
- 当数据能够用少数维表示而不丢失信息时,我们可以对数据绘图,并且可视化地分析它的结构和离群点。
降维的主要方法有两个:特征选择和特征提取。特征选择是从原特征中提取特征子集,而特征提取是找出特征的新的组合。最著名的特征提取方法是主成分分析PCA和线性判别分析LDA 。
2.子集选择方法
我们对特征集中的最佳子集感兴趣,它们对正确率的贡献最大。我们丢弃剩余的不重要的维,使用一个合适的误差函数。最佳子集在回归和分类问题中都可以使用。 d d d个变量有 2 d 2^d 2d个可能的子集,但是除非 d d d很小,否则我们不能对所有的子集进行检验。而是采用启发式的方法,在合理的时间内得到一个合理的(但不是最优的)解。
2.1 向前选择
从空集开始,逐个加入特征,每次选择一个降低误差最多的特征,直到进一步的添加不会降低误差(或者降低很少)。
每一步中,我们针对所有可能的
x
i
x_i
xi, 训练模型并在验证集中计算
E
(
F
∪
x
i
)
E(F \cup x_i)
E(F∪xi), (E依赖于应用,误差或者均方误差或者分类错误)。然后选择导致最小误差的输入
x
j
x_j
xj
j
=
a
r
g
m
i
n
i
E
(
F
∪
x
i
)
j=arg min_i E(F \cup x_i)
j=argminiE(F∪xi)
将
x
j
x_j
xj添加到
F
F
F中,如果
E
(
F
∪
x
j
)
<
E
(
F
)
E(F \cup x_j) < E(F)
E(F∪xj)<E(F)。如果当添加任何特征都不会减少E时,停止添加。我们甚至可以提前停止。这里存在一个用户定义的阈值,依赖于应用约束以及错误和复杂度的折中。
这样的过程开销也许会很大,以为将
d
d
d维降到
k
k
k维,我们需要训练和测试系统
d
+
(
d
−
1
)
+
(
d
−
2
)
+
.
.
.
+
(
d
−
k
)
d+(d-1)+(d-2)+...+(d-k)
d+(d−1)+(d−2)+...+(d−k)次,其复杂度为
O
(
d
2
)
O(d^2)
O(d2)。但是这是一个局部搜索过程,并不能保证找到最佳子集,即导致最小误差的最小子集。例如,
x
i
x_i
xi和
x
j
x_j
xj本身可能不好,但是合起来却可能会把误差降低很多。但是该算法是贪婪的,逐个增加特征也许并不能发现
x
i
x_i
xi和
x
j
x_j
xj的并。
以更多计算为代价,可以一次增加m个而不是一个特征。我们还可以在当前添加之后回朔且检查以前添加的哪个特征可以去掉,这增大了搜索空间也增加了复杂度。在浮动搜索方法中,每一步还可以更改增加和去掉的特征数量。
2.2 向后选择
从所有变量开始,逐个排除,每次选择一个去掉它能够使误差最小(或提高误差很少)的变量,直到进一步的排除会显著提高误差。
j
=
a
r
g
m
i
n
i
E
(
F
−
x
i
)
j=arg\ min_i E(F-x_i)
j=arg miniE(F−xi)
从
F
F
F中去掉
x
j
x_j
xj, 如果
E
(
F
−
x
j
)
<
E
(
F
)
E(F-x_j)<E(F)
E(F−xj)<E(F)。
如果去掉特征不能降低误差时我们就停止。为了降低复杂度,可能也会去掉一个它的去掉只会引起很轻微的误差增加的变量。
向前搜索的许多变体对于向后搜索也是可行的。向前与向后方法有着相同的复杂度。但是具体的复杂度取决于系统的特征数目,如果我们预测带有许多无用的特征时,向前搜索更可取。
在这两种方法中,误差检测都应该在不同于训练集上的验证集上进行,因为我们想要检验泛化准确率。使用更多的特征一般会有更低的训练误差,但是不一定有更低的确认误差。这两种方法是监督的,因为误差是根据回归器和分类器计算的。
像是人脸识别这样的应用中,特征选择不是好的方法,因为个体像素本身并不携带很多识别信息。携带脸部识别信息的是许多像素值的组合,这可以通过特征提取方法来实现。
2.3 主成分分析
PCA的思想是将n维特征映射到k维上(k<n),这k为是全新的正交特征。这k维特征称为主成分,是重新构造出来的特征,而不是从原始特征中选择k个特征。
- 求特征协方差矩阵:
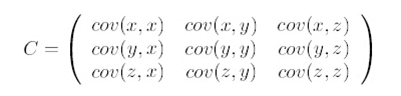
对角线上分别是特征的方差,非对角线上是协方差。协方差是衡量两个变量同时变化的变化程度。协方差大于0代表两个特征正相关,小于0代表负相关。如果x和y统计独立,那么二者的协方差就是0。但是协方差是0,并不能说明x和y是独立的。协方差的绝对值越大,两者对彼此的影响对大。 - 求协方差的特征值和特征向量。将特征值从大到小进行排序,选择其中最大的k个,然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
- 将样本投影到选取的特征向量上。(mn)(nk)=mk 这样原始样本就从n维特征变成了k维,这k维就是原始特征在k维上的投影。
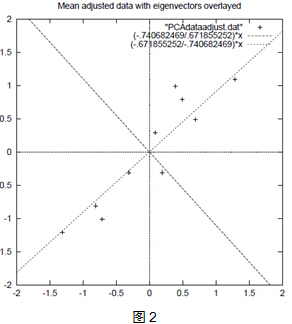
如上图两类样本,斜着的两条线就分别是正交的特征向量(由于协方差矩阵是对称的,所以特征向量正交),最后一步的矩阵乘法就是将原始样本点分别王特征向量对应的轴上做投影。
整个PCA的过程貌似很简单,及时求协方差矩阵的特征值和特征向量,然后做数据转换。但是为什么这个特征向量就是最理想的k维向量?其背后隐藏的意义是什么?整个PCA的意义是什么?
2.3.1 最小二乘法
我们使用最小二乘法来确定各个主轴(主成分)的方向。
对于给定的一组数据
{
z
1
,
z
2
,
.
.
.
,
z
n
}
\{z_1,z_2,...,z_n\}
{z1,z2,...,zn},其数据中心位于
μ
=
1
n
∑
i
=
1
n
z
i
\mu = \frac{1}{n}\sum_{i=1}^{n}z_i
μ=n1∑i=1nzi,将数据中心化(将坐标原点移动到样本点的中心)
{
x
1
,
x
2
,
.
.
.
,
x
n
}
=
{
z
1
−
μ
,
z
2
−
μ
,
.
.
.
,
z
n
−
μ
}
\{x_1,x_2,...,x_n\}=\{z_1-\mu, z_2-\mu, ...,z_n-\mu\}
{x1,x2,...,xn}={z1−μ,z2−μ,...,zn−μ}。
中心化后的数据在第一主轴
μ
1
\mu_1
μ1方向上分散的最开,也就是说在
μ
1
\mu_1
μ1方向上的投影的绝对值之和最大(也可以说方差最大),计算投影的方式就是将x与
μ
1
\mu_1
μ1做内积,由于只需要求
μ
1
\mu_1
μ1的方向,所以设
μ
1
\mu_1
μ1也就是单位向量。
也就是最大化下式:
1
n
∑
i
=
1
n
∣
x
i
⃗
⋅
μ
1
⃗
∣
\frac{1}{n}\sum_{i=1}^{n}|\vec{x_i} \cdot \vec{ \mu_{1}} |
n1i=1∑n∣xi⋅μ1∣
可以对绝对值符号进行平方处理,比较方便,所以进而就是最大化下式:
1
n
∑
i
=
1
n
∣
x
i
⃗
⋅
μ
1
⃗
∣
2
=
1
n
∑
i
=
1
n
(
x
i
⃗
⋅
μ
1
⃗
)
2
\frac{1}{n}\sum_{i=1}^{n}|\vec{x_i} \cdot \vec{ \mu_{1}} |^2=\frac{1}{n}\sum_{i=1}^{n}(\vec{x_i} \cdot \vec{ \mu_{1}} )^2
n1i=1∑n∣xi⋅μ1∣2=n1i=1∑n(xi⋅μ1)2
两个向量做内积,可以转换为矩阵乘法:
x
i
⃗
⋅
μ
1
⃗
=
x
i
T
μ
1
\vec{x_i} \cdot \vec{ \mu_{1}} =x_i^T \mu_{1}
xi⋅μ1=xiTμ1
所以目标函数可以表示为:
1
n
∑
i
=
1
n
(
x
i
T
μ
1
)
2
\frac{1}{n}\sum_{i=1}^{n}(x_i^T \mu_{1} )^2
n1i=1∑n(xiTμ1)2
括号里面就是矩阵乘法表示向量内积,由于列向量转置之后是行向量,行向量乘以列向量得到一个数。而且一个数的转置还是其本身,所以目标函数可以转化为:
1
n
∑
i
=
1
n
(
x
i
T
μ
1
)
T
(
x
i
T
μ
1
)
=
1
n
∑
i
=
1
n
(
μ
1
T
x
i
x
i
T
μ
1
)
=
1
n
μ
1
T
(
∑
i
=
1
n
x
i
x
i
T
)
μ
1
=
1
n
μ
1
T
X
X
T
μ
1
\frac{1}{n}\sum_{i=1}^{n}(x_i^T \mu_{1} )^T(x_i^T \mu_{1}) \\ =\frac{1}{n}\sum_{i=1}^{n}(\mu_{1}^T x_i x_i^T \mu_{1}) \\ = \frac{1}{n}\mu_{1}^T(\sum_{i=1}^{n}x_i x_i^T)\mu_{1} \\= \frac{1}{n}\mu_{1}^TXX^{T}\mu_{1}
n1i=1∑n(xiTμ1)T(xiTμ1)=n1i=1∑n(μ1TxixiTμ1)=n1μ1T(i=1∑nxixiT)μ1=n1μ1TXXTμ1
这就是最终的目标函数,其中
μ
1
T
X
X
T
μ
1
\mu_{1}^TXX^{T}\mu_{1}
μ1TXXTμ1就是一个二次型,我们假设
X
X
T
XX^T
XXT的某一特征值为
λ
\lambda
λ,其对应的特征向量为
ξ
\xi
ξ
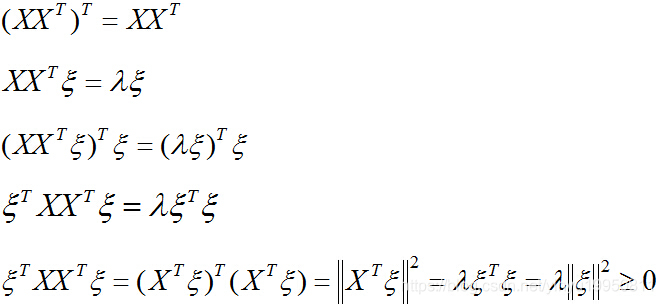
所以特征值
λ
≥
0
\lambda \ge 0
λ≥0,
X
X
T
XX^T
XXT是半正定的对称矩阵,即
μ
1
T
X
X
T
μ
1
\mu_{1}^TXX^{T}\mu_{1}
μ1TXXTμ1是半正定的二次型,所以目标函数存在最大值。
一. 求解最大值
目标函数也可以表示成映射后的向量的二范数平方:
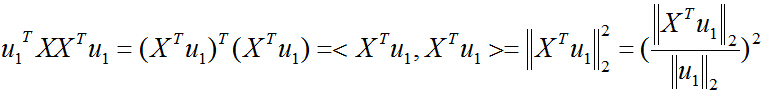
把二次型转化为一个范数的形式,由于
μ
1
\mu_1
μ1取单位向量的形式
,最大化目标函数的基本问题就转化为了:
对于一个矩阵,它对一个向量做变换,变换前后的向量的模长伸缩尺度如何才能最大?我们由矩阵代数中的定理知:向量经矩阵映射前后的向量长度之比的最大值就是这个矩阵的最大奇异值,即: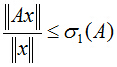
σ
1
\sigma_1
σ1是矩阵A的最大奇异值(亦是矩阵的A的二范数),它等于
A
A
T
AA^T
AAT的最大特征值开平方。针对本问题来说,
X
X
T
XX^T
XXT是半正定对称阵,也就意味着它的特征值都大于等于0,且不同特征值对应的特征向量是正交的,构成所在空间的一组单位正交基。
设对称阵
A
T
A
∈
C
n
∗
n
A^TA \in C^{n*n}
ATA∈Cn∗n的n个特征值为:
λ
1
≥
λ
2
≥
.
.
.
≥
λ
n
≥
0
\lambda_1 \ge \lambda_2 \ge...\ge \lambda_n \ge 0
λ1≥λ2≥...≥λn≥0
相应的单位特征向量为:
ξ
1
,
ξ
2
,
.
.
.
,
ξ
n
\xi_1,\xi_2,...,\xi_n
ξ1,ξ2,...,ξn
任取一个向量x,用特征向量构成的空间中的这组基表示为:
x
=
∑
i
=
1
n
α
i
ξ
i
x=\sum^{n}_{i=1}\alpha_i \xi_i
x=∑i=1nαiξi
则: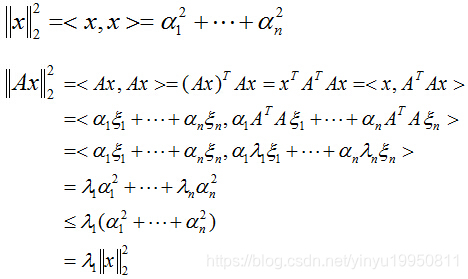
所以:
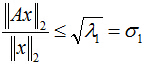
二. 取得最大值时
μ
1
\mu_1
μ1的方向
另
x
=
μ
1
x=\mu_1
x=μ1和
A
=
X
T
A=X^T
A=XT,目标函数
μ
1
X
X
T
μ
1
\mu_1XX^T\mu_1
μ1XXTμ1取得最大值,也就是
m
a
x
(
μ
1
X
X
T
μ
1
)
max(\mu_1XX^T\mu_1)
max(μ1XXTμ1)=
X
X
T
XX^T
XXT的最大特征值。对应的特征向量
μ
1
\mu_1
μ1的方向,就是第一主成分
μ
1
\mu_1
μ1的方向。(第二主成分方向为
X
X
T
XX^T
XXT的第二大特征值对应的特征向量的方向)。
证明完毕。
主成分所占整个信息的百分比:
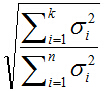
式子中分母为
X
X
T
XX^T
XXT的所有奇异值的平方和,分子为所选取的前k个奇异值平方和。
2.4 线性判别分析
2.4.1两类问题
线性判别分析(Linear discriminant analysis, LDA)是一种用于分类问题的维度归约的监督的方法。我们由两类来开始这个问题的讨论,然后推广到N类中。
给定两个类
C
1
C_1
C1和
C
2
C_2
C2的样本,我们希望找到由向量
w
w
w定义的方向,使得当数据投影到
w
w
w上时,来自两个类的样本尽可能的分开:
z
=
w
T
x
z=w^Tx
z=wTx
z
z
z是
x
x
x到
w
w
w上的投影,因而也是一个从
d
d
d维到1维的维度归约。
m
1
∈
R
d
\bf m_1\in \mathcal{R}^d
m1∈Rd和
m
1
∈
R
m_1 \in \mathcal{R}
m1∈R分别是
C
1
C_1
C1类样本在投影前和投影后的均值。我们有样本
X
=
{
x
t
,
r
t
}
\mathcal{X}=\{x^t, r^t\}
X={xt,rt}, 使得如果
x
t
∈
C
1
x^t \in C_1
xt∈C1,则
r
t
=
1
r^t=1
rt=1,而如果
x
t
∈
C
2
x^t \in C_2
xt∈C2,则
r
t
=
0
r^t=0
rt=0.
m
1
=
∑
t
w
T
x
t
r
t
∑
t
r
t
=
w
T
m
1
m_1=\frac{\sum_t{w}^Tx^tr^t}{\sum_t r^t} = {w}^T{\bf m}_1
m1=∑trt∑twTxtrt=wTm1
m
2
=
∑
t
w
T
x
t
(
1
−
r
t
)
∑
t
(
1
−
r
t
)
=
w
T
m
2
m_2=\frac{\sum_t{w}^Tx^t(1-r^t)}{\sum_t (1-r^t)} = {w}^T{\bf m}_2
m2=∑t(1−rt)∑twTxt(1−rt)=wTm2
来自
C
1
C_1
C1和
C
2
C_2
C2的样本投影后的散布是:
s
1
2
=
∑
t
(
w
T
x
t
−
m
1
)
2
r
t
s_1^2=\sum_t({\bf w}^Tx^t-m_1)^2r^t
s12=t∑(wTxt−m1)2rt
s
2
2
=
∑
t
(
w
T
x
t
−
m
2
)
2
(
1
−
r
t
)
s_2^2=\sum_t({\bf w}^Tx^t-m_2)^2(1-r^t)
s22=t∑(wTxt−m2)2(1−rt)
投影后我们希望均值尽可能的远离,并且类实例散布在尽可能小的区域中。因此,我们希望
∣
m
1
−
m
2
∣
|m_1-m_2|
∣m1−m2∣大,而
s
1
2
+
s
2
2
s_1^2+s_2^2
s12+s22小。
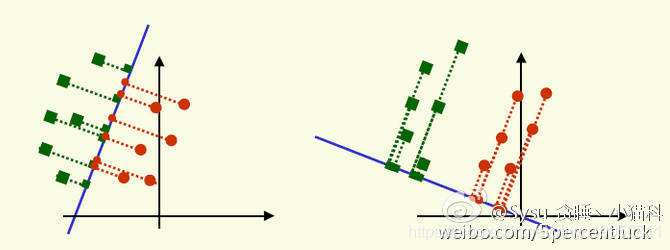
费希尔线性判别式:
J
(
w
)
=
(
m
1
−
m
2
)
2
s
1
2
+
s
2
2
J(w)= \frac{(m_1-m_2)^2}{s_1^2+s_2^2}
J(w)=s12+s22(m1−m2)2
重写分子:
(
m
1
−
m
2
)
2
=
(
w
T
m
1
−
w
T
m
2
)
2
=
w
T
(
m
1
−
m
2
)
(
m
1
−
m
2
)
T
w
=
w
T
S
B
w
(m_1-m_2)^2=(w^T {\bf m_1}-w^T{\bf m_2})^2 \\ =w^T({\bf m_1-\bf m_2})({\bf m_1-\bf m_2})^Tw \\ =w^TS_Bw
(m1−m2)2=(wTm1−wTm2)2=wT(m1−m2)(m1−m2)Tw=wTSBw
其中
S
B
S_B
SB是类间散布矩阵。
分母是投影后类实例在其均值周围散布的和,并且可以改写为:
s
1
2
=
∑
t
(
w
T
x
t
−
m
1
)
2
r
t
=
∑
t
w
T
(
x
t
−
m
1
)
(
x
t
−
m
1
)
T
w
r
t
=
w
T
S
1
w
s_1^2=\sum_t (w^Tx^t-m_1)^2r^t \\ =\sum_tw^T(x^t-{\bf m_1})(x^t-{\bf m_1})^Twr^t \\ =w^TS_1w
s12=t∑(wTxt−m1)2rt=t∑wT(xt−m1)(xt−m1)Twrt=wTS1w
其中
S
1
=
∑
t
r
t
(
x
t
−
m
1
)
(
x
t
−
m
1
)
T
S_1=\sum_tr^t(x^t-m_1)(x^t-m_1)^T
S1=∑trt(xt−m1)(xt−m1)T是
C
1
C_1
C1的类内散布矩阵。
S
1
/
∑
t
r
t
S_1/\sum_tr^t
S1/∑trt是
∑
1
\sum_1
∑1的估计。
并且我们得到
s
1
2
+
s
2
2
=
w
T
S
w
w
s_1^2+s_2^2 = w^TS_ww
s12+s22=wTSww
其中
S
w
=
S
1
+
S
2
S_w=S_1+S_2
Sw=S1+S2是类内散布的总和。(
s
1
2
+
s
2
2
s_1^2+s_2^2
s12+s22)除以样本总数是汇聚数据的方差。
J
(
w
)
J(w)
J(w)可以改写为:
J
(
w
)
=
w
T
S
B
w
w
T
S
W
w
=
∣
w
T
(
m
1
−
m
2
)
∣
2
w
T
S
W
w
J(w) = \frac{w^TS_Bw}{w^TS_Ww}=\frac{|w^T(m_1-m_2)|^2}{w^TS_Ww}
J(w)=wTSWwwTSBw=wTSWw∣wT(m1−m2)∣2
关于
w
w
w取
J
J
J的导数并令其等于0,我们得到:
w
=
c
S
W
−
1
(
m
1
−
m
2
)
w=cS_W^{-1}({\bf m_1}- {\bf m_2})
w=cSW−1(m1−m2)
其中c是某个常数,因为对我们来说重要的是方向,而不是大小,所以我们可以取
c
=
1
c=1
c=1并且找出
w
w
w。
记住当
p
(
x
∣
C
i
)
p(x|C_i)
p(x∣Ci)~
N
(
μ
i
,
∑
)
\mathcal{N}(\mu_i, \sum)
N(μi,∑)时, 有线性判别式,其中
w
=
∑
−
1
(
μ
1
−
μ
2
)
w=\sum^{-1}(\mu_1-\mu_2)
w=∑−1(μ1−μ2).并且如果类是正态分布的,则费希尔线性判别式是最优的。在同样的假设下,我们还可以计算
w
0
w_0
w0来分开两个类。但是,其在类不是正态分布时也能够使用。已经把样本从
d
d
d维降到
1
1
1维,之后可以使用任何分类方法。
2.4.2 多类情况
在K>2的情况下,希望找到这样的矩阵W,使得:
x
=
W
T
x
x=W^Tx
x=WTx
其中
z
z
z是
k
k
k维的,
W
W
W是
d
∗
k
d*k
d∗k矩阵。
总类内散布矩阵是:
S
W
=
∑
i
=
1
K
S
i
S_W=\sum_{i=1}^KS_i
SW=i=1∑KSi
其中
S
i
S_i
Si是
C
i
C_i
Ci的类内散布矩阵:
S
i
=
∑
t
r
i
t
(
x
t
−
m
i
)
(
x
t
−
m
i
)
T
S_i=\sum_tr_i^t(x^t-{\bf m}_i)(x^t-{\bf m}_i)^T
Si=∑trit(xt−mi)(xt−mi)T(if
x
t
∈
C
i
x^t \in C_i
xt∈Ci, then
r
i
t
=
1
r_i^t=1
rit=1).
类间散布矩阵: 当存在K>2个类时,每个类均值的散布根据它们在总均值周围的散布情况计算:
m
=
1
K
∑
i
=
1
K
m
i
{\bf m} = \frac{1}{K}\sum^K_{i=1}{\bf m}_i
m=K1i=1∑Kmi
而类间散布矩阵是:
S
B
=
∑
i
=
1
K
N
i
(
m
i
−
m
)
(
m
i
−
m
)
T
S_B=\sum^K_{i=1}N_i({\bf m_i}- {\bf m})({\bf m_i}- {\bf m})^T
SB=i=1∑KNi(mi−m)(mi−m)T
其中
N
i
=
∑
t
r
i
t
N_i=\sum_tr^t_i
Ni=∑trit, 投影后的类内散布矩阵和类间散布矩阵是
W
T
S
B
W
W^TS_BW
WTSBW和
W
T
S
W
W
W^TS_WW
WTSWW,它们都是
k
∗
k
k*k
k∗k的矩阵。我们希望类间散布矩阵大,也就是说在投影之后,在新的
k
k
k维空间,我们希望类均值之间互相尽可能的远离。希望类内散布矩阵小,也就是希望投影之后来自同一类别的样本尽可能的接近他们的均值。
对于一个散布(协方差)矩阵来说,散布的一个度量是行列式。该行列式是特征值的乘积,而特征值给出沿着它的特征向量的方差。因此,我们对最小化J(w)的矩阵W感兴趣:
J
(
W
)
=
∣
W
T
S
B
W
∣
∣
W
T
S
W
W
∣
J(W)=\frac{|W^TS_BW|}{|W^TS_WW|}
J(W)=∣WTSWW∣∣WTSBW∣
S
W
−
1
S
B
S_W^{-1}S_B
SW−1SB的最大特征向量是解。
S
B
S_B
SB是K个秩为1的矩阵
(
m
i
−
m
)
(
m
i
−
m
)
T
({\bf m_i}- {\bf m})({\bf m_i}- {\bf m})^T
(mi−m)(mi−m)T的和, 并且它们之中只有
K
−
1
K-1
K−1个是独立的。因此,
S
B
S_B
SB具有最大秩
K
−
1
K-1
K−1。这样我们定义一个新的较低的K-1维空间,然后在那里构造判别式。虽然LDA使用类分离性作为它的好坏标准,但是在这个新空间中可以使用任意的分类方法来估计判别式。
对于分类来说,与向前和向后方法对比来说,取代每步训练一个分类器并对它进行测试,线性判别式中采用启发式的方法,来度量新空间把类彼此分开的质量。 我们讨论的投影方法是批过程,因为它们要求在发现投影方向之前给定整个的样本,而且该线性投影方法具有局限性,在许多应用中,特征以非线性方式互相影响,需要非线性特征提取方法。
总结
特征提取与决策制定之间有一个权衡。如果特征提取的好,分类和回归的任务变得微不足道。另一方面,如果分类做的足够好,则没有必要进行特征选取,它会自动的特征选择或者内部组合(决策树在产生决策树时进行特征选择,而多层感知机在隐藏结点做非线性的特征提取),我们处于这两个理想世界之间。我们期望在耦合特征提取和其后的分类或回归方法取得更多进展。
参考:
1.机器学习导论
2PCA























 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








