原文参考
https://onlinecourses.science.psu.edu/stat857/node/11
http://www.doc88.com/p-315762247283.html
http://wenku.baidu.com/link?url=OrBkfJFwZ_l8soN6CRE2B1KAI-988Z0wrzG_K59W39l7ycRTNd6xeH6hFUnRugEywPz1TUsvclcjpeiS8JLJsnd97GrQdHeG4r70BtSTIsS
https://www.cs.nyu.edu/~roweis/papers/llejmlr.pdf
http://arxiv.org/pdf/cs/0212008v1.pdf
多元统计分析
等…
本章主要学习目标:
在第4章中,我们了解了压缩变量的算法,接下来我们熟悉一下高维数据的降维方法。
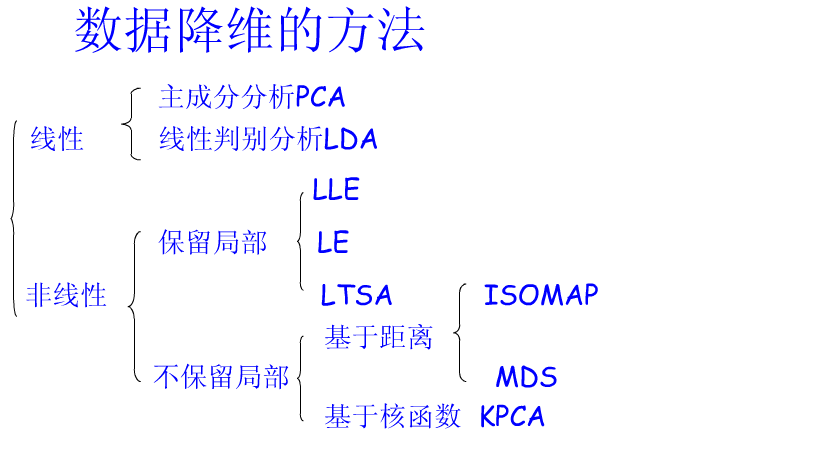
传统的降维方法包括PCA、LDA,流行学习算包括LLE、ISOMAP、LE、LTSA,如下图:
1, 主成分分析PCA
首先我们定义,输入矩阵X是n*p维的。行代表样本,列代表变量。且X是中心化的,每一列去掉均值。
1.1 奇异值分解(SVD)
由现行代数的定理可知,如果一个矩阵A是对称矩阵,那么其一定可以正交对角化。即,存在一个正交矩阵P和一个对角矩阵D使得
A
=
P
D
P
−
1
=
P
D
P
T
A=PDP^{-1}=PDP^T
A=PDP−1=PDPT
那么,A不是对称矩阵的时候呢?
这时就引出了奇异值分解,且任何矩阵都能进行奇异值分解。
假设A是m*n维矩阵,那么
A
T
A
A^TA
ATA一定是对称的,可正交对角化。假设v是
A
T
A
A^TA
ATA的单位正交基构成的特征向量、λ是对应的特征值,则有:
A
T
A
v
=
λ
v
A^TAv=λv
ATAv=λv
∣
∣
A
v
∣
∣
2
=
v
T
A
T
A
v
=
v
T
λ
v
=
λ
(
v
是
由
单
位
正
交
基
构
成
的
)
||Av||^2=v^TA^TAv=v^Tλv=λ(v是由单位正交基构成的)
∣∣Av∣∣2=vTATAv=vTλv=λ(v是由单位正交基构成的)
∣
∣
A
v
∣
∣
=
∣
∣
A
v
∣
∣
2
=
λ
=
σ
||Av||=\sqrt{||Av||^2}=\sqrt{λ}=σ
∣∣Av∣∣=∣∣Av∣∣2=λ=σ
定义
σ
=
λ
σ=\sqrt{λ}
σ=λ为矩阵A的奇异值,且奇异值是向量Av的长度。
我们令向量
u
=
A
v
∣
∣
A
v
∣
∣
=
A
v
σ
u=\frac{Av}{||Av||}=\frac{Av}{σ}
u=∣∣Av∣∣Av=σAv
则我们得到,Av=σu
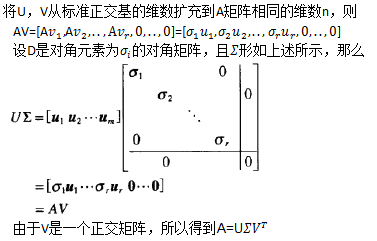
同理,对于n×p 输入矩阵X,可以分解为 X = U D V T X=UDV^T X=UDVT
1.2 主成分
主成分分析是线性降维的主要方法:
样本X的协方差矩阵,为
S
=
X
T
X
/
N
S=X^TX/N
S=XTX/N
(注明:因为X已经进行了中心化的处理,所以协方差矩阵可以如上式表示)
如果对
X
T
X
X^TX
XTX进行奇异值变换,得
X
T
X
=
V
D
U
T
U
D
V
T
=
V
D
2
V
T
X^TX=VDU^TUDV^T=VD^2V^T
XTX=VDUTUDVT=VD2VT
向量v称为X的(principal component directions)主成分方向坐标基(v已经单位化),如果将X投影到该坐标基上面,就得到了对应的主成分分量。
综上,我们容易得出
z
j
=
X
j
∗
v
j
=
u
j
∗
d
j
z_j=X_j*v_j=u_j*d_j
zj=Xj∗vj=uj∗dj
u
j
u_j
uj是
x
j
x_j
xj的行向量沿着
v
j
v_j
vj向量方向上投影得到的,投影的尺度通过
d
j
d_j
dj来控制.
所以,
- X的主成分为 z j = u j ∗ d j , j = 1 , . . . , p z_j=u_j*d_j,j=1,...,p zj=uj∗dj,j=1,...,p
- 主成分应该是按照其方差由大到小排序的,根据下面公式可知,按照奇异值的大小排序即得可得到我们想要的排序.
v a r ( z ) = 1 N ∗ ( z − 0 ) 2 var(z)=\frac{1}{N}*(z-0)^2 var(z)=N1∗(z−0)2
v a r ( z ) = 1 N ( u ∗ d ) 2 = 1 N d T u T u d = d 2 N var(z)=\frac{1}{N}(u*d)^2=\frac{1}{N}d^Tu^Tud=\frac{d^2}{N} var(z)=N1(u∗d)2=N1dTuTud=Nd2
(因为已经中心化,所以均值为零)
1.3 主成分回归-principal components regression (PCR).
前面我们讲的PCA,是一种无监督学习方法,而PCR就是主成分与线性回归的结合,假设提取了M个主成分 z 1 , . . . , z m z_1,...,z_m z1,...,zm,然后求
y = β 1 z 1 + . . . + . . . + β m z m y=β_1z_1+...+...+β_mz_m y=β1z1+...+...+βmzm
有时候,PCR的效果并不一定比第6章讲的方法要好,只不过PCA是一个很好的降维方法,在PCA的基础上衍生出来的PCR也是对高维样进行回归的一个重要的参考方向。
1.4 偏最小二乘回归-partial least squares (PLS).
偏最小二乘回归结合了多元线性回归、主成分分析以及典型相关分析。
偏最小二乘回归与主成分回归的不同之处在于,主成分回归产生的权重矩阵反映的是预测变量X之间的协方差,而偏最小二乘回归产生的权重矩阵反映的是预测变量X与响应变量Y之间的协方差。
之所以分解矩阵变为X与Y的协方差矩阵,是因为,主成分分析中,会忽略掉那些可能对Y起决定性作用的、但是与其他变量相关性又很小的变量。且主成分只能很好的解释了X,但是并不能保证一定与Y有关。相对的,PLS中分解得到的成分(潜变量),是抽取了与Y相关的X的主要信息。这点上,使得PLS可能比PCR得到更准确的回归。
(1) 典型相关分析
典型相关分析(Canonical Correlation Analysis),是考察一组X变量和一组Y变量(两个及以上Y变量)之间的线性关系的方法。
1936年,Hotelling提出典型相关分析。考虑两组变量的线性组合, 并研究它们之间的相关系数p(T,U).在所有的线性组合中, 找一对相关系数最大的线性组合, 用这个组合的单相关系数来表示两组变量的相关性, 叫做两组变量的典型相关系数, 而这两个线性组合叫做一对典型变量。在两组多变量的情形下, 需要用若干对典型变量才能完全反映出它们之间的相关性。下一步, 再在两组变量的与t1,u1不相关的线性组合中, 找一对相关系数最大的线性组合, 它就是第二对典型变量, 而且p(t2,u2)就是第二个典型相关系数。这样下去, 可以得到若干对典型变量, 从而提取出两组变量间的全部信息。
令,典型变量可被表示为如下形式:
t
=
a
1
x
1
+
.
.
.
+
a
m
x
m
;
t=a_1x_1+...+a_mx_m;
t=a1x1+...+amxm;
u
=
b
1
x
1
+
.
.
.
+
b
n
x
n
;
u=b_1x_1+...+b_nx_n;
u=b1x1+...+bnxn;
然后,我们可以求解t,u的相关系数: Cor(t,u)
最后,用线性规划的方法求解使得Cor(t,u)最大的参数a和b。
(2) 典型相关的思想下,如何求解PLS:
假设要对,因变量
Y
=
Y
1
,
.
.
.
,
Y
p
Y=Y_1,...,Y_p
Y=Y1,...,Yp,
自变量
X
=
X
1
,
.
.
.
,
X
m
X=X_1,...,X_m
X=X1,...,Xm,的样本对象进行建模。
PLS的做法是:
首先,在自变量集中提取第一成分
T
1
T_1
T1
T
1
=
w
11
X
1
+
.
.
.
+
w
1
m
X
m
T_1=w_{11}X_1+...+w_{1m}X_m
T1=w11X1+...+w1mXm
同时,也在因变量集中提取第一成分
U
1
U_1
U1
U
1
=
v
11
Y
1
+
.
.
.
+
v
1
p
Y
p
U_1=v_{11}Y_1+...+v_{1p}Y_p
U1=v11Y1+...+v1pYp
求解目标,为
m
a
x
(
T
1
)
−
>
m
a
x
max(T_1)->max
max(T1)−>max
m
a
x
(
U
1
)
−
>
m
a
x
max(U_1)->max
max(U1)−>max
C
o
r
r
(
T
1
,
U
1
)
−
>
m
a
x
Corr(T1,U1)->max
Corr(T1,U1)−>max
且,
∣
∣
w
1
∣
∣
=
∣
∣
v
1
∣
∣
=
1
||w_1||=||v_1||=1
∣∣w1∣∣=∣∣v1∣∣=1
然后,建立 Y Y Y与 T 1 T_1 T1的,以及 X X X与 T 1 T_1 T1的回归方程。如果回归方程的精度达到满意程度,则终止算法;否则继续提取第二成分…(假设直到 T r T_r Tr为止)。
X
0
=
t
1
α
1
′
+
E
1
X_0=t_1α_1' + E_1
X0=t1α1′+E1
Y
0
=
t
1
β
1
′
+
F
1
Y_0=t_1β_1' + F_1
Y0=t1β1′+F1
其中,
t
1
t_1
t1为n维向量,
α
1
′
=
(
α
11
,
.
.
.
,
α
1
m
)
,
β
1
′
=
(
β
11
,
.
.
.
,
β
1
p
)
α_1'=(α_{11},...,α_{1m}), β_1'=(β_{11},...,β_{1p})
α1′=(α11,...,α1m),β1′=(β11,...,β1p)
E
1
和
F
1
分
别
是
残
差
矩
阵
E_1和F_1分别是残差矩阵
E1和F1分别是残差矩阵
如果精度没有满足,则继续用回归得到残差矩阵
E
1
,
F
1
E_1,F_1
E1,F1继续回归,得到
t
2
,
α
1
′
.
.
.
t_2,α_1'...
t2,α1′...
最后,PLS通过建立Y与 T 1 , . . . , T r T_1,...,T_r T1,...,Tr的回归方程,进而表示为Y与原自变量X的回归方程,实现偏最小二乘回归方程。
关于PLS的R实现,可以阅读此书。
2 线性判别分析LDA
LDA的全称是Linear Discriminant Analysis(线性判别分析),是一种supervised learning。有些资料上也称为是Fisher’s Linear Discriminant,因为Ronald Fisher在1936年发明了这个算。
LDA的原理是将带有类标签的数据投影到低维空间,投影后,使得统一类标签的样本数据"更近",不同类之间"更远"。LDA算法涉及到了降维的思想,而且其本身也是一种分类方法。
具体实现步骤如下:
- 样本的类别数为c,下面以c=2为例;
- w是n维空间中任一向量,x在w上的投影为 w T x w^Tx wTx
-
m
i
m_i
mi为所属c类的x的样本的质心,令
m 1 = 1 N 1 ∑ n ∈ c 1 w T x n m_1=\frac{1}{N_1}\sum_{n∈c_1}{w^Tx_n} m1=N11∑n∈c1wTxn;
m 2 = 1 N 2 ∑ n ∈ c 2 w T x n m_2=\frac{1}{N_2}\sum_{n∈c_2}{w^Tx_n} m2=N21∑n∈c2wTxn; - Fisher 判别准则,为
J ( w ) = ( m 2 − m 1 ) 2 s 1 2 + s 2 2 J(w)=\frac{(m_2-m_1)^2}{s_1^2+s_2^2} J(w)=s12+s22(m2−m1)2
等价于:
J ( w ) = w t S B w w t S w w J(w)=\frac{w^tS_Bw}{w^tS_ww} J(w)=wtSwwwtSBw
其中,
S B = ( m 2 − m 1 ) ( m 2 − m 1 ) T S_B=(m_2-m_1)(m_2-m_1)^T SB=(m2−m1)(m2−m1)T
表示类间离散度矩阵
S W S_W SW
表示类内离散度矩阵
5,求解W
W是我们要求得的投影向量。我们通过W生成新的坐标轴,使不同类别的样本数据在新Y轴的投影中能最大程度的分离。
$max: $
J
(
w
)
=
w
t
S
B
w
w
t
S
w
w
J(w)=\frac{w^tS_Bw}{w^tS_ww}
J(w)=wtSwwwtSBw
$s.t. $
W
t
W
=
I
W^tW=I
WtW=I
在人脸识别中,Belhumeur等人用PCA将人脸图像投影到一个子空间,然后再实施LDA,得到最终的投影矩阵 U = U p c a U l d a U=U_{pca}U_{lda} U=UpcaUlda 命名为"Fisherfaces"
此外,基于LDA,还有许多衍生的判别模型:
Mixture Discriminant Analysis (MDA)
Gaussian Discriminant Analysis(GDA)
Quadratic Discriminant Analysis (QDA)
Flexible Discriminant Analysis (FDA)
3 局部线性嵌入LLE
简单的讲,该方法是把高维空间数据点按维数映射到低维嵌入空间,即Xi→Yi。
整个问题最后被转化为两个二次规划问题。
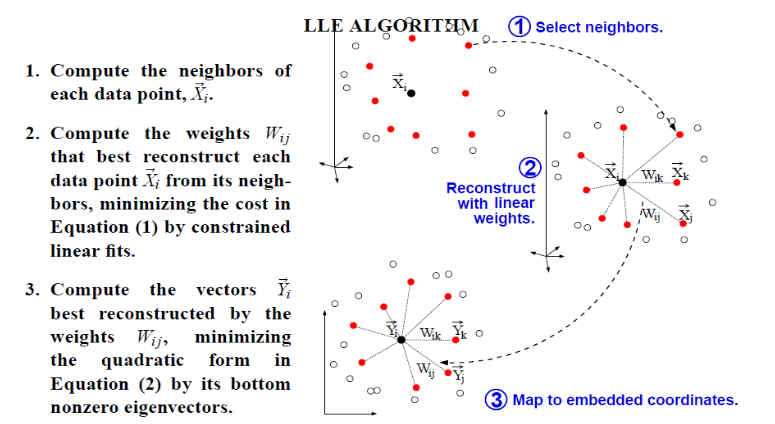
LLE(ocal linear embedding)算法可以归结为三步:
- 寻找每个样本点 X i X_i Xi的k个近邻点;
- 由每个样本点 X i X_i Xi的近邻点计算出该样本点的局部重建权值矩阵 W i j W_{ij} Wij;
- 由该样本点的局部重建权值矩阵
W
i
j
W_{ij}
Wij和其近邻点计算出对应的低维向量
Y
i
Y_i
Yi.
E
(
W
)
=
∑
i
∣
X
i
−
∑
j
W
i
j
X
j
∣
2
E(W)=\sum_i{| X_i - \sum_j{W_{ij}X_j} |}^2
E(W)=∑i∣Xi−∑jWijXj∣2 - - - - - - - -Equation(1)
其中,
X
j
X_j
Xj表示
X
i
X_i
Xi点的第j个近邻,且对于非近邻点
W
i
j
=
0
W_ij=0
Wij=0,对于近邻点
∑
j
W
i
j
=
1
\sum_j{W_{ij}}=1
∑jWij=1
在限制条件下,通过上述方程1,最小化重构错误E(W)得到的最优权值W,遵循如下对称特性,即对于特定的数据点,在其本身和其邻居数据点有旋转、缩放、平移操作时将保持其原有性质不变。
f
(
Y
)
=
∑
i
∣
Y
i
−
∑
j
W
i
j
Y
j
∣
2
f(Y)=\sum_i{| Y_i - \sum_j{W_{ij}Y_j} |}^2
f(Y)=∑i∣Yi−∑jWijYj∣2 - - - - - - - -Equation(2)
其中,
Y
i
Y_i
Yi是输出向量,
Y
j
Y_j
Yj表示
Y
i
Y_i
Yi的第j个近邻,
且满足
∑
y
i
=
0
\sum{y_i}=0
∑yi=0;
1
N
∑
y
i
y
i
′
=
I
\frac{1}{N}\sum{y_iy_i'}=I
N1∑yiyi′=I
根据方程1得到权重W后,根据上述方程2,求解得到输出向量Y。将所有的样本点映射到低维空间,即在低维空间中,根据W的几何信息进行点的重建。
根据方程2的满足条件,求解:min(f(x))
在整个求解过程中,近邻K的个数是很重要的,但是其仅仅是个经验参数,并没有很好的办法进行确定,通常算法规定K必须大于样本输出的维数。
选取最优的K
应满足,在选取K条件下,应用LLE算法,使得输入点的相对位置与输出点的相对位置尽量保持一致。通常映射的好坏,可以通过输入点与输出点之间的偶合情况来表示。(输入点之间的距离矩阵和输出点之间的距离矩阵的关系系数衡量)
k o p t = a r g m i n ( 1 − ρ D x , D y ) 2 k_{opt}=argmin(1-ρ_{D_x,D_y})^2 kopt=argmin(1−ρDx,Dy)2
其中,ρ表示两个矩阵间的标准线性相关系数。
D
x
D_x
Dx表示输入样本(高维)之间的距离矩阵,
D
y
D_y
Dy表示输出样本(低维)之间的距离矩阵。
4 拉普拉斯特征映射LE
Laplacian Eigenmaps与LLE方法有一些共有的特性。都是对几何流行(manifold)进行降维方法。
拉普拉斯矩阵的一些特性已经被广泛用于聚类(如谱聚类)和划分问题。某种意义上讲,聚类和降维是一个问题的正反面,所以LE算法试图通过拉普拉斯矩阵的相关方法把问题从谱聚类中转向降维。
假设:
在
R
l
R^l
Rl空间中,有
x
1
,
.
.
.
,
x
k
x_1,...,x_k
x1,...,xk,k个点
我们的目标是
在
R
m
R^m
Rm(m远远小于l)空间中,找到
y
1
,
.
.
.
,
y
k
y_1,...,y_k
y1,...,yk
使得在低维空间中的
y
i
y_i
yi可以"代表"高维空间中的
x
i
x_i
xi
LE算法:
1). 构建邻接图( Adjacency Graph)
计算两个近邻点
x
i
,
x
j
x_i,x_j
xi,xj之间的距离,如果认为两个点是“相近”的,则在两点之间添加一条边。如何判断"相近",有两种方法:
a). 根据阈值ε来判断
∣
∣
x
i
−
x
j
∣
∣
2
<
ε
||x_i-x_j||^2<ε
∣∣xi−xj∣∣2<ε
凡是满足上述等式的就算作近邻
缺点:很难确定ε;优点:保留了几何上的对称性
b). 根据个数n来判断
通过计算n个最近的点作为近邻
缺点:非几何特性驱动,可能很远的第n个点也作为近邻
优点:很容易选择,不会出现断开的图
2). 计算边的权重
计算边的权重来描述两个点之间的“远近”程度,同样有两种方法来计算边的权重:
a). 利用热核函数,如果点i和点j是连接的(确定是近邻点),则
W
i
j
=
e
−
∣
∣
x
i
−
x
j
∣
∣
2
t
W_{ij}=e^{-\frac{||x_i-x_j||^2}{t}}
Wij=e−t∣∣xi−xj∣∣2
如果不是近邻,则,
W
i
j
=
0
W_{ij}=0
Wij=0
b). 简单模式:t->∞ , 即有连接的时候 W i j = 1 W_{ij}=1 Wij=1,否则为0.
3). 特征映射(eigenmaps)
拉普拉斯矩阵的定义:
假定一个图G的邻接矩阵为A,度矩阵为D,则该图的拉普拉斯矩阵L为:
L
=
D
−
A
L=D-A
L=D−A
其中,D为度矩阵,是图中每个点的度(出度入度不重复计算),所以D是对称矩阵,且除了对角线其余位置元素均为零。
结合前两点,此处,我们定义:
D
i
i
=
∑
j
W
j
i
.
D_{ii}=\sum_{j}{W_{ji.}}
Dii=∑jWji.
区别:
当权重的计算用的是热核函数(t≠∞),那么其权值可能为非整数,所以矩阵D中的元素可能是非整数的,这是与常规定义的度矩阵的差异。
所以,LE算法中的拉普拉斯矩阵定义为: L = D − W L=D-W L=D−W
计算其特征值与特征向量:
L
f
=
λ
D
f
Lf=λDf
Lf=λDf
可以得到k个特征向值,并对其进行排序,得到
λ
0
,
.
.
.
,
λ
k
−
1
λ_0,...,λ_{k-1}
λ0,...,λk−1,且
0
=
λ
0
≤
λ
1
,
.
.
.
≤
.
.
.
,
λ
k
−
2
≤
λ
k
−
1
0=λ_0≤λ_1,...≤...,λ_{k-2}≤λ_{k-1}
0=λ0≤λ1,...≤...,λk−2≤λk−1
不考虑0值,我们取较大的特征值λ
x
i
−
>
(
f
1
(
i
)
,
.
.
.
,
f
m
(
i
)
)
x_i->(f_1(i),...,f_m(i))
xi−>(f1(i),...,fm(i))
作为m维欧几里得空间
5 局部切空间排列算法LTSA
LTSA算法的思想是找出每个数据点的邻近点,用邻域中低维切空间的坐标近似表示局部的非线性几何特征;再通过变换矩阵将各数据点邻域切空间的局部坐标映射到统一的全局坐标上;最后,经过一些列数学推导,将求解整体嵌入坐标问题转换为求解矩阵的特征值问题,从而实现高维数据的维度约简。
具体实现步骤如下:
- 选取邻域。
对样本点 x i x_i xi,选取包含其自身在内的k个近邻点作为邻域; x i j ( j = 1 , . . , k ) x_{ij} (j=1,..,k) xij(j=1,..,k)是其k个邻近点; x ˉ i \bar{x}_i xˉi 为上述k个邻近值的均值; - 局部线性拟合。
计算点 x i x_i xi处d维切空间的正交基 Q i Q_i Qi和每一个 x i j x_{ij} xij在切空间上的正交投影 θ j i = Q i T ( x i j − x ˉ i ) θ_j^i=Q_i^T(x_{ij}-\bar{x}_i) θji=QiT(xij−xˉi) - 局部坐标整合
根据n个局部投影 θ i = [ θ 1 i , θ 2 i , . . . , θ k i ] θ^i=[θ_1^i,θ_2^i,...,θ_k^i] θi=[θ1i,θ2i,...,θki],计算全局坐标 T= { τ i } i = 1 n \{\tau_{i}\}^n_{i=1} {τi}i=1n,
τ i = [ τ i 1 , τ i 2 , . . . , τ i k ] \tau_{i}=[\tau_{i1},\tau_{i2},...,\tau_{ik}] τi=[τi1,τi2,...,τik]
6 MDS
MDS是通过对样本数据的相似性矩阵(相关矩阵或距离矩阵)进行适当的谱分解,得到能够近似表示高维数据的相对构造的、在低维空间中的投影,进而对原数据进行降维的一种方法。其思想和主成分分析(PCA)非常相似。在欧氏距离之下,这种算法求得的主坐标(principal coordinates)相当于PCA中前t个主成分的得分。
假设输入矩阵为
X
=
x
1
,
x
2
,
.
.
.
,
x
n
∈
R
p
;
X=x_1,x_2,...,x_n ∈R^p;
X=x1,x2,...,xn∈Rp;
X的距离阵为
D
=
(
d
i
j
)
D=(d_{ij})
D=(dij)
d
i
j
2
=
(
x
i
−
x
j
)
T
(
x
i
−
x
j
)
.
d^2_{ij}=(x_i-x_j)^T(x_i-x_j).
dij2=(xi−xj)T(xi−xj).
算法步骤:
1), 根据距离阵D计算矩阵B
定理: 令
A
=
(
a
i
j
)
,
a
i
j
=
−
1
2
d
i
j
2
A=(a_{ij}),a_{ij}=-\frac{1}{2}d_{ij}^2
A=(aij),aij=−21dij2,
H
=
I
n
−
1
n
1
n
1
n
′
H=I_n-\frac{1}{n}{1_n1_n'}
H=In−n11n1n′ 是中心化的变化矩阵
B
=
H
A
H
B=HAH
B=HAH
则,
D
D
D 是欧式型的距离阵的充要条件:
B
B
B 是半正定矩阵,即
B
≥
0
B≥0
B≥0
必要性证明:
设D是欧式型的,则存在
x
i
x_i
xi,使得两点的距离:
d
i
j
2
=
(
x
i
−
x
j
)
T
(
x
i
−
x
j
)
=
−
2
a
i
j
d_{ij}^2=(x_i-x_j)^T(x_i-x_j)=-2a_{ij}
dij2=(xi−xj)T(xi−xj)=−2aij
由矩阵B的定义,得
B
=
H
A
H
=
A
−
1
n
A
J
−
1
n
J
A
+
1
n
2
J
A
J
B=HAH=A-\frac{1}{n}AJ-\frac{1}{n}JA+\frac{1}{n^2}JAJ
B=HAH=A−n1AJ−n1JA+n21JAJ
,其中
J
=
1
n
1
n
′
J=1_n1_n'
J=1n1n′
可得,
b
i
j
=
(
a
i
j
−
a
‾
i
.
−
a
‾
.
j
+
a
‾
.
.
)
b_{ij}=(a_{ij}-\overline{a}_{i.}-\overline{a}_{.j}+\overline{a}_{..})
bij=(aij−ai.−a.j+a..)
其中,
a
‾
i
.
=
1
n
∑
j
=
1
n
a
i
j
\overline{a}_{i.}=\frac{1}{n}\sum_{j=1}^{n}{a_{ij}}
ai.=n1∑j=1naij
a
‾
.
j
=
1
n
∑
i
=
1
n
a
i
j
\overline{a}_{.j}=\frac{1}{n}\sum_{i=1}^{n}{a_{ij}}
a.j=n1∑i=1naij
a
‾
.
.
=
1
n
2
∑
i
=
1
n
∑
j
=
1
n
a
i
j
\overline{a}_{..}=\frac{1}{n^2}\sum_{i=1}^{n}\sum_{j=1}^{n}{a_{ij}}
a..=n21∑i=1n∑j=1naij
再带入 − 2 a i j = ( x i − x j ) T ( x i − x j ) -2a_{ij}=(x_i-x_j)^T(x_i-x_j) −2aij=(xi−xj)T(xi−xj)
得,
b
i
j
=
(
x
i
−
x
‾
)
T
(
x
i
−
x
‾
)
b_{ij}=(x_i-\overline{x})^T(x_i-\overline{x})
bij=(xi−x)T(xi−x)
可推得
B
=
(
H
X
)
(
H
X
)
T
≥
0
B=(HX)(HX)^T≥0
B=(HX)(HX)T≥0
必要性证毕.
充分性证明:
当B≥0时,记Λ = diag(
λ
1
,
.
.
.
,
λ
k
λ_1, . . . , λ_k
λ1,...,λk)
为B的特征根对角矩阵,
Γ 为对应的n*k 维特征向量矩阵
则,
B
=
Γ
Λ
Γ
T
B=ΓΛΓ_T
B=ΓΛΓT
定义
B
=
Γ
Λ
1
/
2
B=ΓΛ^{1/2}
B=ΓΛ1/2,则
B
=
Z
Z
T
B=ZZ^T
B=ZZT
- 对矩阵B进行谱分解
7 ISOMAP
Isomap以MDS为计算工具,创新之处在于计算高维流形上数据点间距离时,不是用传统的欧式距离,而是采用微分几何中的测地线距离(或称为曲线距离),并且找到了一种用实际输入数据估计其测地线距离的算法(即图论中的最小路径逼近测地线距离)。
8 KPCA
入svm一样,KPCA运用了核方法对技巧,将原空间中的数据映射到高维空间.
K
(
x
i
,
x
j
)
=
φ
(
x
i
)
T
φ
(
x
j
)
K(x_i,x_j)=φ(x_i)^Tφ(x_j)
K(xi,xj)=φ(xi)Tφ(xj)
利用核技巧,我们可以非线性空间
φ
(
x
i
)
φ(x_i)
φ(xi)使用pca方法








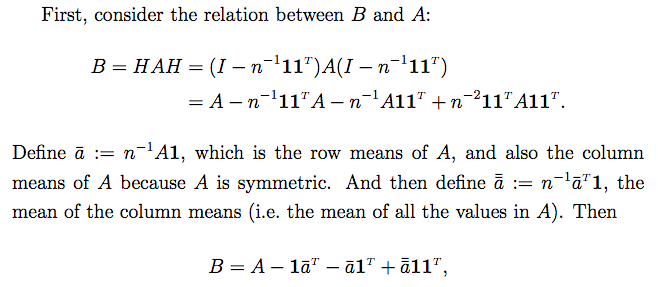

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








