Simplex Noise （三）

一、3D Simplex Noise

  在学习完２D Simplex 噪声之后，３D Simplex噪声实现就很简单了，按照之前学习的，我们还是按照分步的方法来实现3D Simplex 噪声。

（一）、坐标变换（Coordinate skewing）。

  根据变换公式，我们可以很容易的实现顶点在单形与其对应的正超晶格之间进行变换，不再赘述，代码如下：

            double F3 = 1.0 / 3.0;
            int I0 = GetFloor(x + (x + y + z) * F3);
            int J0 = GetFloor(y + (x + y + z) * F3);
            int K0 = GetFloor(z + (x + y + z) * F3);

            double G3 = 1.0 / 6.0;
            double i0 = I0 - (I0 + J0 + K0) * G3; ;
            double j0 = J0 - (I0 + J0 + K0) * G3; ;
            double k0 = K0 - (I0 + J0 + K0) * G3; ;
            double dx0 = x - i0;
            double dy0 = y - j0;
            double dz0 = z - k0;

  在上面的代码中，我们还得到输入点到第一个单形顶点的距离。

（二）、确定单形（Simplicial subdivision）。

  在前面的学习中，我们知道，一个３维超晶格体由六个３维单形构成，因此，相对二维需要判断输入点处于两个等边三角形中的一个，３维中我们需要判断输入点处于六个３维单形中的一个。如下简化的平面图示：

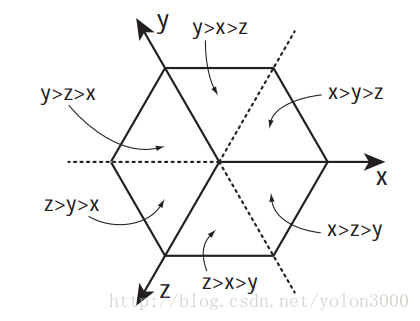
  相对二维，三维的实施过程要复杂得多（也正因为如此，四维时我们将换一种方法实现），但只要理解了原理，代码还是比较容易实现，代码如下：

            int I1, J1, K1;
            int I2, J2, K2;
            if (dx0 >= dy0)
            {
                if (dy0 >= dz0)
                { I1 = 1; J1 = 0; K1 = 0; I2 = 1; J2 = 1; K2 = 0; }
                else if (dx0 >= dz0) { I1 = 1; J1 = 0; K1 = 0; I2 = 1; J2 = 0; K2 = 1; }
                else { I1 = 0; J1 = 0; K1 = 1; I2 = 1; J2 = 0; K2 = 1; }
            }
            else
            {
                if (dy0 < dz0) { I1 = 0; J1 = 0; K1 = 1; I2 = 0; J2 = 1; K2 = 1; }
                else if (dx0 < dz0) { I1 = 0; J1 = 1; K1 = 0; I2 = 0; J2 = 1; K2 = 1; }
                else { I1 = 0; J1 = 1; K1 = 0; I2 = 1; J2 = 1; K2 = 0; }
            }

（三）、梯度值选择（Gradient selection）。

  与Perlin噪声实现一样，选取梯度索引值，同时我们还求出了输入点到各顶点的距离值。

            double dx1 = dx0 - I1 + G3;
            double dy1 = dy0 - J1 + G3;
            double dz1 = dz0 - K1 + G3;
            double dx2 = dx0 - I2 + 2.0 * G3;
            double dy2 = dy0 - J2 + 2.0 * G3;
            double dz2 = dz0 - K2 + 2.0 * G3;
            double dx3 = dx0 - 1.0 + 3.0 * G3;
            double dy3 = dy0 - 1.0 + 3.0 * G3;
            double dz3 = dz0 - 1.0 + 3.0 * G3;

            int indexI = I0 & 255;
            int indexJ = J0 & 255;
            int indexK = K0 & 255;
            int g0 = p[indexI + p[indexJ + p[indexK]]] & 0xF;
            int g1 = p[indexI + I1 + p[indexJ + J1 + p[indexK + K1]]] & 0xF;
            int g2 = p[indexI + I2 + p[indexJ + J2 + p[indexK + K2]]] & 0xF;
            int g3 = p[indexI + 1 + p[indexJ + 1 + p[indexK + 1]]] & 0xF;

（四）、求和（Kernel summation）。

  求和过程很简单，最后我们将和乘32是归一化[－１，１]中。

return 32.0 * (n0 + n1 + n2 + n3);

  最后生成的图像如下，我们将第三维作为时间输入，可以到了平面的动画效果(录像的原因，实际动画很平滑)。

二、4D Simplex Noise

  ４D Simplex 噪声与3D Simplex噪声类似，实现步骤都一样，这里只给出关键代码，理解了3D Simplex噪声，4D Simplex实现也就不难了，但这次我们确定单形时使用了另外不同的方法（因为确定输入点所在单形变得比3D更加复杂了）。

（一）、坐标变换（Coordinate skewing）。

            double F4 = (Math.Sqrt(5.0) - 1.0) / 4.0;
            double G4 = (5.0 - Math.Sqrt(5.0)) / 20.0;
            double n0, n1, n2, n3, n4; 

            double s = (x + y + z + w) * F4; 
            int I0 = GetFloor(x + s);
            int J0 = GetFloor(y + s);
            int K0 = GetFloor(z + s);
            int L0 = GetFloor(w + s);

            double t = (I0 + J0 + K0 + L0) * G4; 
            double i0 = I0 - t; 
            double j0 = J0 - t;
            double k0 = K0 - t;
            double l0 = L0 - t;

（二）、确定单形（Simplicial subdivision）。

  确定输入点所在的单形，为避免过多的if else判断，我们的思路是精心设计好一个simplexOrder查找表，这个表根据输入的特定条件直接返回对应的正超晶格顶点多坐标，前人已经为我们设计好了一个这样的表，我们只需要根据条件去查找表里找即可，代码看起来比较难理解，但其本质其实也是根据条件区分情况处理。

            int c1 = (dx0 > dy0) ? 32 : 0;
            int c2 = (dx0 > dz0) ? 16 : 0;
            int c3 = (dy0 > dz0) ? 8 : 0;
            int c4 = (dx0 > dw0) ? 4 : 0;
            int c5 = (dy0 > dw0) ? 2 : 0;
            int c6 = (dz0 > dw0) ? 1 : 0;
            int c = c1 + c2 + c3 + c4 + c5 + c6;

            int I1, J1, K1, L1; 
            int I2, J2, K2, L2; 
            int I3, J3, K3, L3; 

            I1 = simplexOrder[c,0] >= 3 ? 1 : 0;
            J1 = simplexOrder[c,1] >= 3 ? 1 : 0;
            K1 = simplexOrder[c,2] >= 3 ? 1 : 0;
            L1 = simplexOrder[c,3] >= 3 ? 1 : 0;

            I2 = simplexOrder[c,0] >= 2 ? 1 : 0;
            J2 = simplexOrder[c,1] >= 2 ? 1 : 0;
            K2 = simplexOrder[c,2] >= 2 ? 1 : 0;
            L2 = simplexOrder[c,3] >= 2 ? 1 : 0;

            I3 = simplexOrder[c,0] >= 1 ? 1 : 0;
            J3 = simplexOrder[c,1] >= 1 ? 1 : 0;
            K3 = simplexOrder[c,2] >= 1 ? 1 : 0;
            L3 = simplexOrder[c,3] >= 1 ? 1 : 0;

（三）、梯度值选择（Gradient selection）。

  梯度选择与4D Perlin噪声选取梯度索引一样。

            int g0 = p[indexI +      p[indexJ +      p[indexK +      p[indexL]]]] % 0x1F;
            int g1 = p[indexI + I1 + p[indexJ + J1 + p[indexK + K1 + p[indexL + L1]]]] % 0x1F;
            int g2 = p[indexI + I2 + p[indexJ + J2 + p[indexK + K2 + p[indexL + L2]]]] % 0x1F;
            int g3 = p[indexI + I3 + p[indexJ + J3 + p[indexK + K3 + p[indexL + L3]]]] % 0x1F;
            int g4 = p[indexI + 1 +  p[indexJ + 1 +  p[indexK + 1 +  p[indexL + 1]]]] % 0x1F;

（四）、求和（Kernel summation）。

  求和过程也一样，最后我们将和乘27.0归一化到[－１，１]中。生成的以时间为第三个维度，第四个维度是定值的Simplex噪声图像如下：

三、代码下载

VS2015平台下用C#实现的Simplex噪声：
VS2015_C#_Simplex噪声

Unity2017.1.1f1+cg版
这个版本我目前只实现了２D Simplex噪声，这是因为在我实现２D噪声后发现了一些问题，生成的单形边界很明显，特别是在使用分形后，可以明显的看出单形形状，目前我还没有找到问题的原因，解决后３D、4D一并放出。
Unity2017.1.1f1_Cg_SimplexNoise2D

参考文献

Simplex noise demystified，Stefan Gustavson, Linköping University, Sweden (stegu@itn.liu.se), 2005-03-22