从渲染管线学 GLES2.0（三）----变换（MVP变换）

光头小杨

已于 2024-04-22 16:29:54 修改

阅读量1k

点赞数 13

分类专栏： OpenGL ES 2.0 文章标签： OpenGL ES 2.0

于 2024-04-02 13:50:20 首次发布

本文链接：https://blog.csdn.net/yp18792574062/article/details/137255712

版权

OpenGL ES 2.0 专栏收录该内容

9 篇文章 0 订阅

订阅专栏

在看变换之前，我们先来看一些变换过程中所需要的数学知识，也就是向量和矩阵，以及它们的各种运算

1、向量

1.1 向量定义

向量最基本的定义就是一个方向，或者更正式的说，向量有一个方向和大小。如果一个向量有两个维度，它表示一个平面的方向，当它有 3 个维度的时候它可以表达一个 3D 世界的方向。比如下面就表示一个平面向量。

对于三维向量来讲，一般我们会使用字母上面加一横表示向量，当用在公式时它们通常是这样的

$\overline{v} = \begin{pmatrix} x\\ y\\ z\\ \end{pmatrix}$

由于向量是一个方向，所以有些时候很难形象的将它们用位置表示出来。为了让其更加直观，我们通常设定这个方向的原点为(0, 0, 0)，然后指向一个方向。比如说位置向量(3, 2)在图像中的起点是(0, 0)，并且指向(3, 2)。我们可以使用向量在2D或3D空间中表示方向和位置

1.2 向量和标量的运算

标量只是一个数字。当我们把向量加减乘除一个标量。可以简单的把向量的每个分量进行进行该运算，对于加法来说像这样

$\begin{pmatrix} 1\\ 2\\ 3\\ \end{pmatrix} + x = \begin{pmatrix} 1+x\\ 2+x\\ 3+x\\ \end{pmatrix}$

1.3 向量长度

我们使用勾股定理来获取向量的长度，对于向量 v 来讲

$\overline{v} = \begin{pmatrix} x\\ y\\ z\\ \end{pmatrix}$

它的长度计算就像下面这样

$\|\overline{v}\| = \sqrt{\smash[b]{x^{\smash{2}} + y^{\smash{2}} + z^{\smash{2}}}}$

1.4 向量加减

向量的加减可以被定义为是每个分量的加减，比如下面这样

$\begin{pmatrix} 1\\2\\3\\ \end{pmatrix} + \begin{pmatrix} 4\\5\\6\\ \end{pmatrix} = \begin{pmatrix} 1+4\\2+5\\3+6\\ \end{pmatrix} = \begin{pmatrix} 5\\7\\9\\ \end{pmatrix}$

1.5 向量相乘

两个向量相乘是一种很奇怪的情况，普通的乘法在向量上是没有定义的，因为它在视觉上是没有意义的。但是在相乘的时候有两种特定的情况可以选择，一个是点乘(dot)，一个是叉乘(cross)

点乘

两个向量的点乘等于它们的数乘结果乘以两个向量夹角的余弦值。

$\overline{v}\cdot\overline{w}=\|\overline{v}\|\cdot\|\overline{w}\|\cdot\cos\theta$

当两个向量都是单位向量时，它们的长度都等于1，那么点乘可以很容易的测试两个向量之间的位置关系

点乘是通过将对应分量逐个相乘，然后再把所得的结果加起来的，点乘会像下面这样

$\begin{pmatrix} 0.6\\0.8\\0\\ \end{pmatrix} \cdot \begin{pmatrix} 0\\1\\0\\ \end{pmatrix} = \left(0.6*0\right) + \left(0.8*1\right) + \left(0*0\right) = 0.8$

叉乘

两个向量的叉乘又叫向量积，叉乘的运算结果也是一个向量，比如下面这样

$\begin{pmatrix} \mathnormal{Ax}\\ \mathnormal{Ay}\\ \mathnormal{Az}\\ \end{pmatrix} \times \begin{pmatrix} \mathnormal{Bx}\\ \mathnormal{By}\\ \mathnormal{Bz}\\ \end{pmatrix} = \begin{pmatrix} \mathnormal{Ay}\cdot\mathnormal{Bz}- \mathnormal{Az}\cdot\mathnormal{By}\\ \mathnormal{Az}\cdot\mathnormal{Bx}- \mathnormal{Ax}\cdot\mathnormal{Bz}\\ \mathnormal{Ax}\cdot\mathnormal{By}- \mathnormal{Ay}\cdot\mathnormal{Bx} \end{pmatrix}$

在 3D 图形中，叉乘的概念非常有用，可以通过两个向量的叉乘，生成第三个垂直于前两个向量的法向量。

2、矩阵

2.1 矩阵定义

简单来说矩阵就是一个矩形的数字、符号或者表达式数组。矩阵中的每一项叫做矩阵的元素，下面是一个2x3矩阵的例子

$\begin{bmatrix} 1&2&3\\ 4&5&6\\ \end{bmatrix}$

矩阵可以通过(i, j)索引，i 是行，j 是列。

2.2 矩阵和标量的加法

标量值要加到矩阵的每一个元素上，减法、乘法、除法都是类似的，比如下面这样

$\begin{bmatrix} 1&2\\ 4&5\\ \end{bmatrix} + 3 = \begin{bmatrix} 1+3&2+3\\ 4+3&5+3\\ \end{bmatrix}= \begin{bmatrix} 4&5\\ 7&8 \end{bmatrix}$

2.3 矩阵和矩阵的加法

矩阵和矩阵之间的加减就是两个矩阵对应元素的加减操作，和矩阵和标量的运算是差不多的，只不过相同索引下的元素才能进行计算。

$\begin{bmatrix} 1&2\\ 3&4\\ \end{bmatrix}+ \begin{bmatrix} 5&6\\ 7&8\\ \end{bmatrix}= \begin{bmatrix} 1+5&2+6\\ 3+7&4+8 \end{bmatrix}= \begin{bmatrix} 6&8\\ 10&12\\ \end{bmatrix}$

2.4 矩阵和矩阵的乘法

矩阵乘法基本上意味着遵照规定好的法则进行相乘，当然相乘还是有一些限制的

1. 只有当左侧矩阵的列数和右侧矩阵的行数相等，两个矩阵才可以相乘

2. 矩阵相乘不满足交换律，也就是矩阵A乘矩阵B，不等于矩阵B乘矩阵A

比如我们看一个 2x3 的矩阵和一个 3x2 的矩阵相乘的例子，结果是一个 2x2 的矩阵

$\begin{bmatrix} 1&2&3\\ 4&5&6\\ \end{bmatrix}\times \begin{bmatrix} 7&8\\ 9&10\\ 11&12 \end{bmatrix}= \begin{bmatrix} 1*7+2*9+3*11&1*8+2*10+3*12\\ 4*7+5*9+6*11&4*8+5*10+6*12 \end{bmatrix}= \begin{bmatrix} 58&64\\ 129&154\\ \end{bmatrix}$

也就是第一个向量的每一行和第二个矩阵的每一列相乘

2.5 矩阵和向量的乘法

矩阵和向量的乘法也是不满足交换律的，我们一般使用的场景都是矩阵乘向量

矩阵乘向量

矩阵的每一行和向量的一列进行相乘，乘完还是一个向量。

$\begin{bmatrix} 1&2&3\\ 4&5&6\\ 7&8&9\\ \end{bmatrix} * \begin{bmatrix} 20\\ 21\\ 22\\ \end{bmatrix}= \begin{bmatrix} 1*20+2*21+3*22\\ 4*20+5*21+6*22\\ 7*20+8*21+9*22\\ \end{bmatrix}= \begin{bmatrix} 128\\ 317\\ 506\\ \end{bmatrix}$

向量乘矩阵

向量的一行和矩阵的每一列进行相乘，乘完还是一个向量。

$\begin{bmatrix} 20&21&22\\ \end{bmatrix}* \begin{bmatrix} 1&2&3\\ 4&5&6\\ 7&8&9\\ \end{bmatrix}\\= \begin{bmatrix} 20*1+21*4+22*7& 20*2+21*5+22*8& 20*3+21*6+22*9\\ \end{bmatrix} \\= \begin{bmatrix} 258&321&384\\ \end{bmatrix}$

2.6 单位矩阵

在 OpenGL 中，我们通常会使用4x4的变换矩阵，而其中最主要的原因就是大部分的向量都是4分量的，我们能想到的最简单的变换矩阵就是单位矩阵了，单位矩阵是一个除了对角线以外都是0的矩阵，单位矩阵和向量相乘，还是向量本身，可以使得向量不做变换

$\begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} * \begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}= \begin{bmatrix} 1*1\\ 1*2\\ 1*3\\ 1*4\\ \end{bmatrix}= \begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}$

3、 MVP 变换

3.1 什么是 MVP 变换

MVP 变换就是我们常说的模型（Model）、视图（View）、投影（Projection）变换三个单词的缩写。

3.2 局部空间

以原点(0, 0, 0)为模型起始点的空间，就称为局部空间，比如我们使用应用程序中写的点坐标就在局部空间中

3.2 世界空间（模型变换）

局部空间的坐标经过平移（transform）、旋转（rotate）、缩放（scale）等操作后，坐标就到了世界空间。其中平移、旋转、缩放操作我们称为模型变换。模型变换就是把物体模型从其本身的坐标系中拿出来，转换到整个场景的坐标系中，也就是世界空间中。模型变换一般都是先进行线性变换（缩放、旋转），然后再是平移，因为矩阵的相乘是不满足交换律的，如果先位移再缩放，那么位移的向量也同样会被缩放，所以一般的顺序是先缩放、再旋转、最后平移。

缩放矩阵

对一个向量进行缩放就是对向量的长度进行缩放，而保持它的方向不变。一般情况下，我们会构造一个缩放矩阵来提供缩放功能，从上面的单位矩阵可以看到，每个对角线元素会分别与向量的对应元素相乘。如果我们把缩放变量表示为(S1, S2, S3)我们可以为任意向量(x, y, z)定义一个缩放矩阵

$\begin{bmatrix} S1&0&0&0\\ 0&S2&0&0\\ 0&0&S3&0\\ 0&0&0&1\\ \end{bmatrix} * \begin{bmatrix} x\\ y\\ z\\ 1\\ \end{bmatrix}= \begin{bmatrix} S1*x\\ S2*y\\ S3*z\\ 1\\ \end{bmatrix}$

旋转矩阵

旋转矩阵在 3D 空间中每个单位轴都有不同的定义，旋转角度用 $a$ 表示

按照 x 轴旋转

$\begin{bmatrix} 1&0&0&0\\ 0&cos(a)&-sin(a)&0\\ 0&sin(a)&cos(a)&0\\ 0&0&0&1\\ \end{bmatrix}$

按照 y 轴旋转

$\begin{bmatrix} cos(a)&0&sin(a)&0\\ 0&1&0&0\\ -sin(a)&0&cos(a)&0\\ 0&0&0&1\\ \end{bmatrix}$

按照 z 轴旋转

$\begin{bmatrix} cos(a)&-sin(a)&0&0\\ sin(a)&cos(a)&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix}$

平移矩阵

平移是在原始向量的基础上加上另一个向量从而获得一个在不同位置的新向量的过程，从而在平移向量基础上移动了原始向量

$\begin{bmatrix} 1&0&0&tx\\ 0&1&0&ty\\ 0&0&1&tz\\ 0&0&0&1\\ \end{bmatrix}* \begin{bmatrix} x\\ y\\ z\\ 1\\ \end{bmatrix}= \begin{bmatrix} x + tx\\ y + ty\\ z + tz\\ 1\\ \end{bmatrix}$

一个先进行缩放，再进行旋转、平移后的模型矩阵就像下面这样，矩阵和向量的相乘顺序是从右向左。

mode = transform * rotate * scale

3.2 观察空间（视图变换）

观察矩阵就是将物体在世界空间的坐标变换到观察空间的矩阵，观察空间需要一个观察者作为参考对象，一般来说都是摄像机。摄像机在世界空间内某个坐标观察场景中的物体，观察空间就是摄像机看到的视图空间。

观察空间都有一个特征，就是观察者始终处于坐标原点，且面向 -Z 轴，这是为了后续方便计算，以便可以将观察者看到的任何物体变换看成是在观察空间内相对于坐标原点的变换，即在观察空间内，观察者就是原点。一般情况下，我们要把观察者往后移，那么就相当于物体往前移一样。

观察空间一般的操作也就是平移和旋转操作，平移和旋转矩阵在上面也都提到过。这里也就不再单独的介绍。

3.3 裁剪空间（投影变换）

在一个顶点着色器运行的最后，我们期望所有的坐标都能落在一个特定的范围内，且任何在这个范围之外的点都应该被裁剪掉，裁剪掉的坐标就会被忽略，所以剩下的坐标就将变为屏幕上可见的片段，这也就是裁剪空间名字的由来。

为了将顶点坐标从观察变换到裁剪空间，我们需要定义一个投影矩阵，它指定了一个范围坐标，比如我们在每个维度上指定范围坐标为 [-1000, 1000]，投影矩阵就会将在这个指定的范围内的坐标变换为标准化坐标的范围内[-1.0, 1.0]，所有在范围外的坐标不会被映射到 -1.0 到 1.0 的范围之间，所以会被裁剪掉。

由投影矩阵创建的观察箱被称为平截头体，每个出现在平截头体范围内的坐标最终都会出现在用户的屏幕上。将特定范围内的坐标转换到标准化坐标的过程称为投影，因为使用投影矩阵能将 3D 坐标投影很容易映射到 2D 标准化设备坐标系中。

标准视体

标准视体中的坐标就是标准设备坐标，就是将 xyz 坐标都划分在 [-1, 1] 的区间之内，框出来一个从直观上看起来很标准的立方体空间。

正交投影

正交投影也叫正射投影，它定义了一个类似立方体的平截头箱，在这空间之外的顶点都会被裁剪掉，一个正交投影的盒子就像下面这样

如上图所示，坐标原点认为是观察者的位置，正交投影框出了一个空间区域，表示我们现在要渲染的是这个空间区域内的物体，其中正交投影的左右下上近远平面分别用l(left)、r(right)、b(bottom)、t(top)、n(near)、f(far)来表示。

在 GLM 中可以创建一个正交投影矩阵

glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);

前两个参数指定了平截头体的左右坐标，第三第四参数制定了平截头的底部和顶部，最后两个参数制定了近平面和远平面的距离。

透视投影

在正常情况下，离我们近的物体看起来比较大，离我们远的物体看起来比较小，也就是常说的近大远小的效果，这个效果被称为透视。

要实现透视的效果，我们需要使用到透视投影矩阵，这个矩阵将给定的平截头体范围映射到裁剪空间，除此之外透视变换还会修改每个顶点的 w 值，从而使得观察者越远的顶点坐标 w 分量越大。

在 GLM 中可以创建一个透视投影矩阵

glm::mat4 proj = glm::perspective(glm::radians(45.0f), (float)width/(float)height, 0.1f, 100.0f);

第一个参数 fov 表示的是一个视野，它的值通常设置为45.0f，但想要一个末日风格的结果你可以将其设置一个更大的值。第二个参数设置了一个宽高比 aspect，由视口的宽除以高所得。第三和第四个参数设置了平截头体的近和远平面，我们通常设置近距离为0.1f，而远距离设为100.0f。当你把透视矩阵的 near 值设置太大时（如10.0f），OpenGL会将靠近摄像机的坐标（在0.0f和10.0f之间）都裁剪掉，这会导致一个你在游戏中很熟悉的视觉效果：在太过靠近一个物体的时候你的视线会直接穿过去。

其实 glm::perspective 做的就是创建了一个可视空间的大平截头体，任何在这个平截头体的东西都会被裁剪掉。一个透视平截头体可以被看作一个不均匀形状的箱子，在这个箱子内部的每个坐标都会被映射到裁剪空间上的一个点。下面是一张透视平截头体的图片：

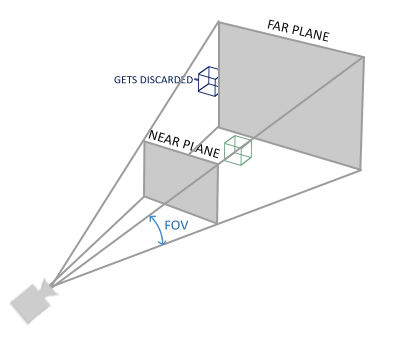
一般的透视矩阵为

$\begin{bmatrix} 1\over(aspect * tan(fov/2))&0&0&0\\ 0&1\over(tan(fov/2))&0&0\\ 0&0&(near+far)\over(near-far)&(2*near*far)\over(near-far)\\ 0&0&-1&0\\ \end{bmatrix}$

3.4 透视除法（NDC坐标）

透视除法将裁剪空间的顶点的 4 个分量都除以 w，就从裁剪空间转换到 NDC 了。NDC 坐标盒子也就是标准视体的盒子。

3.5 屏幕空间

NDC 标准设备坐标经过视窗变换后的坐标就到了屏幕空间

视窗变换矩阵

$\begin{bmatrix} {width \over 2}&0&0&{width \over 2}\\ 0&{height \over 2}&0&{height \over 2}\\ 0&0& {far-near \over 2}& {far+near \over 2}\\ 0&0&0&1\\ \end{bmatrix} * \begin{bmatrix} x\\y\\z\\1 \end{bmatrix} = \begin{bmatrix} {width \over 2}*x+{width \over 2}\\ {height \over 2}*y+{height \over 2}\\ {far-near \over 2}*z+ {far+near \over 2}\\ 1\\ \end{bmatrix}$

现在的 MVP 变换都是在顶点着色器中做处理的，因为进入到裁剪空间，我们要把一些顶点做裁剪掉，所以接下来我们重点会说如何把这些顶点裁剪掉。

4、参考文章

坐标系统 - LearnOpenGL CN

图形学：MVP变换概述 - 知乎

图形学：正交/透视投影矩阵的推导（多个思路） - 知乎

光头小杨

关注

13
点赞
踩
20

收藏

觉得还不错? 一键收藏
0
评论
从渲染管线学 GLES2.0（三）----变换（MVP变换）

向量最基本的定义就是一个方向，或者更正式的说，向量有一个方向和大小。如果一个向量有两个维度，它表示一个平面的方向，当它有 3 个维度的时候它可以表达一个 3D 世界的方向。比如下面就表示一个平面向量。对于三维向量来讲，一般我们会使用字母上面加一横表示向量，当用在公式时它们通常是这样的由于向量是一个方向，所以有些时候很难形象的将它们用位置表示出来。为了让其更加直观，我们通常设定这个方向的原点为(0, 0, 0)，然后指向一个方向。
复制链接

扫一扫