滑块沿光滑不固定的斜面下滑,在到达斜面底端时的情况。
设滑块质量m,斜面质量M,斜面高度h,倾角α,它们之间压力大小N,到达底端所用时间t。
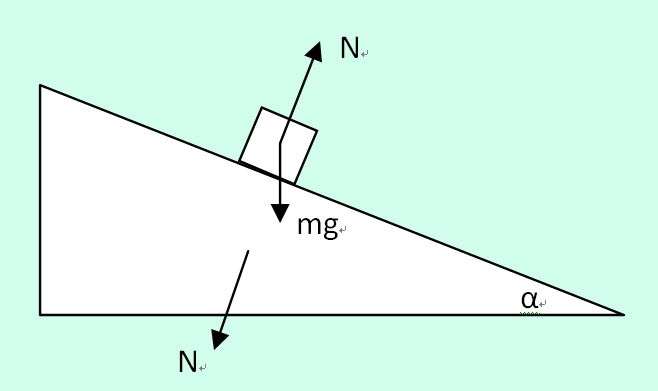
受力分析
(斜面重力和所受地面支持力对题目无影响,故忽略)
物体受力:
Fy=mg-Ncosα 竖直向下
Fx=Nsinα 水平向右
使斜面运动的力:
Fx=Nsinα 水平向左
物体:
在斜面上滑动的竖直距离为h,水平距离为
竖直加速度
因为 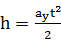
水平加速度
设物体水平移动的实际距离s,向右为正
斜面:
水平加速度
设水平移动距离为SM,向左为正
物体水平移动实际距离=在斜面移动水平距离-斜面移动距离,即
即
得
设物体水平速度Vx
竖直速度Vy
斜面水平速度VMx
现在检验一下Vx VMx
水平方向动量守恒 mVx =MVMx
代入上面的Vx VMx,等式成立,即没算错。
由动能定理
物体获得的动能
或
用(1)算
①化为
①化为
用(2)算
①化为
(1)和(2)算出的结果一样,所以没算错。
结论:有两个倾角不同、高度相同、质量一样的斜面放在光滑的水平面上,斜面是光滑的,有两个一样的物块分别从两个斜面的顶点由静止开始滑下,则物块到达斜面底端时的动能不相等。







 本文详细分析了滑块沿光滑不固定的斜面下滑时的受力情况,包括竖直加速度、水平加速度以及物体与斜面间的作用力。通过动力学原理,推导出物体到达斜面底端时的动能与倾角的关系,最终得出在不同倾角下,具有相同质量和高度的斜面,其滑块到达底端时的动能并不相等的结论。
本文详细分析了滑块沿光滑不固定的斜面下滑时的受力情况,包括竖直加速度、水平加速度以及物体与斜面间的作用力。通过动力学原理,推导出物体到达斜面底端时的动能与倾角的关系,最终得出在不同倾角下,具有相同质量和高度的斜面,其滑块到达底端时的动能并不相等的结论。
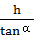
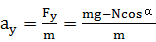
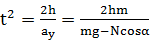


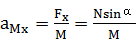
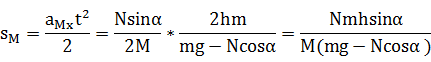
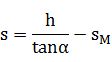
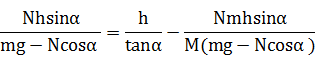
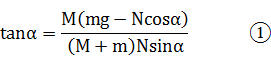
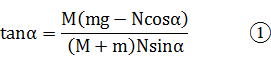
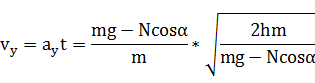
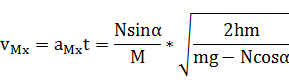
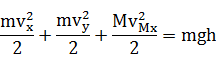
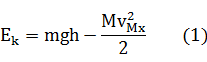
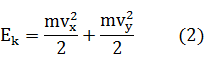
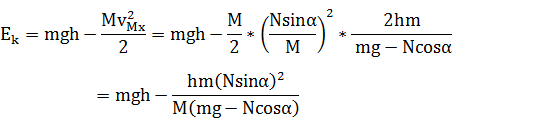
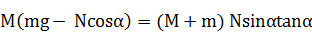
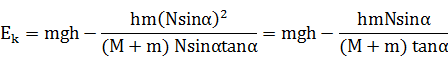
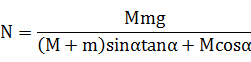

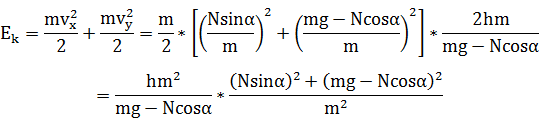
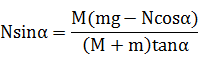

















 2052
2052

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








