【MATLAB】平滑处理

从现实环境采集到的数据中经常混叠有微弱噪声,其中包括由于系统不稳定产生的噪声，也有周围环境引入的毛刺,这些弱噪声都需要在处理信号之前尽可能地消除或减弱。这一工作往往作为预处理的一部分。在本节中将通过案例介绍几种简单又实用的平滑处理方法:五点三次平滑法、MATLAB自带平滑处理的smooth函数和Savitzky-Golay平滑滤波器等。

五点三次平滑法

1.概 述

对于带毛刺或弱噪声的数据经常会采用五点三次平滑法来进行平滑处理。给出了相应的MATLAB程序,这里编写成如下函数mean5_3:函数:mean5 3；功能:对数据进行五点三次平滑处理

调用格式:y=mean5 3(x,m)

说明:x是要平滑的输入序列,m是对数据进行多次循环平滑的次数;y是平滑后的输出序列。数据x能进行多次五点三次的平滑处理,但m必须选择一个适当的值,不宜太大,否则容易使峰值降低,峰值频带变宽。

function y=mean5_3(x,m)
% x为被处理的数据
% m 为循环次数
n=length(x);
  a=x;
  for k=1: m
     b(1) = (69*a(1) +4*(a(2) +a(4)) -6*a(3) -a(5)) /70;
     b(2) = (2* (a(1) +a(5)) +27*a(2) +12*a(3) -8*a(4)) /35;
     for j=3:n-2
       b (j) = (-3*(a(j-2) +a(j+2)) +12*(a(j-1) +a(j+1)) +17*a(j)) /35;
     end
     b (n-1) = (2*(a(n) +a(n-4)) +27*a(n-1) +12*a(n-2) -8*a(n-3)) /35;
     b (n) = (69*a(n) +4* (a(n-1) +a(n-3)) -6*a(n-2) -a(n-4)) /70;
     a=b;
  end
  y =a;

有一组带噪信号数据文件xnoisedata.txt,数据的第1列是时间,第2列是实验检测到的数据。由于环境的原因,实验数据中含有噪声,要求通过平滑方法对数据进行处理。本例采用五点三次平滑法,程序清单如下：

clear all; clc; close all;
xx=load('xnoisedata1.txt');     % 读入数据
time=xx(:,1);                   % 时间序列
x=xx(:,2);                      % 带噪数据
xmean=mean5_3(x,50);            % 调用mean5_3函数,平滑数据
% 作图
subplot 211; plot(time,x,'k');
xlabel('时间/s'); ylabel('幅值')
title('原始数据'); xlim([0 max(time)]);
subplot 212; plot(time,xmean,'k'); 
xlabel('时间/s'); ylabel('幅值')
title('平滑处理后的数据'); xlim([0 max(time)]);
set(gcf,'color','w');

在带噪数据中如何寻找极小值

——介绍 MATLAB自带的平滑函数smooth

1.概 述

本案例主要介绍MATLAB自带的平滑函数smooth。在日常数字信号处理中经常会要寻找极大(小)值,但在有噪声的情况下很难找到实际数据的极大(小)值,所以对于带噪数据先得对数据进行平滑,平滑以后再来寻找极大(小)值。在本小节中将以寻找极小值为例来介绍MATLAB自带的平滑函数smooth的应用。

3.MATALB自带的平滑函数smooth

名称:smooth；功能:对一维信号进行平滑处理

调用格式:
y= smooth(x)
y= smooth(x,SPAN)
y= smooth(x,SPAN,method)

说明:x是被平滑处理的输入数据,SPAN是平滑处理中取的窗长(取奇数)。y是平滑处理后的输出数据。Method是平滑处理的方法,共有6种,见表。

‘moving'方法的理论如前面理论基础中所介绍的,sgolay'是使用Savitzky-Golay方法的滤波器

2.实例

有一个整周期的余弦信号,但叠加了噪声,要求寻找余弦信号极小值的位置和幅值。调用MATLAB自带的smooth函数试验不同的参数,程序清单如下:

clear all; clc; close all;
k=1:500;                    % 产生一个从0到2*pi的向量，长为500               
dn=2*pi/500;
x=cos((k-1)*dn);            % 产生一个周期余弦信号
[val,loc]=min(x);           % 求出余弦信号中的最小值幅值和位置
N=length(x);                % 数据长
ns=randn(1,N);              % 产生随机信号
y=x+ns(1:N)*0.1;            % 构成带噪信号
Err=var(x-y);               % 求x-y的方差
fprintf('%4d   %5.4f   %5.6f\n',loc,val,Err);
y=y';                       % 转成列向量
z1=smooth(y,51,'moving');   % 'moving'平滑
Err1=var(x'-z1);            % 求x-z1的方差 
[v1,k1]=min(z1);            % 求出平滑信号z1中的最小值幅值和位置
fprintf('1  %4d   %5.4f   %4d   %5.6f\n',k1,v1,abs(loc-k1),Err1);  % 显示
z2=smooth(y,51,'lowess');   % 'lowess'平滑
Err2=var(x'-z2);            % 求x-z2的方差
[v2,k2]=min(z2);            % 求出平滑信号z2中的最小值幅值和位置
fprintf('2  %4d   %5.4f   %4d   %5.6f\n',k2,v2,abs(loc-k2),Err2);
z3=smooth(y,51,'loess');    % 'loess'平滑
Err3=var(x'-z3);            % 求x-z3的方差
[v3,k3]=min(z3);            % 求出平滑信号z3中的最小值幅值和位置
fprintf('3  %4d   %5.4f   %4d   %5.6f\n',k3,v3,abs(loc-k3),Err3);
z4=smooth(y,51,'sgolay',3); % 'sgolay'平滑
Err4=var(x'-z4);            % 求x-z4的方差
[v4,k4]=min(z4);            % 求出平滑信号z4中的最小值幅值和位置
fprintf('4  %4d   %5.4f   %4d   %5.6f\n',k4,v4,abs(loc-k4),Err4);
z5=smooth(y,51,'rlowess');  % 'rlowess'平滑
Err5=var(x'-z5);            % 求x-z5的方差
[v5,k5]=min(z5);            % 求出平滑信号z5中的最小值幅值和位置
fprintf('5  %4d   %5.4f   %4d   %5.6f\n',k5,v5,abs(loc-k5),Err5);
z6=smooth(y,51,'rloess');   % 'rloess'平滑
Err6=var(x'-z6);            % 求x-z6的方差
[v6,k6]=min(z6);            % 求出平滑信号z6中的最小值幅值和位置
fprintf('6  %4d   %5.4f   %4d   %5.6f\n',k6,v6,abs(loc-k6),Err6);
% 作图
subplot 211; plot(k,x,'k');
grid; xlim([0 500]); title('一周期余弦信号')
xlabel('样点'); ylabel('幅值')
subplot 212; plot(k,y,'k'); %hold on
grid; axis([0 500 -1.5 1.5]); title('带噪一周期余弦信号')
xlabel('样点'); ylabel('幅值')
set(gcf,'color','w');
figure
subplot 321; plot(k,z1,'k'); title('moving法')
grid; axis([0 500 -1.5 1.5]); ylabel('幅值')
subplot 322; plot(k,z2,'k');  title('lowess法')
grid; axis([0 500 -1.5 1.5]); ylabel('幅值')
subplot 323; plot(k,z3,'k'); title('loess法')
grid; axis([0 500 -1.5 1.5]); ylabel('幅值')
subplot 324; plot(k,z4,'k'); title('sgolay法')
grid; axis([0 500 -1.5 1.5]); ylabel('幅值')
subplot 325; plot(k,z5,'k'); title('rlowess法')
grid; axis([0 500 -1.5 1.5]); xlabel('样点'); ylabel('幅值')
subplot 326; plot(k,z6,'k'); title('rloess法')
grid; axis([0 500 -1.5 1.5]); xlabel('样点'); ylabel('幅值')
set(gcf,'color','w');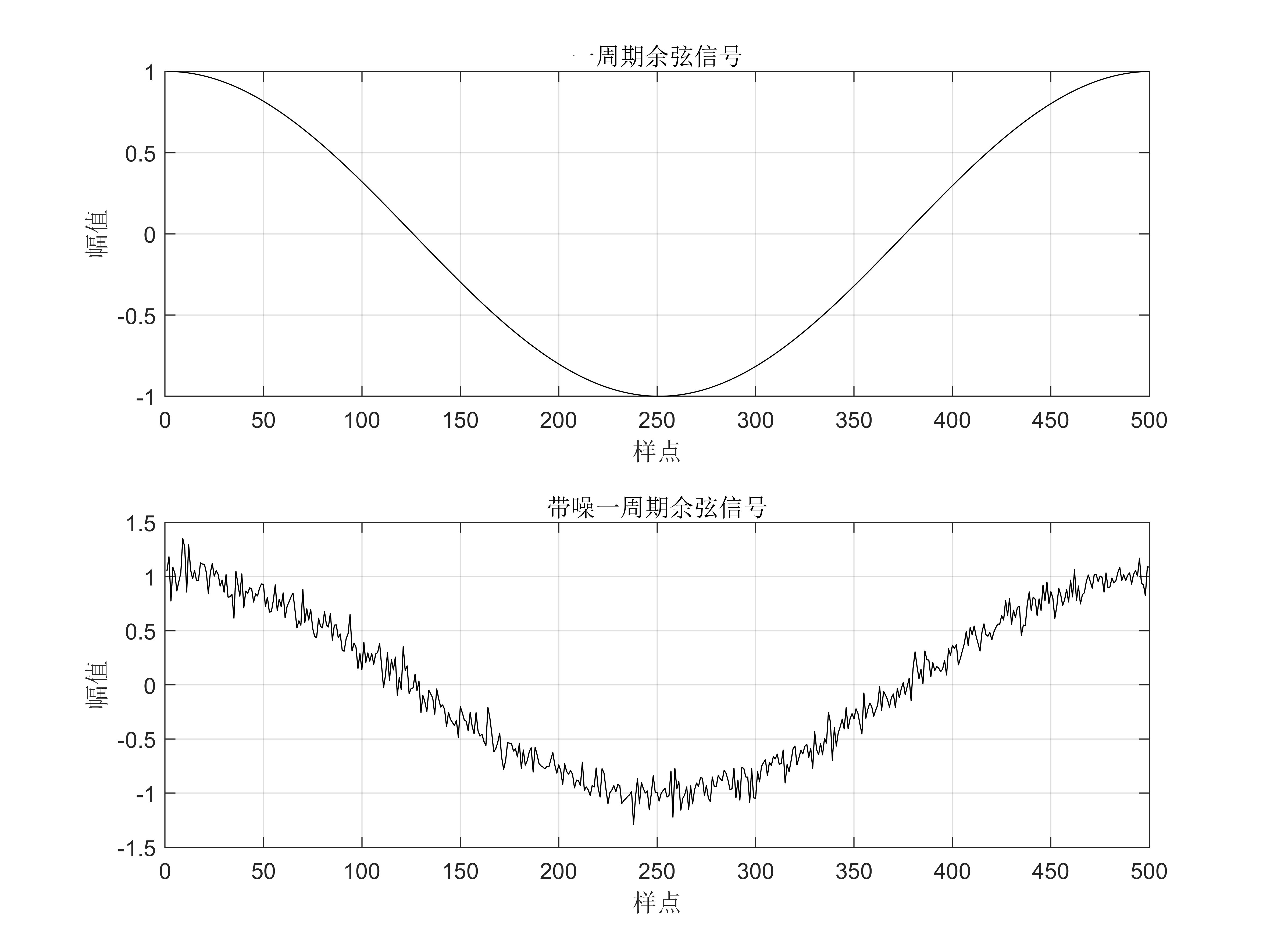

 Savitzky-Golay平滑滤波

1.概 述

一般在平滑处理中,窗长不宜过大。SavitzkyA和GolayM在1964年提出了一种基于多项式拟合的方法来设计最佳且形式简单的低通滤波器,这种滤波器称为Savitzky-Golay平滑器,该平滑器允许窗长可以较大,且对于大部分数据的平滑都比较有效。

2.MATLAB 中自带的Savitzky-Golay平滑滤波函数

在MATLAB中自带了两个与Savitzky-Golay平滑滤波有关的函数,现介绍如下(1)求 Savitzky-Golay 滤波器系数

名称:sgolay功能:设计低通滤波器求其系数

调用格式:b=sqolay(k.f)

说明:输入参数k是多项式拟合中的阶数,f是窗长,该值必须为奇数。输出参数b是Savitzky-Golay法的FIR平滑滤波器

(2)实现Savitzky-Golay 滤波

名称:sgolayfilt

功能:实现Savitzky-Golay 滤波

调用格式:y=sgolayfilt(x,k,f)

说明:输入参数x是输人信号,k是多项式拟合中的阶数,f是窗长,该值必须为奇数。输出参数y是FIR滤波器输出。

3.实 例

设正弦信号的采样频率为5Hz,信号频率为0.2Hz,长200s,在信号中混入了噪声,用Savitzky-Golay滤波器平滑该正弦信号。程序清单如下:

clear all; clc; close all;
t=0:.2:199;            % 设置时间序列
s=10*sin(0.4*pi*t);    % 原始信号
ns=randn(size(s));     % 产生噪声序列
y=s+ns;                % 构成带噪信号
x=sgolayfilt(y,3,19);  % 通过Savitzky-Golay滤波器
% 作图
figure
plot(t,y,'r'); 
xlim([0 20]); hold on; grid;
plot(t,x,'k');
xlabel('时间'); ylabel('幅值');
title('Savitzky-Golay滤波器的输/输出波形图')
set(gcf,'color','w');

获取代码请关注MATLAB科研小白的个人公众号（即文章下方二维码），并回复平滑处理本公众号致力于解决找代码难，写代码怵。各位有什么急需的代码，欢迎后台留言~不定时更新科研技巧类推文，可以一起探讨科研，写作，文献，代码等诸多学术问题，我们一起进步。