Analysis Steps of MRI data

1. the general procedure for fMRI analysis can be divided into the following three steps:

1. Preprocessing: Spatial and temporal preprocessing of the data to prepare it for the 1st and 2nd level inferential analysis
2. Model Specification and Estimation: Specifying and estimating parameters of the statistical model
3. Statistical Inference: Making inferences about the estimated parameters using appropriate statistical methods

     Step 1: Preprocessing

Slice Timing Correction (fMRI only)

        Because functional MRI measurement sequences don’t acquire every slice in a volume at the same time we have to account for the time differences among the slices.Slices are typically acquired in one of three methods: descending order (top-down); ascending order (bottom-up); or interleaved (acquire every other slice in each direction), where the interleaving may start at the top or the bottom. (Left:ascending, Right:interleaved).

        Slice Timing Correction is used to compensate for the time differences between the slice acquisitions by temporally interpolating the slices so that the resulting volume is close to equivalent to acquiring the whole brain image at a single time point. This temporal factor of acquisition especially has to be accounted for in fMRI models where timing is an important factor (e.g. for event related designs, where the type of stimulus changes from volume to volume).

Motion Correction (fMRI only)

        Motion correction, also known as Realignment, is used to correct for head movement during the acquisition of functional data. Even small head movements lead to unwanted variation in voxels and reduce the quality of your data. Motion correction tries to minimize the influence of movement on your data by aligning your data to a reference time volume. This reference time volume is usually the mean image of all timepoints, but it could also be the first, or some other, time point.

        Head movement can be characterized by six parameters: Three translation parameters which code movement in the directions of the three dimensional axes, movement along the X, Y, or Z axes; and three rotation parameters which code rotation about those axes, rotation centered on each of the X, Y, and Z axes).

        Realignment usually uses an affine rigid body transformation to manipulate the data in those six parameters. That is, each image can be moved but not distorted to best align with all the other images. Below you see a plot of a “good” subject where the movement is minimal.

Artifact Detection (fMRI only)

         Almost no subjects lie perfectly still. As we can see from the sharp spikes in the graphs below, some move quite drastically. Severe, sudden movement can contaminate your analysis quite severely.

          Motion correction tries to correct for smaller movements, but sometimes it’s best to just remove the images acquired during extreme rapid movement. We useArtifact Detection to identify the timepoints/images of the functional image that vary so much they should be excluded from further analysis and to label them so they are excluded from subsequent analyses.

          For example, checking the translation and rotation graphs for a session shown above for sudden movement greater than 2 standard deviations from the mean, or for movement greater than 1mm, artifact detection would show that images 16-19, 21, 22 and 169-172 should be excluded from further analysis. The graph produced by artifact detection, with vertical lines corresponding to images with drastic variation is shown below.

Coregistration

        Motion correction aligns all the images within a volume so they are ‘aligned’. Coregistration aligns the functional image with the reference structural image. If you think of the functional image as having been printed on tracing paper, coregistration moves that image around on the reference image until the alignment is at its best. In other words, coregistration tries to superimpose the functional image perfectly on the anatomical image. This allows further transformations of the anatomical image, such as normalization, to be directly applied to the functional image.

        The following picture shows an example of good (top) and bad (bottom) coregistration of functional images with the corresponding anatomical images. The red lines are the outline of the cortical folds of the anatomical image superimposed on the underlying greyscale functional image.

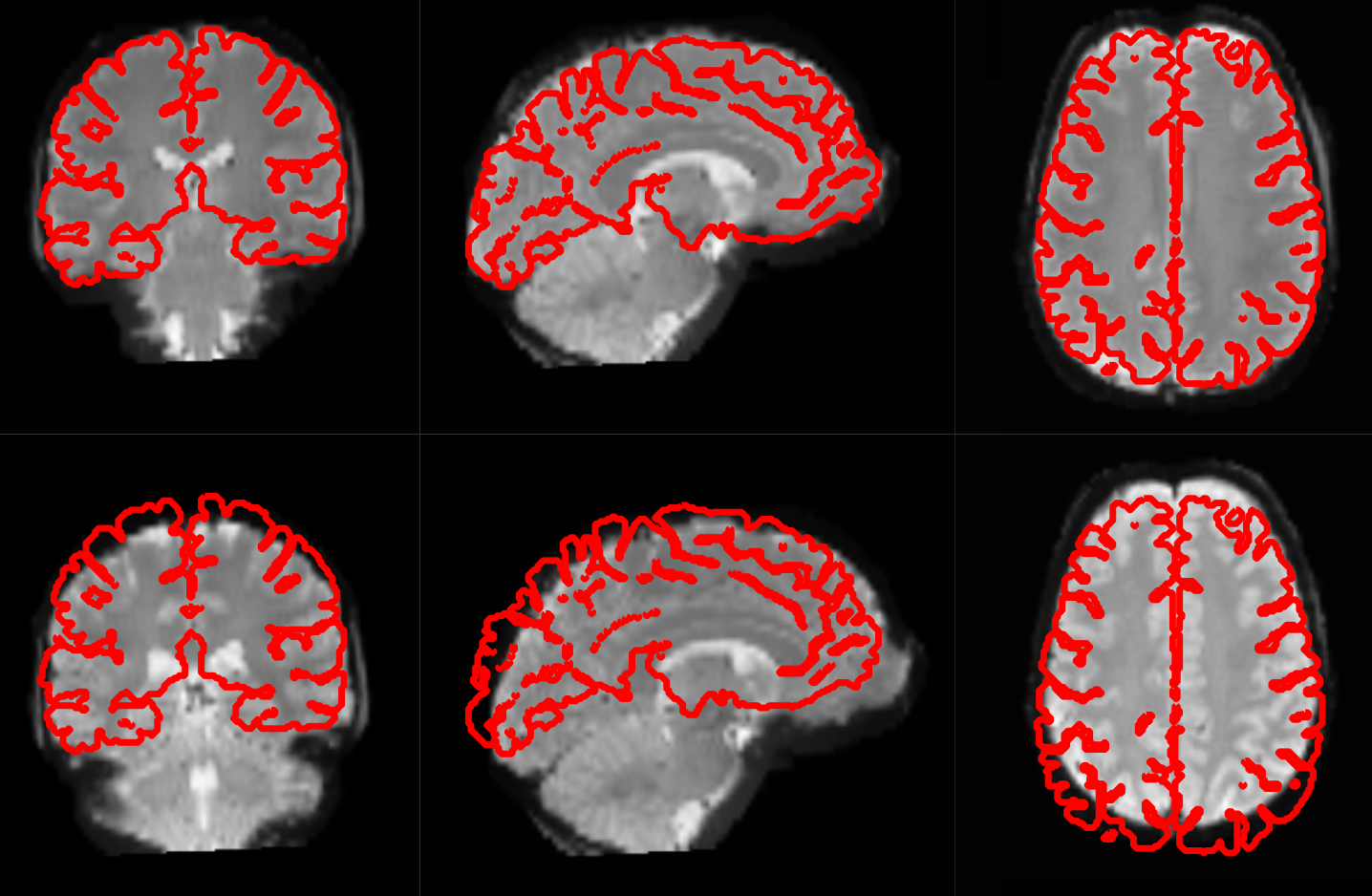
Normalization

          Every person’s brain is slightly different from every other’s. Brains differ in size and shape. To compare the images of one person’s brain to another’s, the images must first be translated onto a common shape and size, which is called normalization. Normalization maps data from the individual subject-space it was measured in onto a reference-space. Once this step is completed, a group analysis or comparison among data can be performed. There are different ways to normalize data but it always includes a template and a source image.

• The template image is the standard brain in reference-space onto which you want to map your data. This can be a Talairach-, MNI-, or SPM-template, or some other reference image you choose to use.
• The source image (normally a higher resolution structural image) is used to calculate the transformation matrix necessary to map the source image onto the template image. This transformation matrix is then used to map the rest of your images (functional and structural) into the reference-space.

Smoothing

         Structural as well as functional images are smoothed by applying a filter to the image. Smoothing increases the signal to noise ratio of your data by filtering the highest frequencies from the frequency domain; that is, removing the smallest scale changes among voxels. That helps to make the larger scale changes more apparent. There is some inherent variability in functional location among individuals, and smoothing helps to reduce spatial differences between subjects and therefore aids comparing multiple subjects. The trade-off, of course, is that you lose resolution by smoothing. Keep in mind, though, that smoothing can cause regions that are functionally different to combine with each other. In such cases a surface based analysis with smoothing on the surface might be a better choice.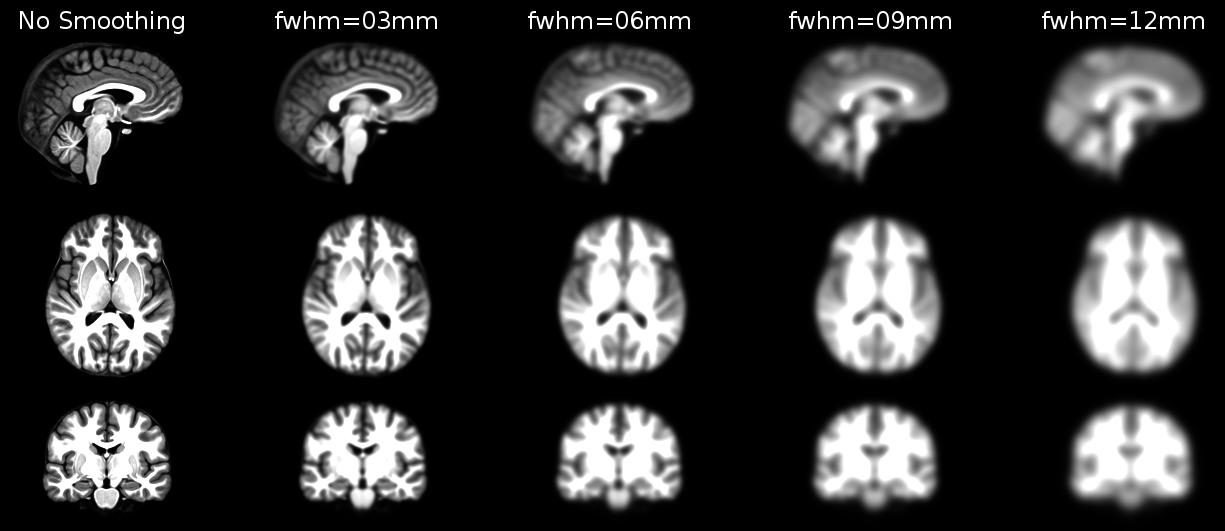

               Smoothing is implemented by applying a 3D Gaussian kernel to the image, and the amount of smoothing is typically determined by its full width at half maximum (FWHM) parameter. As the name implies, FWHM is the width/diameter of the smoothing kernel at half of its height. Each voxel’s value is changed to the result of applying this smoothing kernel to its original value.

               Choosing the size of the smoothing kernel also depends on your reason for smoothing. If you want to study a small region, a large kernel might smooth your data too much. The filter shouldn’t generally be larger than the activation you’re trying to detect. Thus, the amount of smoothing that you should use is determined partly by the question you want to answer. Some authors suggest using twice the voxel dimensions as a reasonable starting point.

Segmentation (sMRI only)

          Segmentation is the process by which a brain is divided into neurological sections according to a given template specification. This can be rather general, for example, segmenting the brain into gray matter, white matter and cerebrospinal fluid, as is done with SPM’s Segmentation, or quite detailed, segmenting into specific functional regions and their subregions, as is done with FreeSurfer’srecon-all, and that is illustrated in the figure.

          Segmentation can be used for different things. You can use the segmentation to aid the normalization process or use it to aid further analysis by using a specific segmentation as a mask or as the definition of a specific region of interest (ROI).

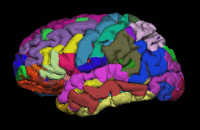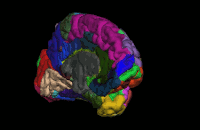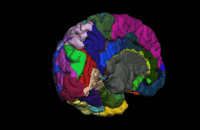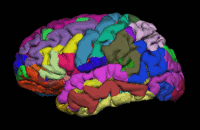
Step 2: Model Specification and Estimation

       To test our hypothesis on our data we first need to specify a model that incorporates this hypothesis and accounts for multiple factors such as the expected function of the BOLD signal, the movement during measurement, experiment specify parameters and other regressors and covariates. Such a model is usually represented by a Generalized Linear Model (GLM).

The General Linear Model

        A GLM describes a response (y), such as the BOLD response in a voxel, in terms of all its contributing factors (xβ) in a linear combination, whilst also accounting for the contribution of error (ε). The column (y) corresponds to one voxel and one row in this column corresponds to one time-point.

• y = dependent variable

  observed data (e.g. BOLD response in a single voxel)

• X = Independent Variable (aka. Predictor)

  e.g. experimental conditions (embodies all available knowledge about experimentally controlled factors and potential confounds), stimulus information (onset and duration of stimuli), expected shape of BOLD response

• β = Parameters (aka regression coefficient/beta weights)

  Quantifies how much each predictor ( X) independently influences the dependent variable ( Y)

• ε = Error

  Variance in the data ( Y) which is not explained by the linear combination of predictors ( Xβ). The error is assumed to be normally distributed.

          The predictor variables are stored in a so called Design Matrix. Theβ parameters define the contribution of each component of this design matrix to the model. They are estimated so as to minimize the error, and are used to generate thecontrasts between conditions. The Errors is the difference between the observed data and the model defined by Xβ.

Potential problems of the GLM approach

BOLD responses have a delayed and dispersed form

• We have to take the time delay and the HRF shape of the BOLD response into account when we create our design matrix.

BOLD signals include substantial amounts of low-frequency noise

• By high pass filtering our data and adding time regressors of 1st, 2nd,... order we can correct for low-frequency drifts in our measured data. This low frequency signals are caused by non-experimental effects, such as scanner drift etc.

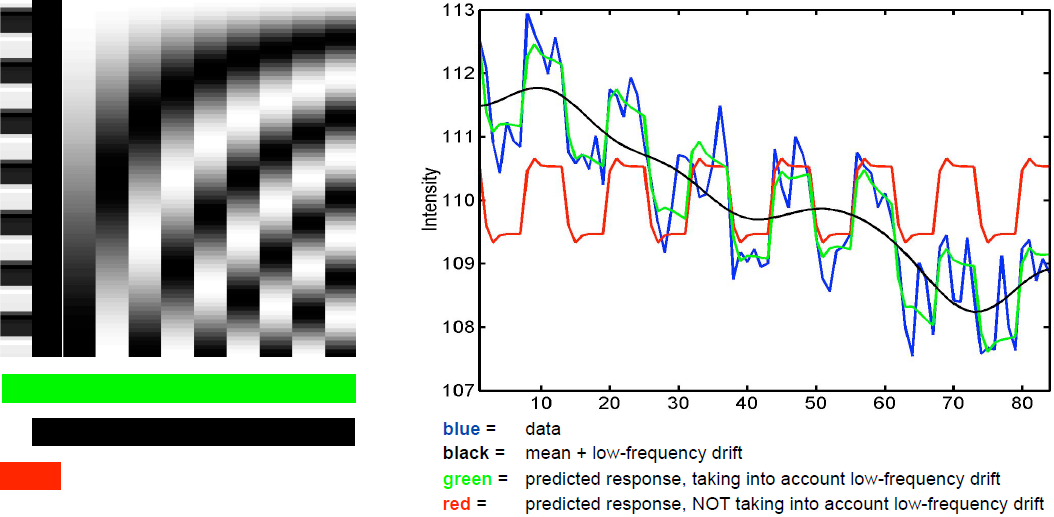
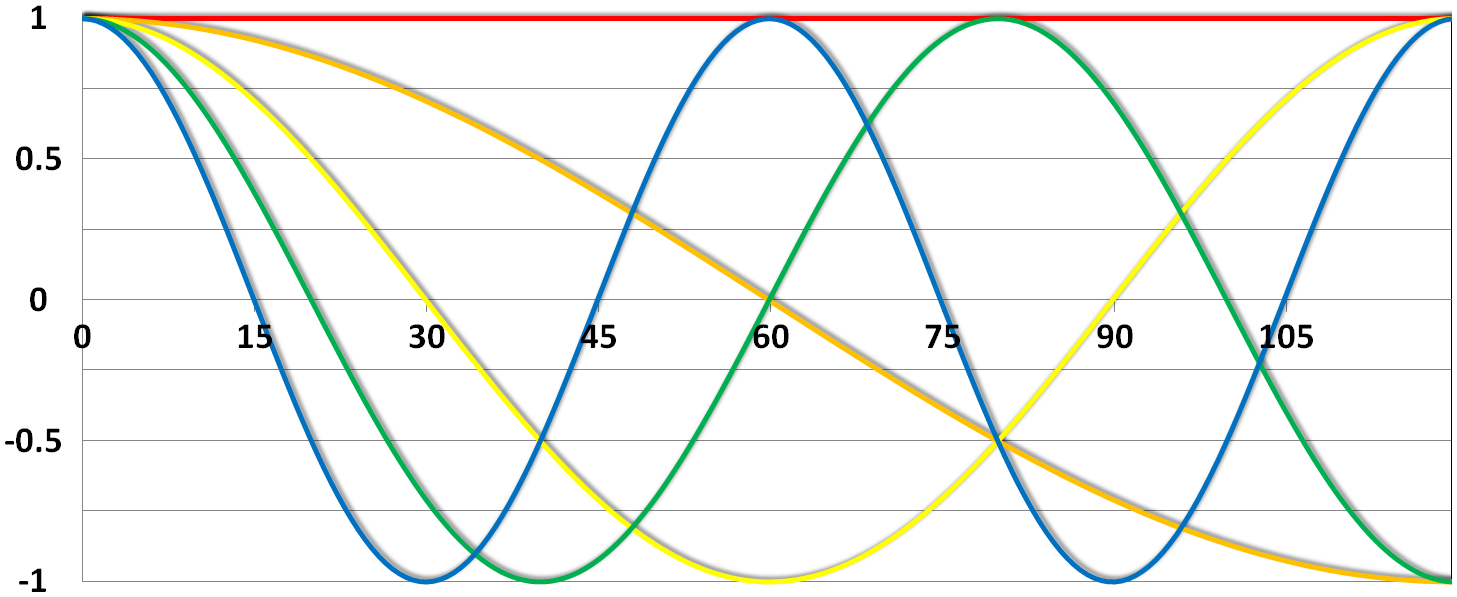
       This High pass Filter is established by setting up discrete cosine functions over the time period of your acquisition. In the example below you see a constant term of 1, followed by half of a cosine function increasing by half a period for each following curve. Such regressors correct for the influence of changes in the low-frequency spectrum.

Example of a Design Matrix

       Let us assume we have an experiment where we present subjects faces of humans and animals alike. Our goal is to measure the difference between the brain activation when a face of an animal is presented in contrast to the activation of the brain when a human face is presented. Our experiment is set up in such a way that subjects have two different blocks of stimuli presentation. In both blocks there are timepoints where faces of humans, faces of animals and no faces (resting state) are presented.

       Now, we combine all that we know about our model into one single Design Matrix. This Matrix contains multiple columns, which contain information about the stimuli (onset, duration and curve function of the BOLD-signal i.e. the shape of the HRF). In our example column Sn(1) humans and Sn(1) animals code for the stimuli of humans and animals during the first session of our fictive experiment. Accordingly, Sn(2) codes for all the regressors in the second session.Sn(1) resting codes for the timepoints where subjects weren’t presented any stimuli.

The y-axis codes for the measured scan or the passed time, depending on the specification of your design. The x-axis stands for all the regressors that we specified.

      The regressors Sn(1) R1 to Sn(1) R6 stand for the movement parameters we got from the realignment process. The regressorsSn(1) linear, Sn(1) quadratic, Sn(1) cubic and Sn(1) quartic are just examples of correction for the low frequency in your data. If you are using a high-pass filter of e.g. 128 seconds you don’t need to specifically include those regressors in your design matrix.

Note

Adding one more regressors to your model decrease the degrees of freedom in your statistical tests by one.

Model Estimation

       After we specified the parameters of our model in a design matrix we are ready to estimate our model. This means that we apply our model on the time course of each and every voxel.

       Depending on the software you are using you might get different types of results. If you are usingSPM the following images are created each time an analysis is performed (1st or 2nd level):

• beta images

  images of estimated regression coefficients (parameter estimate). beta images contain information about the size of the effect of interest. A given voxel in each beta image will have a value related to the size of effect for that explanatory variable.

• error image - ResMS-image

  residual sum of squares or variance image. It is a measure of within-subject error at the 1st level or between-subject error at the 2nd level analysis. This image is used to produce spmT images.

• con images - con-images

  during contrast estimation beta images are linearly combined to produce relevant con-images

• T images - spmT-images

  during contrast estimation the beta values of a con-image are combined with error values of the ResMS-image to calculate the t-value at each voxel

Step 3: Statistical Inference

Before we go into the specifics of a statistical analysis, let me explain you the difference between a 1st and a 2nd level analysis.

1st level analysis (within-subject)

A 1st level analysis is the statistical analysis done on each and every subject by itself. For this procedure the data doesn’t have to be normalized, i.e in a common reference space. A design matrix on this level controls for subject specific parameters as movement, respiration, heart beat, etc.

2nd level analysis (between-subject)

A 2nd level analysis is the statistical analysis done on the group. To be able to do this, our subject specific data has to be normalized and transformed from subject-space into reference-space. Otherwise we wouldn’t be able to compare subjects between each other. Additionally, all contrasts of the 1st level analysis have to be estimated because the model of the 2nd level analysis is conducted on them. The design matrix of the 2nd level analysis controls for subject specific parameters such as age, gender, socio-economic parameters, etc. At this point we also specify the group assignment of each subject.

Contrast Estimation

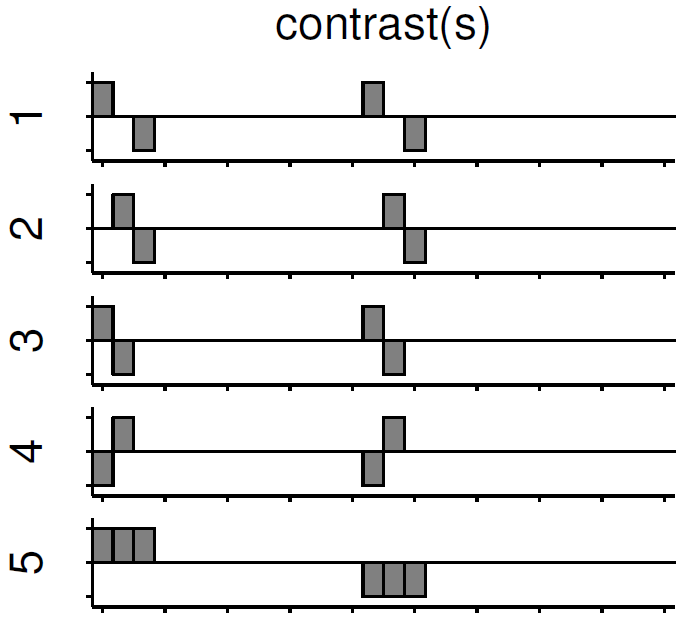
        Independent of the level of your analysis, after you’ve specified and estimated your model you now have to estimate the contrasts you are interested in. In such acontrast you specify how to weight the different regressors of your design matrix and combine them in one single image.

        For example, if you want to compare the brain activation during the presentation of human faces compared to the brain activation during the presentation of animal faces over two sessions you have to weight the regressorsSn(1) humans and Sn(2) humans with 1 and Sn(1) animals andSn(2) animals with -1, as can be seen in contrast 3. This will subtract the value of the animal-activation from the activation during the presentation of human faces. The result is an image where the positive activation stands for “more active” during the presentation of human faces than during the presentation of animal faces.

         Contrast 1 codes for human faces vs. resting, contrast 2 codes foranimal faces vs. resting, contrast 4 codes for animal faces vs. human faces (which is just the inverse image of contrast 3) and contrast 5 codes forsession 1 vs. session 2, which looks for regions which were more active in the first session than in the second session.

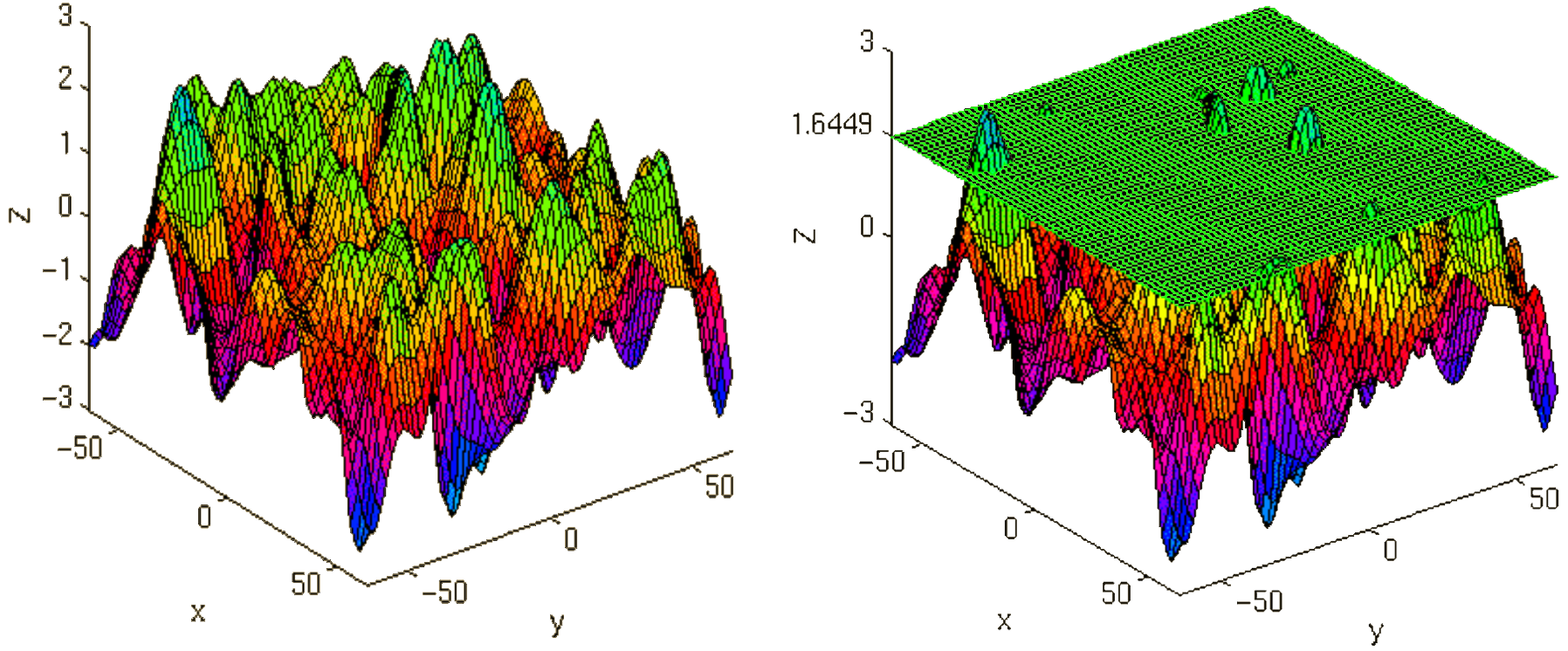
Thresholding

         After the contrasts are estimated there is only one final step to be taken before you get a scientific based answer to your question. You have to threshold your results. With that I mean, you have to specify the level of significance you want to test your data on, you have to correct for multiple comparison and you have to specify the parameters of the results you are looking for. E.g.:

• FWE-correction: The family-wise error correction is one way to correct for multiple comparisons
• p-value: specify the hight of the significance threshold that you want to use (e.g. z=1.6449 equals p<0.05 (one-tailed); see image)
• voxel extend: specify the minimum size of a “significant” cluster by specifying the number of voxel it at least has to contain.

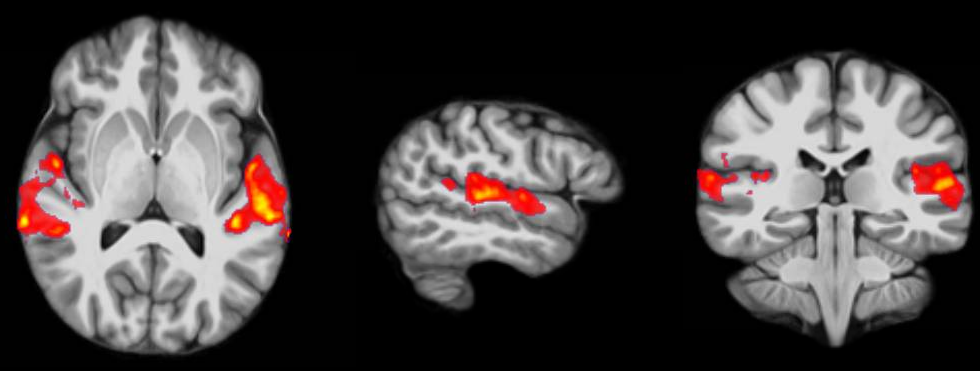
        If you do all this correctly, you’ll end up with something as shown in the following picture. The picture shows you the average brain activation of 20 subjects during the presentation of an acoustic stimuli. The p-value are shown from red to yellow, representing values from 0.05 to 0.00. Shown are only cluster with a voxel extend of at least 100 voxels.