Pipage Rounding 学习笔记

Pipage Rounding 学习笔记

Author: Sijin Yu

本文基本只作简单的翻译工作. 未经作者授权不得转载.

1. Linear Programming (线性规划)

线性规划可以表示为

$$\begin{array}{rl}\min & c\cdot x\\ \text{subject to }& Ax\ge b\end{array}$$

其中, $n$ 为变量个数 ($x$ 的维度), $m$ 为非平凡约束的个数.
则:

• $A$ 有 $(m+n)$ 行和 $n$ 列, 且 $\text{rank}(A)=n$.
• 令 $Bx=b_B$, 其中 $\text{rank}(B)=n$, $B$ 是 $A$ 的子阵, $b_B$ 是 $b$ 中对应的元素.

1.1 基本定义

$$\begin{array}{rl}\min & c\cdot x\\ \text{subject to }& Ax\ge b\end{array}$$

• 基: $A$ 中 $n$ 列向量组成的线性无关的可逆矩阵 (就是 $B$).

• 基向量: 基 $B$ 中任意一个列向量.

• 基本解: $Bx=b_B$ 的解.

• 可行解: 在多面体 $Ax\ge b$ 中的解.

• 基本可行解: 同时是基本解和可行解的解.

1.2 基本定理

• 对每个 LP 问题, 都存在一个最优解是基本可行解.

设 $x$ 为一个基本可行解, 令 supp ( x ) : = { i : x i > 0 } \text{supp}(x):=\{i:x_i>0\} supp(x):={i:xi​>0}.

• 对每个 LP 问题, 都存在一个最优解, 使至少 $\text{supp}(x)$ 个线性无关的的非平凡约束取等号.

定理: 对于一个凸集 $k$ 与凸集外一点 $x$, 总存在超平面使得 $k$ 与 $x$ 分居两侧.

Separation Oracle: 给定一个点 $x$, 其关于凸集合 $k$ 的 separation oracle 为: 要么说明 $x\in k$, 要么返回一个分割 $x$ 与 $k$ 的超平面.

• 如果 $m=\text{ploy(n)}$, 则存在多项式时间的 Separation Oracle 算法.

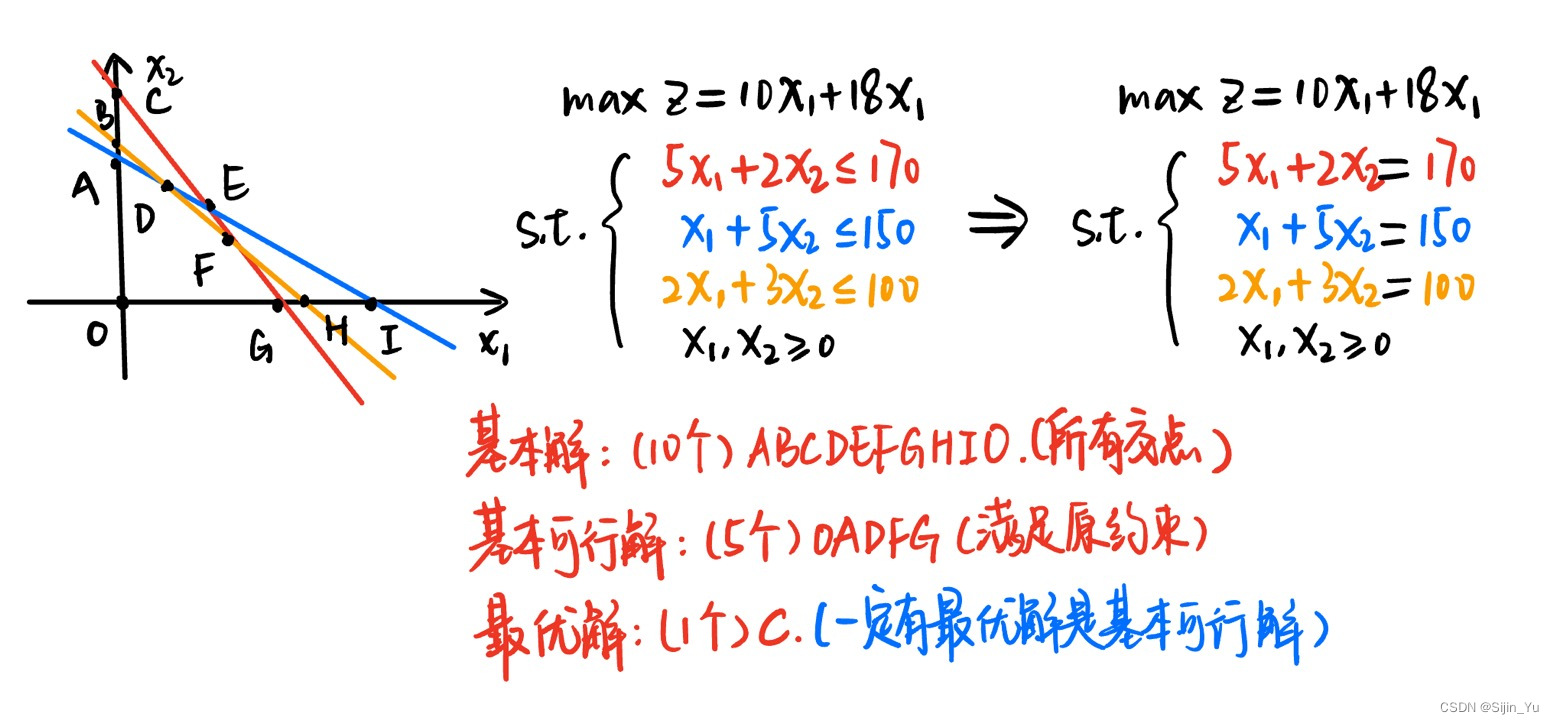
该图直观解释了: 总存在一个最优解是基本可行解.

1.3 椭球算法

椭球算法是一个在多项式时间内解决线性规划问题的算法.

算法步骤:

Step 1 猜想一个可能的 $M$, 判断 $c\cdot x\le M$ 和约束 $Ax\ge b$ 是否满足.

• 若满足: 降低 $M$ 值, 重新执行 Step 1.
• 若不满足: 得到分割超平面, 并提高 $M$ 至超平面另一侧.

经过有限次迭代, $M$ 趋于取最优解时 $c\cdot x$ 的值.

Step 1 的判断本质上是将 $c\cdot x\le M$ 放入约束中, 并针对 $x$ 和新约束对应的多面体执行 Separation Oracle 算法.

总结 of 1. Linear Programming (线性规划)

• 线性规划为: 在一个超多面体内寻找一个点, 使一个线性的函数取得最小值.
• 总存在一个最优解, 是基本可行解.
• 一个最优的基本可行解可在多项式时间内被找到.

---

2. Pipage Rounding

背景:

当线性规划的解只能取整数解时, 即原 LP 问题变为:
$$\begin{array}{rl}\min & c\cdot x\\ \text{subject to }& Ax\ge b\\ & x_j\in \mathbb{N},\forall j\in [n]\end{array}$$
则, 从线性规划变为整数规划, 问题从多项式变为 NP-hard.

2.1 Linear Relaxations (线性松弛)

现在考虑 0-1 规划问题, 即 x j ∈ { 0 , 1 } , ∀ j ∈ [ n ] x_j \in \{0,1\}, \forall j\in[n] xj​∈{0,1},∀j∈[n].

线性松弛: 将整数约束 x j ∈ { 0 , 1 } x_j \in \{0,1\} xj​∈{0,1} 用分数约束 $0\le x_j\le 1$ 替代, 在多项式时间内可解得分数约束下的最优解. 然后使用 pipage rounding 将分数下的最优解 “round” 到整数下, 可以证明这样的解是一个近似最优.

2.2 Pipage Rounding

记 $\mathcal{P}$ 为一 $n$ 维多面体. 一个 0-1 规划问题为:
max ⁡ { F ( x ) :     x ∈ P ∩ { 0 , 1 } n } \max\{F(x): ~~~x\in\mathcal{P}\cap\{0,1\}^n\} max{F(x):   x∈P∩{0,1}n}
其中, $F(x)$ 为目标函数, $\mathcal{P}$ 为约束条件.

假设:

1. 对所有非整数的 $x\in \mathcal{P}$, 总是存在一个向量 $v_x$ 与两个标量 ${\alpha }_x,{\beta }_x>0$, 使得:
   $x+{\alpha }_x{v}_x$ 与 $x-{\beta }_x{v}_x$ 比起 $x$ 都有严格更大数量的整数坐标.
2. $F(x)$ 在 $v_x$ 方向上是凸函数.

则, 存在 pipage rounding 的方法,使: 给定任意的分数向量 $x\in \mathcal{P}$, 总能找到整数向量 $x^{\text{int}}\in \mathcal{P}$, 使得 $F(x^{\text{int}})\ge F(x)$ 成立.

Pipage Rounding 的一个例子

• 记 P : = { x ∈ [ 0 , 1 ] n : ∑ j = 1 n x j = k } \mathcal P:=\{x\in[0,1]^n: \sum_{j=1}^n x_j=k\} P:={x∈[0,1]n:∑j=1n​xj​=k}.

• 假设 $x$ 是 $\mathcal{P}$ 中的非整数向量, 则至少存在两个分数坐标, 记为 $x_p$ 和 $x_q$.

• 令 $e_p$ 和 $e_q$ 为 $x_p$ 和 $x_q$ 分量方向上的单位向量. 即 $e_p$ 在第 $p$ 个坐标为 $1$, 其它坐标为 $0$, $e_q$ 同理.

• 令 $v_x=e_p-e_q$, 令 ${\alpha }_x=\min (1-x_p,x_q)$, 令 ${\beta }_x=\min (1-x_q,x_p)$.

则 $x+{\alpha }_x{v}_x$ 和 $x-{\beta }_x{v}_x$ 总是能在第 $p$ 和 $q$ 分量上取整数, 且由于 $F(x)$ 在 $v_x$ 是凸的, 则必有 $F(x+{\alpha }_x{v}_x)\ge F(x)$ 和 $F(x-{\beta }_x{v}_x)\ge F(x)$ 成立.

满足上假设时, 存在 Pipage Rounding 的算法, 将一个线性规划的最优解转化为整数规划的近似最优解 (在 Pipage Rouning 下整数规划也是最优解).

若 Pipage Rounding 是可应用的, 必然存在: $\mathcal{P}$ 是整数的多面体.

2.3 在拟阵约束下最大化单调次模函数

定义

对于集函数 $f:2^U\to {\mathbb{Z}}_{\ge 0}$ 而言:

• 次模 (submodular): (子模) $f$ 是次模的, 若 $\forall A,B\subseteq U$, 总有 $f(A)+f(B)\ge f(A\cup B)+f(A\cap B)$.

• 单调 (monotone): $f$ 是单调的, 若 $\forall A\subseteq B$, 总有 $f(A)\le f(B)$.

定义

• 拟阵 (matroid): $M:=(U,\mathcal{I})$ 为拟阵, 若其满足:
  1. 若 $B\in \mathcal{I}$ 且 $A\subseteq B$, 则 $A\in \mathcal{I}$,
  2. $\forall A,B\in \mathcal{I},|A|<|B|$ 总存在一个 $i\in B$ 使得 A ∪ { i } ∈ I A \cup \{i\}\in \mathcal I A∪{i}∈I.

$\mathcal{I}$ 被称为独立集 (independent sets).

• 基 (base): $T$ 是拟阵 $M$ 的基, 若 $T\in \mathcal{I}$ 且 $\mathcal{I}$ 中没有势大于 $|T|$ 的独立集.

• 凸包 (convex hull): 给定一个集合 $X$, 所有包含 $X$ 的凸集的交集 $S$ 称为 $X$ 的凸包.

$X$ 的凸包可以用 $X$ 内所有点的凸组合来构造. 在二维欧式空间中, 一些点的凸包可以想象为将它们刚好包围起来的多边形(顶点为这些点构成)的内部所有点.

定义

• 特征向量 (characteristic vector): 给定一个集合 $S\in \mathcal{I}$, $S$ 的特征向量为一个 { 0 , 1 } n \{0,1\}^n {0,1}n 内的向量, 其第 $i$ 个分量为 $1$ 若 $i\in S$.

• 秩 (rank): 给定一个集合 $S\subseteq U$, $S$ 的秩 $r_M(S)$ 为 $S$ 的最大独立子集的势.

• 拟阵多面体 (matroid polytope): 拟阵多面体 $\mathcal{P}$ 被定义为:

  P : = { x ∈ [ 0 , 1 ] n :     ∑ i ∈ S x i ≤ r M ( S ) , ∀ S ⊆ [ n ] } . \mathcal P:=\{x\in[0,1]^n:~~~\sum_{i\in S}x_i\leq r_M(S),\forall S\subseteq[n]\}. P:={x∈[0,1]n:   i∈S∑​xi​≤rM​(S),∀S⊆[n]}.

最大生成树

可被抽象为最大生成树问题的拟阵为可图拟阵 (graphic matroid).

令 $G=(V,E)$ 为简单图, 拟阵 $M:=(E,\mathcal{I})$, 其中 $\mathcal{I}$ 为 $G$ 的全体无圈子图. 拟阵 $M$ 的一个基 $T$ 表示图 $G$ 的一个最大生成树. 其中次模函数 $f$ 为 $f(S)=|S|$. 给定一个边集 $S\subseteq E$, $S$ 的秩 $r_M(S)$ 为 $S$ 中最大无圈子图的边数.

则拟阵多面体为 P : = { x ∈ [ 0 , 1 ] ∣ E ∣ :     ∑ i ∈ S x i ≤ r M ( S ) , ∀ S ⊆ 2 E } \mathcal P:=\{x\in[0,1]^{|E|}:~~~\sum_{i\in S}x_i\leq r_M(S),\forall S\subseteq 2^E\} P:={x∈[0,1]∣E∣:   ∑i∈S​xi​≤rM​(S),∀S⊆2E}.

目标函数为 $\max f(x)={\sum }_i{x}_i$.

次模函数到连续非线性函数

给定次模函数 $f$, 定义 $F:[0,1{]}^n\to {\mathbb{R}}_{\ge 0}$ 如下:
$$F(x_1,...,x_n):=\sum _{S\subseteq [n]}\left(f(S)\prod _{i\in S}{x}_i\prod _{i\notin S}(1-x_i)\right)$$
且:

• $f$ 是单调的, 因此 $\frac{\partial F}{\partial x_i}\ge 0,\forall i,\forall x$.
• $f$ 是次模的, 因此 $\frac{{\partial }^{2}F}{\partial x_i\partial x_j}\ge 0,\forall i\ne j,\forall x$.

$F(x_1,...,x_n)$ 可以看作是 $f(S)$ 的期望值, 其中 $S$ 由对各元素 $i$ 以独立的概率 $x_i$ 采样获得.

若 $F(x_1,...,x_n)$ 满足上述要求, 且 $\nabla F$ 可知, 则有:

若给定向量 $v\in \mathcal{P}$ 与各分量权重 $w_j$, $\max {\sum }_j{w}_j{v}_j$ 可在多项式时间内被找到, 则对于优化问题 $\max F(x):x\in \mathcal{P}$, 存在一个随机的 $1-\frac{1}{e}$ 近似算法.

---

3. Matching (匹配)

匹配

一个图 $G=(V,E)$ 的匹配 (matching) 是一个边的集合, 其中任意两条边没有公共顶点.

整数匹配问题 (Integral Matching Problem)

令 $f(e)=1$, 若 $e$ 在匹配中; 否则 $f(e)=0$.

整数匹配问题目标函数是 $\max {\sum }_{e\in E}f(e)$.

约束条件是 ∀ v ∈ V , ∑ e ∋ v f ( e ) ≤ 1 , f ( e ) ∈ { 0 , 1 } \forall v\in V,\sum_{e\ni v}f(e)\leq 1, f(e)\in\{0,1\} ∀v∈V,∑e∋v​f(e)≤1,f(e)∈{0,1}.

整数匹配的多项式时间求解

匈牙利算法可在多项式时间内求解整数匹配问题.

3.1 分数匹配

在分数匹配中, 将整数匹配的 f ( e ) ∈ { 0 , 1 } f(e)\in\{0,1\} f(e)∈{0,1} 整数限制改为分数限制 $f(e)\in [0,1]$.

分数匹配问题 (Fractional Matching Problem)

给定一个图 $G=(V,E)$, 分数函数 $f:E\to [0,1]$, 且对于每个 $v\in V$, 以 $v$ 为顶点的各边分数之和至多为 $1$.

分数匹配的目标函数是 $\max {\sum }_{e\in E}f(e)$.

约束条件是 $\forall v\in V,{\sum }_{e\ni v}f(e)\le 1,f(e)\in [0,1]$.

• 分数匹配是 NP-hard 问题.

3.2 Pipage Rounding Method

令 $x(e)=f(e)$, 拟阵多面体为 P : = { x ∈ [ 0 , 1 ] ∣ E ∣ :     ∑ e ∋ v x ( e ) ≤ 1 , ∀ v ∈ V , ∀ e ∈ E } \mathcal P:=\{x\in[0,1]^{|E|}:~~~\sum_{e\ni v}x(e)\leq1,\forall v\in V,\forall e\in E\} P:={x∈[0,1]∣E∣:   ∑e∋v​x(e)≤1,∀v∈V,∀e∈E}. 拟阵的一个基为 $T$.

目标: 给定一个分数点 $x$, 将其 round 到一个基 $T$ 上.

定义

tight: 一个集合 $S\subseteq E$ 关于分数点 $x$ 是 tight 的, 若 $x(S)=r_M(S)$.

定理

若两个有交集的集合 $S,T\subseteq E$ 关于 $x$ 都是 tight 的, 则 $S\cap T,S\cup T$ 都是 tight 的.

Pipage Rounding 算法

Step 1: 给定非整数点 $x$, 选择一个尽量小的 tight 的集合 $T$. 注意, $x$ 至少有两个非整数点 $0<x(e)<1,0<x(f)<1$.

Step 2: 过点 $x$ 画一条直线, 记往 $x(e)$ 递增方向为 $+1$, 往 $x(f)$ 递增方向为 $-1$. 保持 $x(e)+x(f)$ 不变, 随机地在该直线上移动, 直到碰到多面体的表面.

记 $x_1$ 和 $x_2$ 分别为直线在 $+1$ 和 $-1$ 方向上与拟阵多面体的交点, 我们以概率 $p$ 从 $x$ 到达 $x_1$, 以概率 $1-p$ 从 $x$ 到达 $x_2$. $p$ 取 $p{x}_1+(1-p)x_2=x$ 的解.

这一做法得到得到一个 tight 的集合 $S$.

Step 3: 令 $x\leftarrow x_1$ (或 $x_2$), $T\leftarrow S\cap T$, 重复 Step 1, 直到 $x$ 为整数点.

算法至多需要 $|E|\cdot r_M(E)$ 次迭代.

Pipage Rounding 算法的性质

1. 对于任意一个元素 $e$, $\mathbb{P}[e\in T]=x(e)$.
2. 元素之间是负相关的, 即

$$\mathbb{P}[S\subseteq T]\le \prod _{e\in T}x(e).$$

3.3 二部图

一个二部图的最小代价完美匹配问题 (min-cost perfect matching problem) 描述如下:

给定一个二部图 $G=(A,B,E)$,
$$\begin{array}{rlrl}\min & \sum _{e\in E}{c}_e{x}_e& & \\ \text{subject to }& x(\delta (a))=1& & \forall a\in A\\ & x(\delta (b))=1& & \forall b\in B\\ & 0\le x_e\le 1& & \forall e\in E\end{array}$$

令 $x^{\ast }$ 是一个最优解 (松弛情况).

定理: 对于任意一个 $x^{\ast }$, 存在一个边 $e$, 使 $x_e^{\ast }=0$ 或 $x_e^{\ast }=1$.

使用反证法, 若对所有 $e\in E$ 都有 $0<x_e<1$, 因为每个点分数之和为 $1$, 则必然每个点都至少连有两条边. 令 $|A|=|B|=n$, 有 $|E|>2n$. 则必须有 $2n$ 个线性无关的约束. 然而这些约束并不是线性独立的: 与 $A$ 相关的行之和与与 $B$ 相关的行之和相等.

Rounding: 如果 $x_e^{\ast }=0$, 我们删除 $e$. 如果 $x_e^{\ast }=1$, 我们把这条边放入 matching 里, 并移除这条边的两个端点. 然后, 我们得到了全新的 min-cost perfect matching 问题, 应用同样的方法, 直到得到整数解为止.

对二部图 matching 的 另一种 rounding:

记 $F\subseteq E$ 为分数边集合. 若 $F=\varnothing$, 则完成. 否则, 在子图 $(A,B,F)$ 中找到 (在线性时间内) 极大路径 $P$. 并将边集 $P$ 分为两个匹配 $M_1$ 和 $M_2$. 并且定义:
α = min ⁡ { γ > 0 : ( ( ∃ e ∈ M 1 : x e + γ = 1 ) ∨ ( ∃ e ∈ M 2 : x e − γ = 0 ) ) ; } β = min ⁡ { γ > 0 : ( ( ∃ e ∈ M 1 : x e − γ = 1 ) ∨ ( ∃ e ∈ M 2 : x e + γ = 0 ) ) ; } \begin{align*} \alpha=\min\{ \gamma>0:((\exists e\in M_1:x_e+\gamma=1 )\vee(\exists e\in M_2:x_e-\gamma=0)); \}\\ \beta =\min\{ \gamma>0:((\exists e\in M_1:x_e-\gamma=1 )\vee(\exists e\in M_2:x_e+\gamma=0));\} \end{align*} α=min{γ>0:((∃e∈M1​:xe​+γ=1)∨(∃e∈M2​:xe​−γ=0));}β=min{γ>0:((∃e∈M1​:xe​−γ=1)∨(∃e∈M2​:xe​+γ=0));}​

以概率 $\frac{\alpha }{\alpha +\beta }$, 对于所有 $e\in M_1$, 置 $x_e:=x_e+\alpha$; 对所有 $e\in M_2$, 置 $x_e:=x_e-\alpha$.

以概率 $\frac{\beta }{\alpha +\beta }$, 对于所有 $e\in M_1$, 置 $x_e:=x_e-\beta$; 对所有 $e\in M_2$, 置 $x_e:=x_e+\beta$.

对新获得的图, 执行一样的算法, 直到获得整数解.

Reference

[1] Lecture Notes, CSE 599: Recent Developments in Approximation Algorithms.
[2] Lecture Notes, CIS800: Techniques in Approximation Algorithms, Fall 2010.
[3] Gandhi R, Khuller S, Parthasarathy S, et al. Dependent rounding in bipartite graphs[C]//The 43rd Annual IEEE Symposium on Foundations of Computer Science, 2002. Proceedings. IEEE, 2002: 323-332.