Scheduling

最新推荐文章于 2022-02-23 23:22:23 发布

Akimoto Akira

最新推荐文章于 2022-02-23 23:22:23 发布

阅读量2k

点赞数 2

分类专栏： Synthesis and Optimization

本文链接：https://blog.csdn.net/zch951127/article/details/114909122

版权

Synthesis and Optimization 专栏收录该内容

8 篇文章

订阅专栏

这一节中将要介绍的是集成电路优化中的Scheduling。这一部分主要的工作是安排灭一部操作的顺序，使得其可以充分利用时间和芯片上的资源。为了更直观地表达，这里选用的model是Sequencing DFG.
在scheduling的过程中，在实际应用中会有各种各样的限制，主要的限制有时间，片上资源，area等。基本的Scheduling算法有ASAP和ALAP。其算法如下Fig1中伪代码所示。
ASAP
ALAP
Fig1 ASAP and ALAP
ASAP的主要思想是先将启示的节点固定，然后在下一个时钟周期内安排上所有其processor已经安排完毕的节点或是没有processor，一直循环到全部安排完毕。ALAP的主要思路是固定好最后一个终止点，这个终止点的固定可以使用ASAP算法先计算一次得出，或者根据限制条件得出。随后向起始点方向安排successor已经安排的节点或是没有successor的节点。这两种算法是最基本最简单的算法。
那么当我们的设计需求中有限制的情况下该怎么办呢？这里我以限制条件不同将其分成三种不同的情况进行介绍。

时间条件限制

这种限制主要出现的场景是在某些接口协议设计上。比如说要设计一个满足CAN总线协议的收发驱动芯片，其发送信号的终止时间和开始时间都要符合协议本身的内容。这种时间维度上的限制在设计中也分为好几种：

add forward edges for minimum constrains (i.e 下一个节点开始的时间必须晚于某一个时间)
add backward edges for maximum constrains (i.e 前一个节点的完成时间不得多于某一个节点的开始时间)

Fig 2中即为前两点的实际例子，假设ALU执行需要1个单位的延迟，乘法操作需要两个单位延迟。左边的图表示了两个不同的时间延迟限制条件

节点1到2最迟是3个Delay unit，即2节点的操作必须在3个延迟时间单位内开始
初始节点0到4的最小延迟为4，即4节点的开始时间必须相对0节点晚4个时间单位

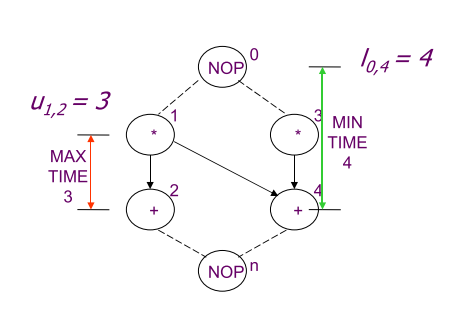
Fig2 示例前两个时间限制
对此，由于在图示中edge代表的是延迟的时间所以要schedule优化则需要对Edge进行权重的赋值来适应这些条件即我们可以得到schedule之后的Sequencing DFG，这个权重的赋值表示的时间是包括了操作占用的时间的，节点本身只代表了操作开始当时的时间如，Fig3所示。

Fig3 优化后的Sequencing DFG
显然1到2的时间间隔是小于3的这边是可取的，而0到4的间隔时间为2<4所以这边是不可取的。

资源限制

在一个硬件设计中用于操作的硬件资源是有限的，因此在这种情况下，当某些硬件资源被占用时另一些需要这些资源的操作就必须要等待或者寻找是否有可以替代的资源。在很多设计中，会有很多ALU或者乘法器之类的资源，根据实际操作的需要配置在芯片上。以提高操作的并行性能。这个问题在下一章中还会讲到。在本章中即采取stall的方式避免冲突。

同时存在资源和时间限制的调度问题

对于这个问题我们可以使用ILP的方式进行表达，表达之后可以使用标准ILP库(GNU Linear Programming Kit)解出来得到满足条件的scheduling。

每一个operation的开始时间（未知数）
$t_{i}=\sum_{l}l\cdot x_{i,l}$
其中的x_il是当有操作时赋值为1的矩阵。当所有l上的x_i都加起来的时候总和一定为1。这是为了限制一个操作仅仅会出现一次。具体出现在哪一行是不知道的。这里面的l是ASAP或者用限制条件计算出来的
操作的先后顺序条件（时间限制条件也可以放在这里）
$t_{i}\geqslant t_{j}+d_{j}$
资源限制条件
$\sum _{i:T(v_{i})=k} x_{i,j}\leqslant a_{k}$

除此之外，也可以写程序使用算法来解决问题。主要的使用的有两种：Hu’s algorithm和List scheduling algorithm
对于Hu’s algorithm其伪代码如图Fig4所示。这个对于nodes的编号一般是使用相对终止节点的时间长短来编号，这个编号会影响到获取资源的优先级。而且这个算法是有一定限制条件的：

所有的操作有相同的延迟时间
所有的操作用的都是同一个resource

Fig4 Hu’s algorithm
而List scheduling algorithms没有这样的限制可以应用于更多场合。如图Fig5所示。这个算法是用于减少延迟时间的算法，如果需要找到同时使用资源的最小个数需要使用Fig6中的算法。

Fig5 List Scheduling Algorithm for min-latency

Fig6 List Scheduling Algorithm for min-resource