Opencv2.4.9源码分析——phaseCorrelate

相位相关法（phase correlate）可以用于检测两幅内容相同的图像之间的相对位移量。它是基于傅立叶变换的位移定理：一个平移过的函数的傅立叶变换仅仅是未平移函数的傅立叶变换与一个具有线性相位的指数因子的乘积，即空间域中的平移会造成频域中频谱的相移。它的公式定义为：设二维函数（图像）f(x,y)的傅立叶变换为F(u,v)，即DFT[f(x,y)]=F(u,v)，如果f(x,y)平移(a,b)，则平移后的傅立叶变换为：

        （1）

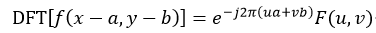
因此，当两幅函数f₁(x,y)和f₂(x,y)仅仅有位移的差异，即f₂(x,y)= f₁(x-a,y-b)，则它们的傅立叶变换F₁(u,v)和F₂(u,v)有如下关系：

         （2）

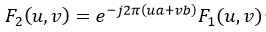
由上式很容易得到f₁(x,y)和f₂(x,y)的互功率谱为（这里还用到了f₁(x,y)和f₂(x,y)的频谱的模相等）：

         （3）

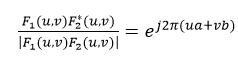
式中F^*表示F的共轭，上式表示平移定理保证了互功率谱的相位等于两幅图像之间的相移。

Opencv的文档给出了详细的用相位相关法求解位移量的过程，

1、对待处理的两幅图像src1和src2应用窗函数去除图像的边界效应，文档中推荐使用汉宁窗，它可用createHanningWindow函数生成；

2、求傅立叶变换：G_a