转自:http://blog.csdn.net/u012162613/article/details/45920827
1.流形学习的概念
流形学习方法(Manifold Learning),简称流形学习,自2000年在著名的科学杂志《Science》被首次提出以来,已成为信息科学领域的研究热点。在理论和应用上,流形学习方法都具有重要的研究意义。
假设数据是均匀采样于一个高维欧氏空间中的低维流形,流形学习就是从高维采样数据中恢复低维流形结构,即找到高维空间中的低维流形,并求出相应的嵌入映射,以实现维数约简或者数据可视化。它是从观测到的现象中去寻找事物的本质,找到产生数据的内在规律。
以上选自百度百科
简单地理解,流形学习方法可以用来对高维数据降维,如果将维度降到2维或3维,我们就能将原始数据可视化,从而对数据的分布有直观的了解,发现一些可能存在的规律。
"
官方代码思想是一遍聚类一遍降维,其实也是一种比较好的自动聚类方法。
高维数据每个数据点被认为是一种正太分布数据(正太有三好),低维数据同样,然后让高维数据和低维数据相似度最大。又因为t分布好算而且和正太分布逼近,所以用了t分布来算就成了tsne方法。
"
2.流形学习的分类
可以将流形学习方法分为线性的和非线性的两种,线性的流形学习方法如我们熟知的主成份分析(PCA),非线性的流形学习方法如等距映射(Isomap)、拉普拉斯特征映射(Laplacian eigenmaps,LE)、局部线性嵌入(Locally-linear embedding,LLE)。
当然,流形学习方法不止这些,因学识尚浅,在此我就不展开了,对于它们的原理,也不是一篇文章就能说明白的。对各种流形学习方法的介绍,网上有一篇不错的读物(原作已找不到): 流形学习 (Manifold Learning)
3.高维数据降维与可视化
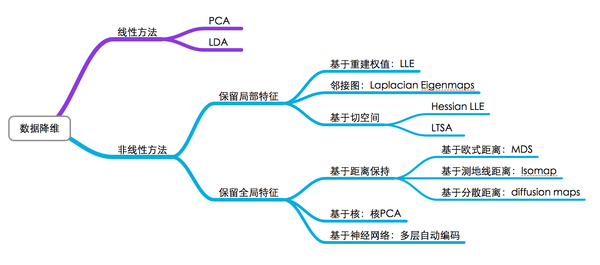
对于数据降维,有一张图片总结得很好(同样,我不知道原始出处):
图中基本上包括了大多数流形学习方法,不过这里面没有t-SNE,相比于其他算法,t-SNE算是比较新的一种方法,也是效果比较好的一种方法。t-SNE是深度学习大牛Hinton和lvdmaaten(他的弟子?)在2008年提出的,lvdmaaten对t-SNE有个主页介绍:tsne,包括论文以及各种编程语言的实现。
接下来是一个小实验,对MNIST数据集降维和可视化,采用了十多种算法,算法在sklearn里都已集成,画图工具采用matplotlib。大部分实验内容都是参考sklearn这里的example,稍微做了些修改。
Matlab用户可以使用lvdmaaten提供的工具箱: drtoolbox
- 加载数据
MNIST数据从sklearn集成的datasets模块获取,代码如下,为了后面观察起来更明显,我这里只选取n_class=5,也就是0~4这5种digits。每张图片的大小是8*8,展开后就是64维。
digits = datasets.load_digits(n_class=5) X = digits.data y = digits.target printX.shape n_img_per_row = 20 img = np.zeros((10 * n_img_per_row, 10 * n_img_per_row))for i in range(n_img_per_row): ix = 10 * i + 1 for j in range(n_img_per_row): iy = 10* j + 1 img[ix:ix + 8, iy:iy + 8] = X[i * n_img_per_row + j].reshape((8, 8))plt.imshow(img, cmap=plt.cm.binary) plt.title('A selection from the 64-dimensional digits dataset')
运行代码,获得X的大小是(901,64),也就是901个样本。下图显示了部分样本:
- 降维
以t-SNE为例子,代码如下,n_components设置为3,也就是将64维降到3维,init设置embedding的初始化方式,可选random或者pca,这里用pca,比起random init会更stable一些。
print("Computing t-SNE embedding") tsne = manifold.TSNE(n_components=3, init='pca', random_state=0) t0 = time() X_tsne = tsne.fit_transform(X)plot_embedding_2d(X_tsne[:,0:2],"t-SNE 2D") plot_embedding_3d(X_tsne,"t-SNE 3D (time %.2fs)" %(time() - t0))
降维后得到X_ tsne,大小是(901,3),plot_ embedding_ 2d()将前2维数据可视化,plot_ embedding_ 3d()将3维数据可视化。
函数plot_ embedding_ 3d定义如下:
def plot_embedding_3d(X, title=None): #坐标缩放到[0,1]区间 x_min, x_max = np.min(X,axis=0), np.max(X,axis=0) X = (X - x_min) / (x_max - x_min) #降维后的坐标为(X[i, 0], X[i, 1],X[i,2]),在该位置画出对应的digits fig = plt.figure() ax = fig.add_subplot(1, 1, 1, projection='3d') for i in range(X.shape[0]): ax.text(X[i, 0], X[i, 1], X[i,2],str(digits.target[i]), color=plt.cm.Set1(y[i] / 10.), fontdict={'weight': 'bold', 'size': 9}) if title is not None: plt.title(title)
- 看看效果
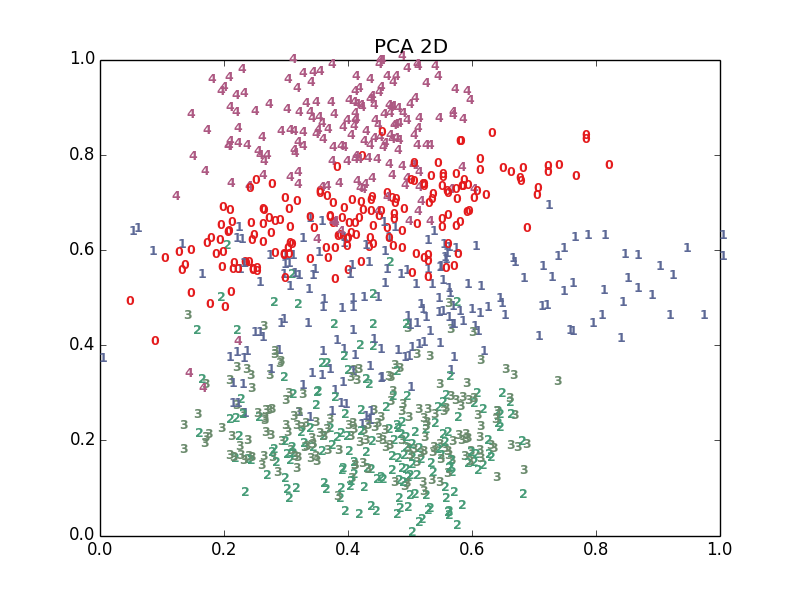
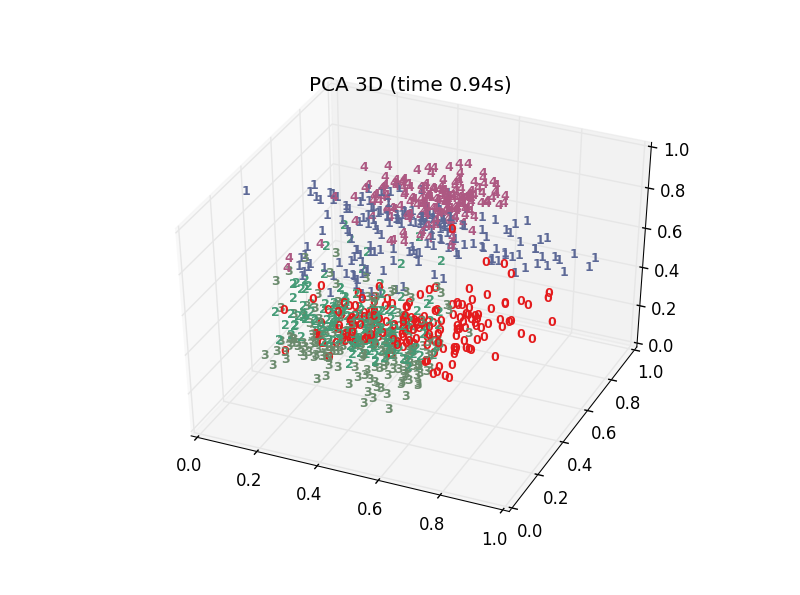
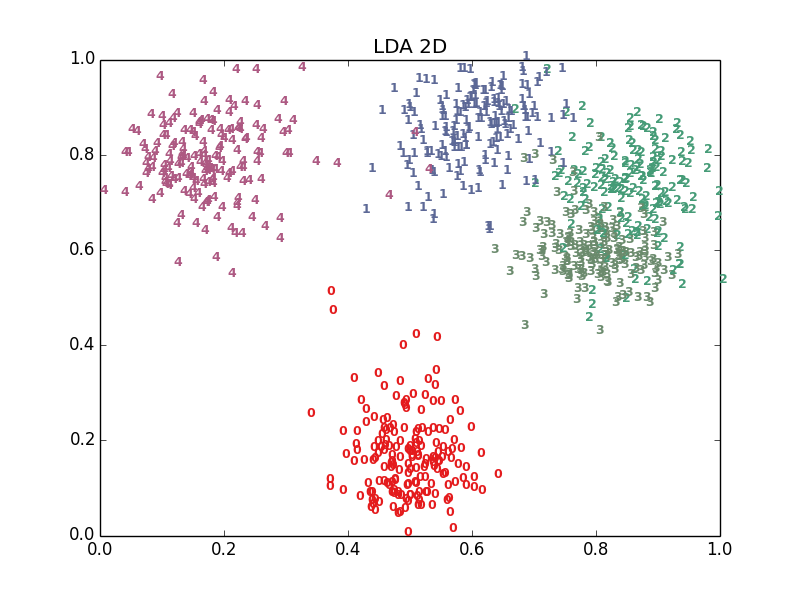
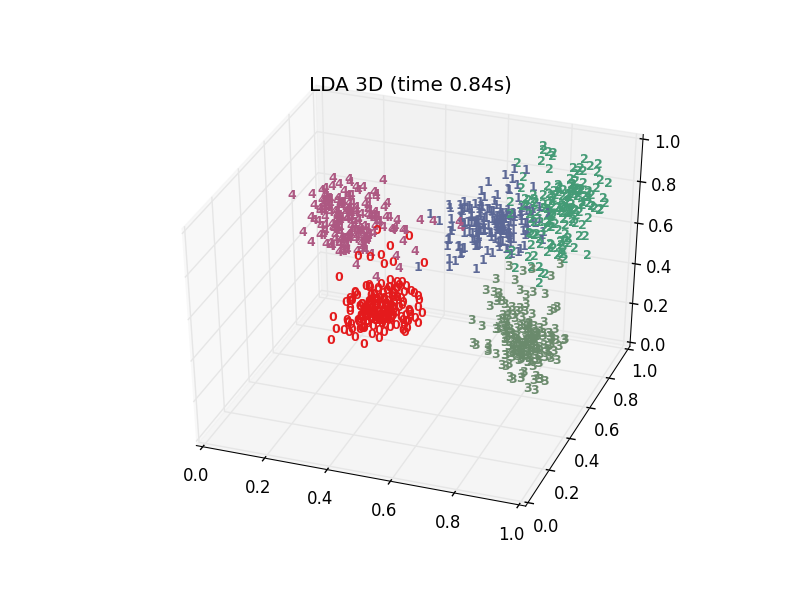
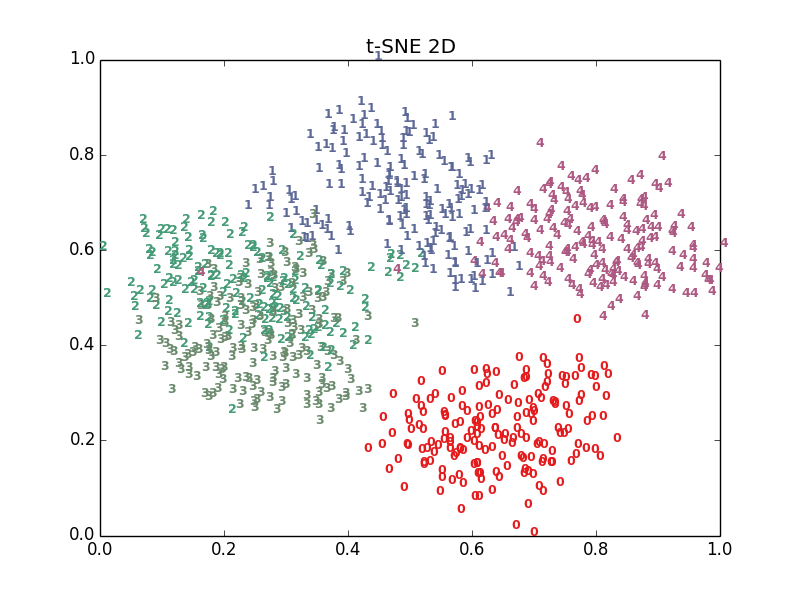
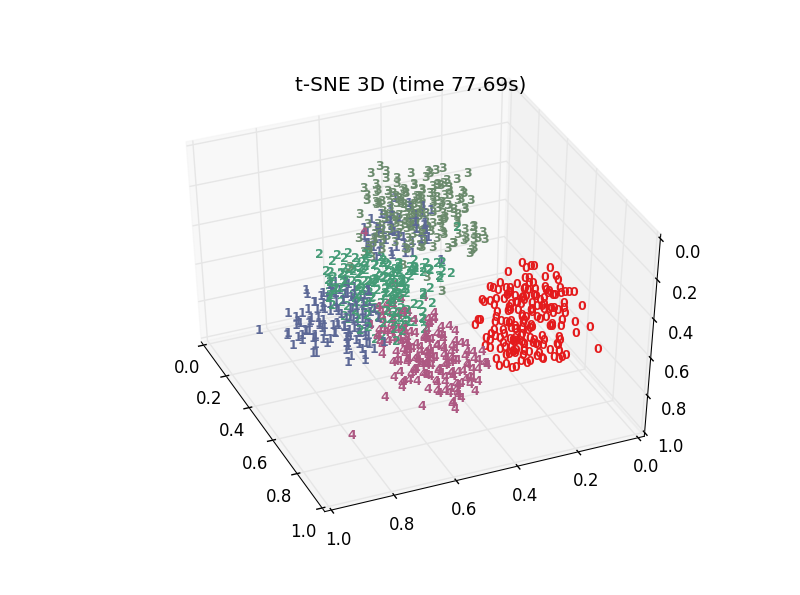
十多种算法,结果各有好坏,总体上t-SNE表现最优,但它的计算复杂度也是最高的。下面给出PCA、LDA、t-SNE的结果:
- 代码获取
MachineLearning/ManifoldLearning/DimensionalityReduction_DataVisualizing
下文转自:http://blog.csdn.net/zhangweiguo_717/article/details/70188517
SNE、TSNE
TSNE是由SNE衍生出的一种算法,SNE最早出现在2002年,它改变了MDS和ISOMAP中基于距离不变的思想,将高维映射到低维的同时,尽量保证相互之间的分布概率不变,SNE将高维和低维中的样本分布都看作高斯分布,而Tsne将低维中的坐标当做T分布,这样做的好处是为了让距离大的簇之间距离拉大,从而解决了拥挤问题。从SNE到TSNE之间,还有一个对称SNE,其对SNE有部分改进作用。
- SNE算法
- 对称SNE算法
- TSNE算法(***)
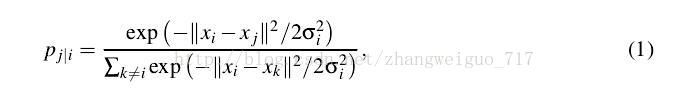

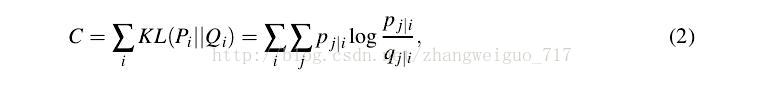
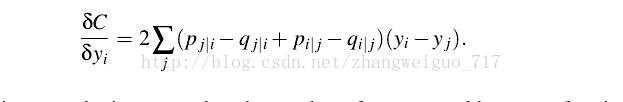
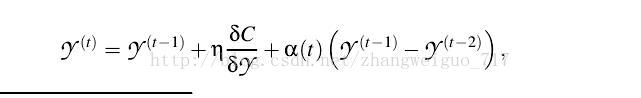
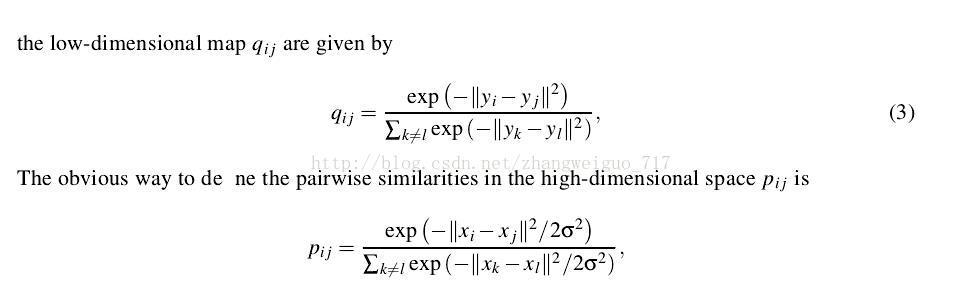
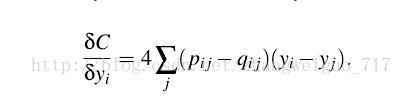
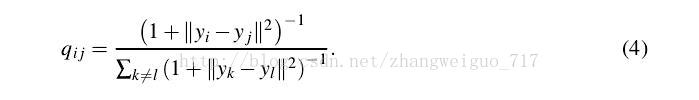
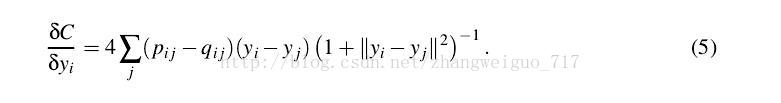
























 2086
2086

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








