朴素贝叶斯算法的参数的最大似然估计

朴素贝叶斯算法的参数的最大似然估计

设输入向量为 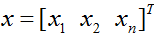。我们假定输入特征 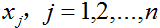是离散的、二值化的变量，即 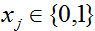。对每一个训练样例，输出对象是0或者1，即 。我们的模型由


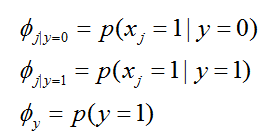
参数化。
我们把 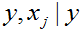建模成伯努利分布，所以这是朴素贝叶斯最简单的特例之一。
我们根据


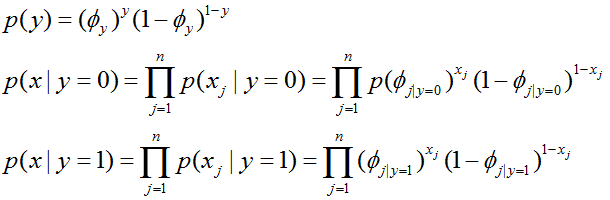
来建立 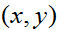的联合分布。


（1）我们先写出 。


（2）计算关于各个参数的偏导数，令其为0，求得各个参数。
先求 ，


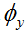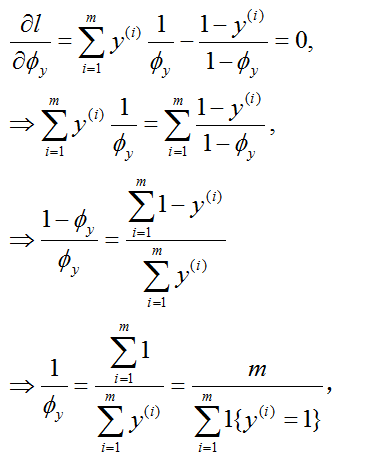
从而，


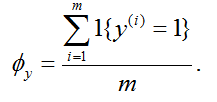
接下来求 ，


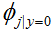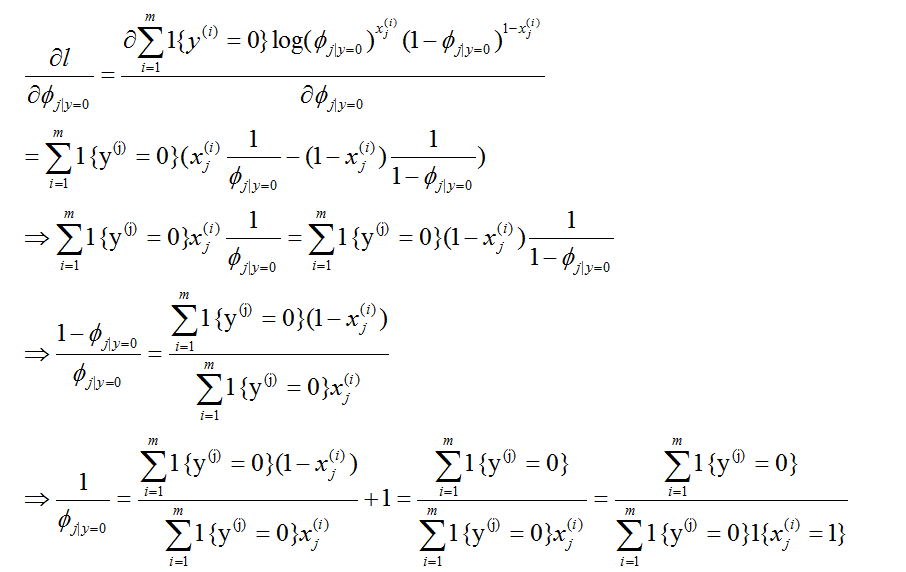
从而，


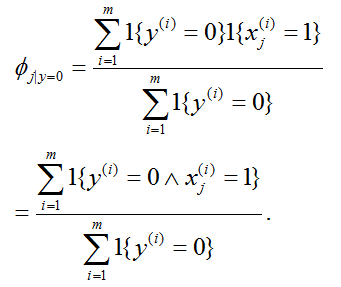
同理 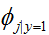的证明与上面类似，我们在这里只写出答案：





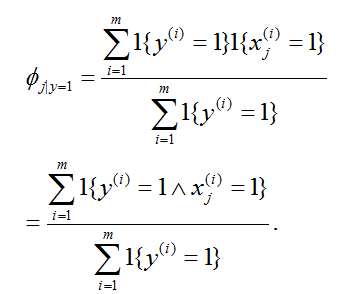
最后，我们想说明一下，我们上述建模的贝叶斯分类器，是一个线性分类器；即存在某个 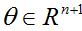使得


（假定 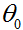是一个截距项）。
证明如下：


于是，我们可以找到:




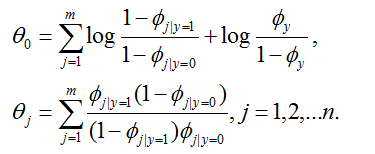
也就是说，我们拿一个新数据 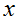代入模型测试，利用我们上面得到的线性分类器 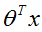，与利在朴素贝叶斯比较 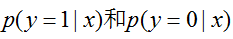是等效的。