【无人机姿态动力学模型】

在 上一篇文章中，我们得到了一条 输入量为 机体角速度， 输出量为 机体姿态的微分方程：
$$\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]=\left[\begin{array}{ccc}1& sin\varphi tan\theta & cos\varphi tan\theta \\ 0& cos\varphi & -sin\varphi \\ 0& sin\varphi /cos\theta & cos\varphi /cos\theta \end{array}\right]\left[\begin{array}{c}{\omega }_{bx}\\ {\omega }_{by}\\ {\omega }_{bz}\end{array}\right]$$
至此，为了得到动力学模型，我们还希望得到一条 输入量为 力或者力矩（对于姿态而言，肯定是力矩啦）， 输出量为 机体角速度的微分方程。下面进行分析与推导。

预备知识

符号标识说明

在下面的推导中，将会出现大量的符号，下面对符号标识进行大致说明。符号右下标，表示当前符号所归属的物理域；右上标，表示对符号进行描述的物理域。如符号${\omega }_B^O$，表示$坐标系B$的角速度在$坐标系O$中的描述。

纯转动（无平动）矢量的微分

对于纯转动（无平动）的情况，我们先讨论无限小转动的情况。

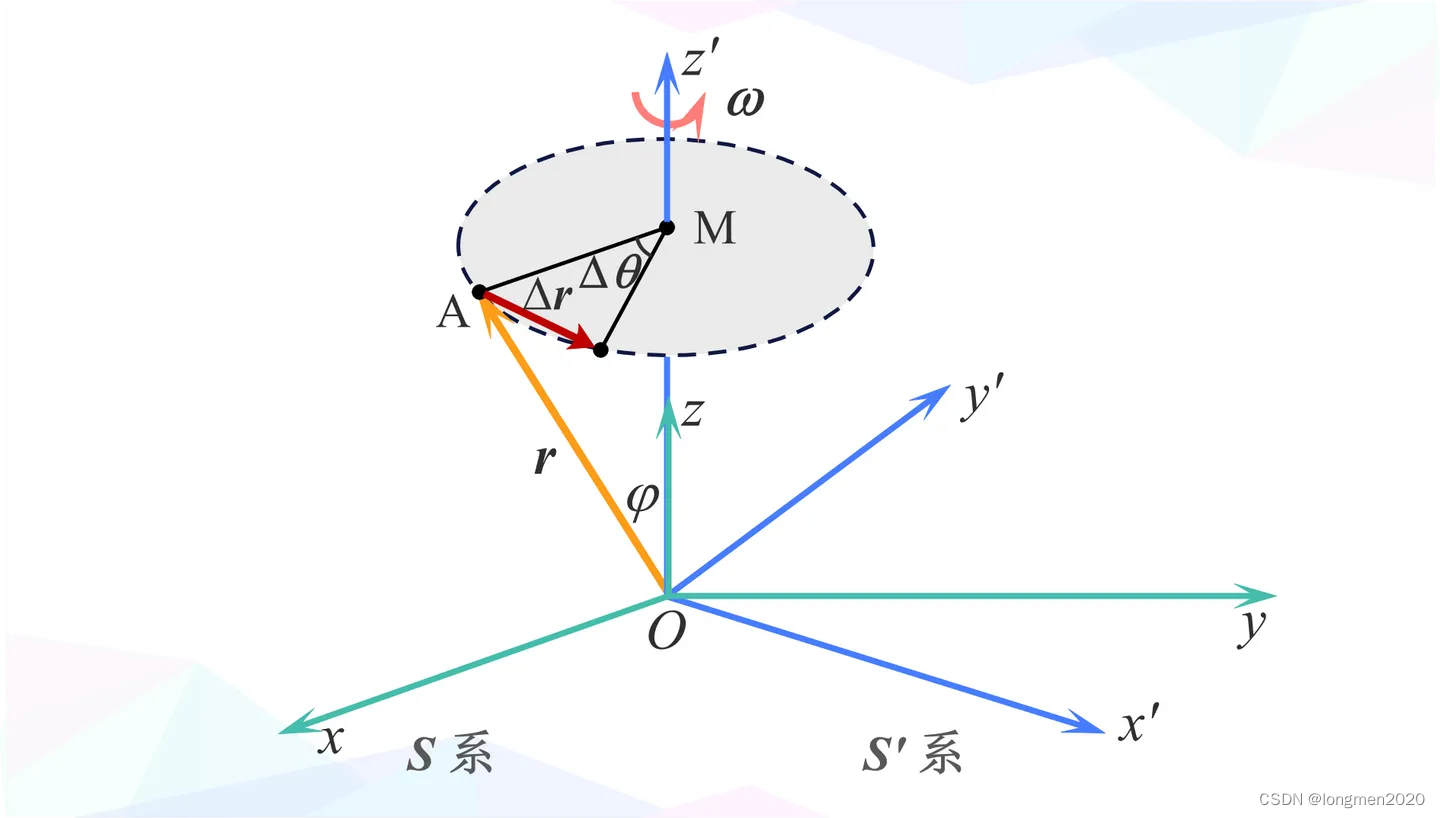
如图所示，在$参考系S$中建立直角坐标系$Oxyz$；在参考系$S^{\prime }$中，建立直角坐标系$O^{\prime }{x}^{\prime }{y}^{\prime }{z}^{\prime }$。令参考系$S$为惯性系，让$参考系S^{\prime }$相对$S系$以角速度$\omega$转动，瞬时转轴为$z^{\prime }轴$，令$Oz轴$与$O^{\prime }{z}^{\prime }轴$重合。

在极短时间$\Delta t$内，$参考系S^{\prime }$相对$S系$发生了无限小转动，角位移是$\Delta \vec{\theta }$（这是一个矢量，方向根据右手定则，指向$\overrightarrow{Oz}$的方向，大小为$\Delta \theta$）。

设某一个矢量$\vec{r}$在$S^{\prime }系$上，也跟随着$S^{\prime }系$发生了转动，得到了$\overrightarrow{r^{\prime }}$（图中未画出），矢量$\vec{r}$的变化量是$\Delta \vec{r}$。

由于$\Delta \vec{\theta }$是无限小量，那么$\Delta \vec{r}$也是无限小量，此时$\Delta \vec{r}$必与$\vec{r}$和$\Delta \vec{\theta }$构成的平面垂直。且有以下关系成立
$$\begin{array}{rl}|\Delta \vec{r}|& =\overline{AM}\cdot |\Delta \theta |\\ & =|\vec{r}|\sin \phi \cdot |\Delta \vec{\theta }|\end{array}$$
根据垂直和长度，我们可以根据叉乘的定义，将上面的关系表达为
$$\Delta \vec{r}=\Delta \vec{\theta }\times \vec{r}$$
对上式两边分别除以$\Delta t$并取极限有
$$\begin{array}{rl}\underset{\Delta t\to 0}{\lim }\frac{\Delta r}{\Delta t}& =\underset{\Delta t\to 0}{\lim }(\frac{\Delta \theta }{\Delta t}\times r)\\ & =\underset{\Delta t\to 0}{\lim }(\frac{\Delta \theta }{\Delta t})\times r\end{array}$$
其中
$$\begin{array}{rl}\underset{\Delta t\to 0}{\lim }\frac{\Delta \vec{r}}{\Delta t}& =\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=v\\ \underset{\Delta t\to 0}{\lim }\frac{\Delta \vec{\theta }}{\Delta t}& =\frac{\mathrm{d}\vec{\theta }}{\mathrm{d}t}=\omega \end{array}$$所以
$$\boxed{\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\omega \times \vec{r}=v}$$其中，$v$可以表示为这个矢量的速度。

可见，一个$非惯性系S^{\prime }$对一个$惯性系S$做纯转动时，$非惯性系S^{\prime }$上跟随转动的某一矢量$\vec{r}$的微分可以表示为转动的角速度$\omega$和矢量本身$\vec{r}$的叉乘；又因为微分可以看作是速度，而矢量$\vec{r}$又是跟随着$非惯性系S^{\prime }$转动，那么$\omega \times \vec{r}$又可以看作是$非惯性系S^{\prime }$于$惯性系S$的牵连速度。

一般平面运动（转动+平动）矢量的微分（科里奥利公式）

• 定性分析
  首先，可以不失一般性地假设所研究的矢量是表达位移的矢量（即位矢），那么对位矢的微分，得到的便是速度矢量。我们可以假设所研究的位矢在一个非惯性系上（比如无人机的机体坐标系），这时候位矢的所有平面运动，都可以分解成位矢跟随非惯性系对惯性系的转动+位矢在非惯性系上的平动。
  有一个概念是很显然的：
  $$绝对速度=相对速度+牵连速度$$
  所以我们可以说，对于任何位矢$\vec{P}$在$非惯性系B$中，$非惯性系B$相对于$惯性系O$的纯转动角速度是${\omega }_B^O$的情况，结合前面纯转动（无平动）矢量的微分分析结尾的结论：
  $$\boxed{\frac{\mathrm{d}{\vec{P}}^O}{\mathrm{d}t}=\frac{\mathrm{d}\overrightarrow{P^B}}{\mathrm{d}t}+{\omega }_B^O\times {\vec{P}}^O}$$
  其中位矢$\vec{P}$在$惯性系O$下的微分$\frac{\mathrm{d}{\vec{P}}^O}{\mathrm{d}t}$便是绝对速度，$\vec{P}$在$非惯性系B$下的微分$\frac{\mathrm{d}{\vec{P}}^B}{\mathrm{d}t}$便是相对速度，${\omega }_B^O\times {\vec{P}}^O$便是$非惯性系B$于$惯性系O$的牵连速度。

• 严格推导
  严格的推导可以查阅：【清华大学 理论力学 高云峰】 【精准空降到 04:53】 ，此处不赘述。

• 推广至矩阵形式
  上面是对矢量进行讨论，我们知道矢量是可以用列矩阵来表示的，如3维矢量可以用3行1列的列矩阵来表示，那么m行n列的矩阵，可以视作n个m维矢量的合集。假设当前存在矩阵$\mathbb{M}=\left[\begin{array}{cccc}{\vec{r}}_{m1}& {\vec{r}}_{m2}& \cdots & {\vec{r}}_{mn}\end{array}\right]$，则
  $$\begin{array}{rl}\dot{\mathbb{M}}& =\left[\begin{array}{cccc}\frac{\mathrm{d}{\vec{r}}_{m1}^O}{\mathrm{d}t}& \frac{\mathrm{d}{\vec{r}}_{m2}^O}{\mathrm{d}t}& \cdots & \frac{\mathrm{d}{\vec{r}}_{mn}^O}{\mathrm{d}t}\end{array}\right]\\ & =\left[\begin{array}{cccc}\frac{\mathrm{d}{\vec{r}}_{m1}^B}{\mathrm{d}t}+\omega \times {\vec{r}}_{m1}^O& \frac{\mathrm{d}{\vec{r}}_{m2}^B}{\mathrm{d}t}+\omega \times {\vec{r}}_{m2}^O& \dots & \frac{\mathrm{d}{\vec{r}}_{mn}^B}{\mathrm{d}t}+\omega \times {\vec{r}}_{mn}^O\end{array}\right]\end{array}$$其中，可以看作有n个m维矢量做一般平面运动，分解为：跟随着$非惯性系B$相对于$惯性系O$做角速度为$\omega$的纯转动的同时，在$非惯性系B$内做相对速度是$\frac{\mathrm{d}{\vec{r}}_{mi}^B}{\mathrm{d}t}$的平动。至此，对于这样作为矢量集合的矩阵的微分，我们也找到了表示方法。

刚体转动欧拉方程的推导

根据角动量定理，可以得到
$$M^O=\frac{\mathrm{d}}{\mathrm{d}t}(J^O{\omega }_B^O)$$其中$M^O$是无人机机体在$惯性系O$下受到的合外力矩，$J^O$是机体转动惯量3*3矩阵在$惯性系O$下的表达，${\omega }_B^O$是和$非惯性系B$固连的机体角速度在$惯性系O$下的表达。

根据求导链式法则（用符号上加点代表对符号进行微分）
$$\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}t}(J^O{\omega }_B^O)& =\dot{J^O}{\omega }_B^O+J^O\dot{{\omega }_B^O}\end{array}$$其中，分析3*3转动惯量矩阵的微分$\dot{J^O}$
$$\dot{J^O}=\left[\begin{array}{ccc}\dot{J_1^B}+{\omega }_B^O\times J_1^O& \dot{J_2^B}+{\omega }_B^O\times J_2^O& \dot{J_3^B}+{\omega }_B^O\times J_3^O\end{array}\right]$$又因为当机体构型固定后，机体转动惯量在机体$非惯性系B$的表达不变，即$\dot{J_i^B}\equiv 0$，所以
$$\begin{array}{rl}\dot{J^O}& =\left[\begin{array}{ccc}{\omega }_B^O\times J_1^O& {\omega }_B^O\times J_2^O& {\omega }_B^O\times J_3^O\end{array}\right]\\ & ={\omega }_B^O\times \left[\begin{array}{ccc}{J}_1^O& J_2^O& J_3^O\end{array}\right]\\ & ={\omega }_B^O\times J^O\end{array}$$因此可以推出刚体转动欧拉方程为
$$\boxed{M^O=\frac{\mathrm{d}}{\mathrm{d}t}(J^O{\omega }_B^O)={\omega }_B^O\times J^O{\omega }_B^O+J^O\dot{{\omega }_B^O}}$$

无人机姿态动力学模型

我们希望得到一条输入量为力或者力矩（对于姿态而言，肯定是力矩啦），输出量为机体角速度的微分方程为作为姿态动力学模型，同时，因为在机体坐标系研究姿态更直观，所以姿态动力学模型中的参数最好是在机体坐标系下的表达。则输出量为${\omega }_B$,输入量为$M^B$。
首先对于$L=J\omega$，有
$$\begin{array}{rl}{L}^B& =J^B{\omega }^B\\ L^O& =J^O{\omega }^O\\ & =J^O{R}_B^O{\omega }^B\\ & =R_B^O{L}^B\\ & =R_B^O{J}^B{\omega }^B\end{array}$$
所以可以得到
$$\begin{array}{rl}{J}^O{R}_B^O{\omega }_B& =R_B^O{J}^B{\omega }^B\\ J^O& =R_B^O{J}^B{R_B^O}^{-1}\end{array}$$
则由刚体转动欧拉方程
$$\begin{array}{rl}{M}^O& ={\omega }_B^O\times J^O{\omega }_B^O+J^O\dot{{\omega }_B^O}\\ R_B^O{M}^B& =(R_B^O{\omega }_B)\times (R_B^O{J}^B{R_B^O}^{-1})R_B^O{\omega }_B+R_B^O{J}^B{R_B^O}^{-1}\dot{(R_B^O{\omega }_B)}\\ R_B^O{M}^B& =R_B^O[{\omega }_B{]}_{\mathrm{x}}{R_B^O}^{-1}{R}_B^O{J}^B{\omega }_B+R_B^O{J}^B{R_B^O}^{-1}\dot{(R_B^O{\omega }_B)}\\ M^B& =[{\omega }_B{]}_{\mathrm{x}}{J}^B{\omega }_B+J^B{R_B^O}^{-1}(\dot{R_B^O}{\omega }_B+R_B^O\dot{{\omega }_B})\end{array}$$
根据【旋转矩阵】对旋转矩阵导数的推导，可以知道$\dot{R_B^O}={\omega }_B^O\times R_B^O=[{\omega }_B^O{]}_{\mathrm{x}}{R}_B^O=R_B^O[{\omega }_B{]}_{\mathrm{x}}{R_B^O}^{-1}{R}_B^O=R_B^O[{\omega }_B{]}_{\mathrm{x}}$，则
$$\begin{array}{rl}{M}^B& =[{\omega }_B{]}_{\mathrm{x}}{J}^B{\omega }_B+J^B{R_B^O}^{-1}(\dot{R_B^O}{\omega }_B+R_B^O\dot{{\omega }_B})\\ M^B& =[{\omega }_B{]}_{\mathrm{x}}{J}^B{\omega }_B+J^B{R_B^O}^{-1}(R_B^O[\omega {]}_{\mathrm{x}}{\omega }_B+R_B^O\dot{{\omega }_B})\\ M^B& ={\omega }_B\times J^B{\omega }_B+J^B{R_B^O}^{-1}(R_B^O{\omega }_B\times {\omega }_B+R_B^O\dot{{\omega }_B})\end{array}$$
又根据叉乘的定义，$a\times a=0$，则
$$\begin{array}{rl}{M}^B& ={\omega }_B\times J^B{\omega }_B+J^B{R_B^O}^{-1}{R}_B^O\dot{{\omega }_B}\\ M^B& ={\omega }_B\times J^B{\omega }_B+J^B\dot{{\omega }_B}\end{array}$$
由此便在机体坐标系下建立了姿态动力学模型。又因为$M^B=\mathbf{\tau }+{\mathbf{G}}_{\mathbf{a}}$，其中$\mathbf{\tau }$为螺旋桨为机体提供的力矩，${\mathbf{G}}_{\mathbf{a}}$为机体的陀螺力矩，则姿态动力学模型又可以表达为
$$\mathbf{\tau }+{\mathbf{G}}_{\mathbf{a}}={\omega }_B\times J^B{\omega }_B+J^B\dot{{\omega }_B}$$