考研高数重难点：连续，存在，可导，有定义，左右连续，左右导数名词辨析。极限，连续，导数存在性辨析。

一只轩666

已于 2024-05-23 11:55:33 修改

阅读量8.2k

点赞数 42

文章标签：抽象代数

于 2024-05-23 11:46:54 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/zjx15296694073/article/details/139133326

版权

一、存在

1、函数在x=a处存在：

$\Leftrightarrow$ x=a在函数的定义域中，函数在x=a处有定义，函数在x=a处有图像。

2、极限在x=a处存在：

$\Leftrightarrow$ $\lim_{x \to a }$ $f(x)$ =A(具体的数)

$\Leftrightarrow$ $f(x)$ 在x=a的去心邻域有定义（但不一定）

3、导数在 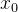$x$ = $x_0$ 处存在：

$\Leftrightarrow$ 这个极限 ${f}'$ $(x_0)$ = $\lim_{x \to0 }$ $\frac{f(x)-f(x_{0})}{x-x_0}$ =A存在

二、连续（研究在某个点处的连续性）

1、函数在x=a处连续：

图像不断

1、 $\lim_{x \to a }$ $f(x)$ =A极限存在

2、 $f(x)$ 在x=a处有定义（ $f(a)$ 存在）

3、 $\lim_{x \to a }$ $f(x)$ =A= $f(a)$

2、函数在x=a处左连续：

x=a这个点处的图像和左边不断

1、 $\lim_{x \to a ^{-}}$ $f(x)$ =A极限存在

2、 $f(x)$ 在x=a处有定义（ $f(a)$ 存在）

3、 $\lim_{x \to a ^{-}}$ $f(x)$ =A= $f(a)$

2、函数在x=a处右连续：

x=a这个点处的图像和右边不断

1、 $\lim_{x \to a ^{+}}$ $f(x)$ =A极限存在

2、 $f(x)$ 在x=a处有定义（ $f(a)$ 存在）

3、 $\lim_{x \to a ^{+}}$ $f(x)$ =A= $f(a)$

两组条件

三、可导（研究在某个点处的可导性）

1、函数在x=a处可导：

${f}'$ $(x_0)$ = $\lim_{x \to x_0}$ $\frac{f(x)-f(x_{0})}{x-x_0}$ =A这个极限存在

2、函数在x=a处有左导数：

$f_{-}^{'}$ $_{}^{}$ $(x_0)$ = $\lim_{x \to x_0^{+}}$ $\frac{f(x)-f(x_{0})}{x-x_0}$ =A这个极限存在

3、函数在x=a处有右导数：

$f_{+}^{'}$ $_{}^{}$ $(x_0)$ = $\lim_{x \to x_0^{-}}$ $\frac{f(x)-f(x_{0})}{x-x_0}$ =A这个极限存在

【注】在某点处连续或者可导，研究是在某点处，不包括这个点的去心领域哦

下面两条的具体证明方法稍后会补上，属于强化内容

这两条在使用洛必达法则时至关重要的，用来判断洛必达法则使用规则的第二条：要求在x=a的去心邻域可导

1、在某点处连续不一定在它的去心邻域也连续

记得吗连续的定义第一条是：

$\lim_{x \to a }$ $f(x)$ =A极限存在

【只说极限存在哦，而极限存在的定义是： $f(x)$ 在x=a的去心邻域有定义。而有定义不代表在去心邻域连续】

2、在某点处可导不一定在它的去心邻域也可导

可导说明 ${f}'$ $(x_0)$ = $\lim_{x \to x_0}$ $\frac{f(x)-f(x_{0})}{x-x_0}$ =A这个极限存在，极限存在说明去心邻域有定义，去心邻域有定义不代表就可导

可导 $\Rightarrow$ ${f}'$ $(x_0)$ = $\lim_{x \to x_0}$ $\frac{f(x)-f(x_{0})}{x-x_0}$ =A这个极限存在 $\Rightarrow$ 去心邻域有定义 $\neq$ 去心邻域可导

四、混合名词辨析（考验语文水平）

1、知识点

函数在x=a这个点处可导 $\Rightarrow$ 函数在x=a这个点处连续（可导必连续，但连续不一定可导）

但函数在x=a这个点处连续推不出函数在x=a这个点处可导（绝对值函数连续但在x=a处不可导）

2、判断题（两个要点：看好每句话的主语，推到好关系）

若 $f(x)$ 在x=a处连续 $\Rightarrow$ $f(x)$ 在x=a的邻域有定义（T）

若 $f(x)$ 在x=a的邻域有定义 $\Rightarrow$ $f(x)$ 在x=a处连续（F）

若 $f(x)$ 在x=a的处有定义 $\Rightarrow$ $f(x)$ 在x=a处连续（F）

若 $f'(x)$ 在x=a的处有定义 $\Rightarrow$ $f(x)$ 在x=a处连续（T）

若 $f'(x)$ 在x=a的处有定义 $\Rightarrow$ $f'(x)$ 在x=a处连续（F）

若 $f(x)$ 在x=a的处可导 $\Rightarrow$ $f(x)$ 在x=a处连续（T）

若 $f'(x)$ 在x=a的处可导 $\Rightarrow$ $f'(x)$ 在x=a处连续（T）

若 $f''(x)$ 在x=a的处可导 $\Rightarrow$ $f''(x)$ 在x=a处连续（T）

若 $f(x)$ 在x=a的处可导 $\Rightarrow$ $f'(x)$ 在x=a处连续（F）

若 $f'(x)$ 在x=a的处可导 $\Rightarrow$ $f(x)$ 在x=a处连续（T）

同阶可导可推同阶连续

高阶可导可推低阶连续

但是低阶可导不能推高阶连续

若 ${f}'$ $(a)$ 存在 $\Rightarrow$ $f'(x)$ 在x=a处连续（F）

若 ${f}'$ $(a)$ 存在 $\Rightarrow$ $f(x)$ 在x=a处连续（T）

若 $f''(a)$ 存在 $\Rightarrow$ $f'(x)$ 在x=a处连续（T）

$\Rightarrow$ $f(x)$ 在x=a处连续（T）

五、极限，连续，导数存在性辨析

根据极限的四则运算

六、例题

评论 2

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。