二次规划（quadratic programming）

1定义

二次规划是指，带有二次型目标函数和约束条件的最优化问题。
二次规划的一般形式可以表示为，如下图1式子。

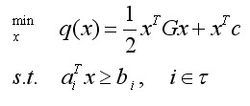
公式 1
其中G是Hessian矩阵，τ是有限指标集，c，x和{ai}，都是R中的向量。
如果Hessian矩阵是半正定的，则我们说式 1是一个凸二次规划，存在全局最优解；
如果Hessian矩阵是正定的，则存在全局唯一最优解；
如果Hessian矩阵是非正定的，则为非凸二次规划，存在多个平稳点和局部极小值点。

2 小知识

2.1 正定矩阵

设A是n阶实对称矩阵， 如果对任意一非零实向量X，都使二次型

$$f(X)= X^TMX>0,$$
则称f(X)为正定二次型，矩阵A称为正定矩阵(Positive Definite)。

2.2 Hessian矩阵

suppose f : $ℝ^n$ → ℝ is a function taking as input a vector x ∈ $ℝ^n$ and outputting a scalar f(x) ∈ ℝ; if all second partial derivatives of f exist and are continuous over the domain of the function, then the Hessian matrix H of f is a square n×n matrix, usually defined and arranged as follows:

or, component-wise:

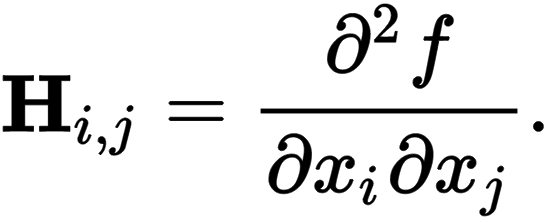
简单记忆：Hessian矩阵就是二阶偏导数构成的对称矩阵。