有些变换仅用一种基本变换是不能实现的,必须由两种或多种基本变换组合才能实现。这种由多种基本变换组合而成的变换称之为复合变换,相应的变换矩阵称作为复合变换矩阵。
比如:已知三角形各顶点坐标为(10, 10),(10, 30),(30, 15),对其进行下列变换,试写出复合变换矩阵。
(1)沿X方向平移20,沿Y方向平移15,再绕原点旋转90度。
(2)绕原点旋转90度,沿X方向平移20,沿Y方向平移15。
(3)沿X方向放大2倍,Y方向缩小3倍,关于原点对称,绕原 点旋转180度。
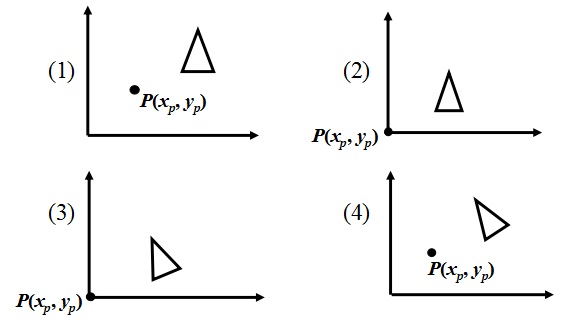
1.绕任意点P(xp, yp)作旋转变换,旋转角度为θ。
将旋转中心P(xp, yp)平移到坐标原点,变换矩阵为:
绕坐标原点旋转θ角,变换矩阵为:
将旋转中心P(xp, yp)平移回原来的位置,变换矩阵为:
因此,绕任意点P(xp, yp)旋转的复合变换矩阵为:
2.相对于任意点P(xp, yp)作比例变换,比例系数为(Sx, Sy),即P点不变的比例变换。
将点P(xp, yp)平移至坐标原点,变换矩阵为:
相对于坐标原点作比例变换,变换矩阵为:
将点P(xp, yp)平移回原来位置,变换矩阵为:
因此,相对于任意点P(xp, yp)作比例变换的复合变换矩阵为: T = T1*T2*T3
3.相对于任意点P(xp, yp)作对称变换
将点P(xp, yp)平移至坐标原点,变换矩阵为:
相对于坐标原点作对称变换,变换矩阵为:
将点P(xp, yp)平移回原来位置,变换矩阵为:
因此,相对于任意点P(xp, yp)作对称变换的复合变换矩阵为:T = T1*T2*T3
4.关于任意直线作对称变换,直线方程为y=mx+b
平移直线(以沿Y轴平移为例),使其通过坐标原点,变换矩阵为:
绕原点顺时针旋转角,使其与X轴重合(其中,tgθ=m)
关于X轴作对称变换,变换矩阵为:
绕原点逆时针旋转角(即作第(2)步的逆运算),变换矩阵为:
平移直线,使其回到原来位置(即作第(1)步的逆运算),变换矩阵为:
因此,关于任意直线作对称变换的复合变换矩阵为: T = T1*T2*T3*T4*T5
综上所述,复合变换是通过基本变换组合而成的。
注意:由于矩阵乘法不适用于交换律,即AB≠BA,因此组合的顺序是不能颠倒的,顺序不同,则变换结果不同。









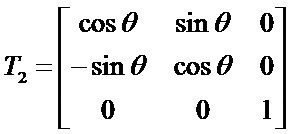
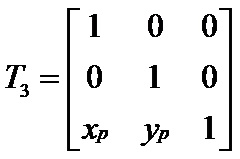
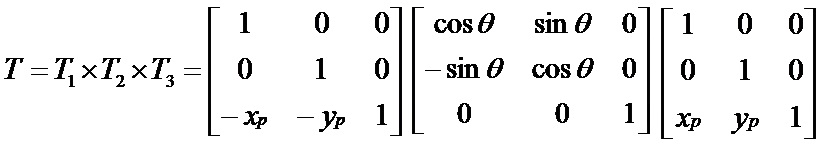
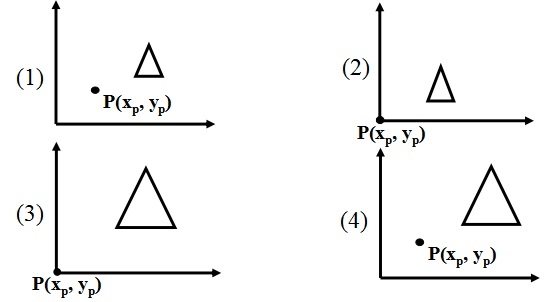
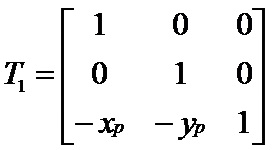
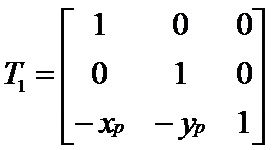
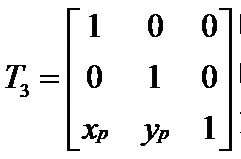
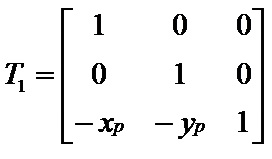
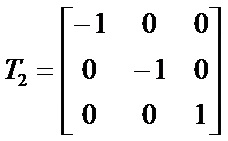
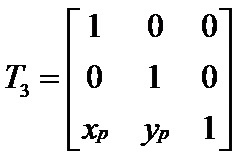
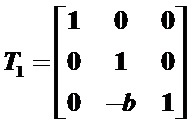
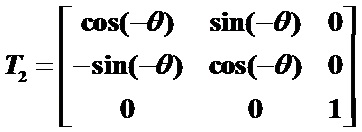
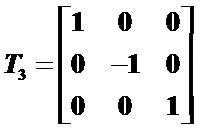
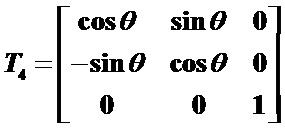

















 1395
1395

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








