【论文笔记】CIRNet：基于CycleGAN的无监督循环配准模型

本文是论文《UNSUPERVISED THREE-DIMENSIONAL IMAGE REGISTRATION USING A CYCLE CONVOLUTIONAL NEURAL NETWORK》的阅读笔记。

文章提出了一个无监督的循环图像配准网络CIRNet，它由两个配准模块组成，两者具有相同的结构，并且共享参数。此外加入了循环一致性损失来为确保预测形变场的精度而提供额外的约束。文章在4D(3D+t)心脏CT数据集和MRI数据集上分别做了实验，验证了模型的有效性。简单来说就是将CycleGAN引入到了VoxelMorph模型中。

一、配准问题介绍

有监督的配准方法容易收到有监督信息中存在的误差和错误的影响，基于patch的配准方法训练时更快，但不能充分利用全局信息。

配准问题可以简化为一个优化问题，即最小化以下能量函数$P$：
$$P=S(M(\varphi ),F)+\mathrm{Reg}(\varphi )$$
其中，$M$和$F$分别表示浮动图像和固定图像，$\varphi$表示形变场，$M(\varphi )$表示根据形变场变形后的浮动图像，函数$S(x,y)$表示两幅图像之间的不相似性，$Reg(\varphi )$表示形变场的平滑正则化项。

二、网络结构

从下图可以看出，CIRNet由两个级联的配准模块$R_1，R_2$组成，两者具有相同的结构，并且共享参数，这样模型参数不会增加很多。

上图中，$A$和$B$分别表示浮动图像和固定图像，$A({\varphi }_1)$是根据形变场${\varphi }_1$变形后的浮动图像，$A({\varphi }_1\circ {\varphi }_2)$是先根据${\varphi }_1$变形再根据${\varphi }_2$变形后的浮动图像，$L_{cyc}$是循环一致性损失。配准模块$R_1$是将浮动图像$A$配准到固定图像$B$，得并使得$A({\varphi }_1)$与$B$尽可能的像；配准模块$R_2$是将变形后的浮动图像$A({\varphi }_1)$配准到固定图像$A$，得并使得$A({\varphi }_1\circ {\varphi }_2)$与$A$尽可能的像。

CIRNet是在VoxelMorph的基础上加以改进的，所以每个配准模块的结构和VoxelMorph相同，如下图。

三、损失函数

网络的损失有三个：$L_{NCC}、L_{cyc}、L_{reg}$。

归一化的互相关$L_{NCC}$，它用来衡量图像$A({\varphi }_1)$和图像$B$之间的相似性，它是通过大小为$9\times 9\times 9$的滑动窗口来计算的，当$L_{NCC}$接近于0时，说明两张图像不相关，反之接近于1时说明两张图像正相关。

循环一致性损失$L_{cyc}$可以让图像$A({\varphi }_1\circ {\varphi }_2)$和图像$A$尽可能的相似。此外考虑到两幅图像还应该在灰度值分布上相同，所以在循环一致性损失中加入了$L_2$正则项。其表达式如下：
$$L_{cyc}\left(A\left({\varphi }_1\circ {\varphi }_2\right),A\right)=\frac{1}{N}\sum _{i\in \Omega }{\left(A\left({\varphi }_1\circ {\varphi }_2\right)(i)-A(i)\right)}^2$$
其中，$N$是体素的数量，$\Omega$表示图像中的所有体素。

形变场的平滑正则项损失$L_{reg}$定义如下：
$$L_{reg}(\varphi )=\sum _{i\in \Omega }\nabla \varphi (i{)}^2$$
综上，配准模块$R_1、R_2$的总损失为：
$$\begin{array}{rl}{L}_{R1}(A,B)=-& L_{NCC}\left(A\left({\varphi }_1\right),B\right)\\ & +\alpha L_{reg}\left({\varphi }_1\right)+\beta L_{cyc}\left(A\left({\varphi }_1\circ {\varphi }_2\right),A\right)\\ L_{R2}\left(A\left({\varphi }_1\right),A\right)& =-L_{NCC}\left(A\left({\varphi }_1\circ {\varphi }_2\right),A\right)\\ & +\alpha L_{reg}\left({\varphi }_2\right)+\beta L_{cyc}\left(A\left({\varphi }_1\circ {\varphi }_2\right),A\right)\end{array}$$
其中$\alpha 、\beta$是平衡因子。

四、实验

第一个数据集是ACDC数据集，是一个4D的心脏电影MRI数据集，第二个数据是心脏的CTA图像。训练时使用Adam作为优化器，学习率在前100个epoch为0.0001，没50个epoch线性减少。batch size在第一个数据集为8，第二个数据集为1。$\alpha =1，\beta =5$。使用的baseline是传统的B样条非刚性配准算法Elastix和基于学习的配准模型VoxelMorph，评价指标选用的是DSC（Dice相似性系数）。

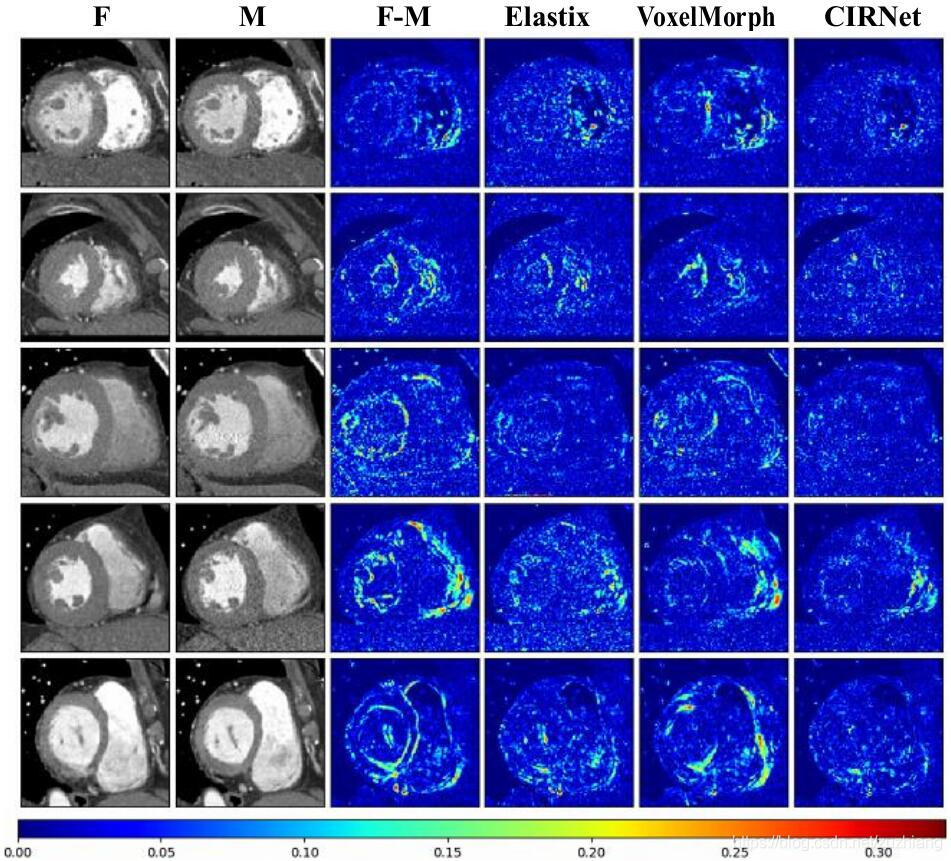
下图是各个配准方法的对比结果。

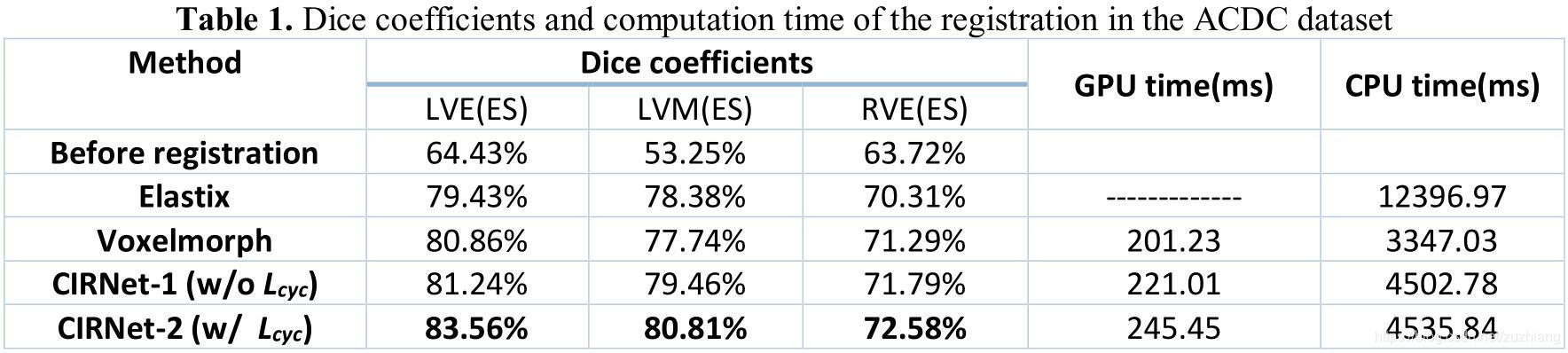
下图是评价指标和运行时间的对比，可以发现CIRNet取得了最好的效果。