动力电池SOC和SOH估计
动力电池SOC和SOH估计是动力电池管理系统的核心功能之一,精确的SOC和SOH估计可以保障动力电池系统安全可靠地工作,优化动力电池系统,并为电动汽车的能量管理和安全管理等提供依据。然而,动力电池具有可测参数量有限且特性耦合、即用即衰、强时变、非线性等特征,车载环境应用又面临串并联成组非均一复杂系统、全工况(宽倍率充放电)、全气候(-30~45℃温度范围)应用需求,高精度、强鲁棒性的动力电池SOC和SOH估计极具挑战,一直是行业技术攻关的难点和国际学术界研究的前沿热点。本章将系统阐述动力电池SOC和SOH估计的基础理论和应用,并讨论静态容量已知和动态容量在线估计条件下动力电池SOC估计性能,以及SOH与SOC协同估计的必要性,并提供以便BMS现实应用的详细算法流程。
SOC估计
新能源汽车动力电池的SOC相当于普通燃油汽车的油表,SOC作为能量管理的重要决策因素之一,对于优化整车能量管理、提高动力电池容量和能量利用率、防止动力电池过充电和过放电、保障动力电池在使用过程中的安全性和长寿命等起着重要作用。本节将详细阐述动力电池静态容量已知情况下的SOC估计方法。
SOC估计分类
动力电池结构复杂,电化学反应过程和反应阶段复杂且难以确定,而且车载工况恶劣、多变,作为隐性状态量的SOC精确值难以得到,常见的动力电池SOC估计方法大致可分为四类:基于表征参数的方法、安时积分法、基于模型的方法以及基于数据驱动的方法,如图所示。
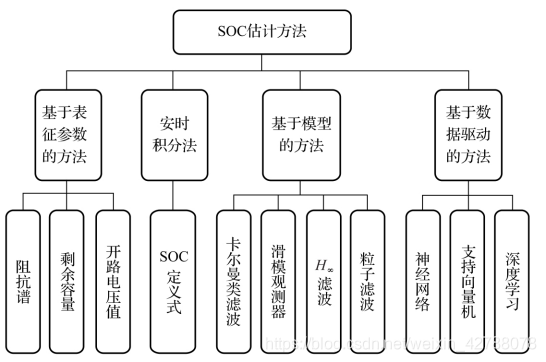
SOC估计方法的分类
1.基于表征参数的方法
该方法主要分为两步:
①建立动力电池表征参数与SOC的离线关系。
②实时计算动力电池表征参数值,并以之标定动力电池SOC。
该方法的应用需满足两个前提:所建立表征参数与SOC的离线关系应该相对稳定,所选表征参数应该是易获取的。可选表征参数包括当前剩余容量、阻抗谱、OCV等。
当前剩余容量可通过放电实验法得到,该方法被认为是确定动力电池SOC最为直接的方法。但是新能源汽车在运行中难以进行长时间的恒流放电来确定剩余容量,使得该方法仅适用于实验室等特定环境。基于阻抗谱的方法则需要借助电化学工作站来测试动力电池不同SOC值的阻抗,并制定SOC和参数的映射关系,进而采用查表的方式完成SOC的标定。相对稳定的OCV-SOC关系常被工业界用来标定动力电池SOC,大量的BMS产品也使用这一关系来标定动力电池初始SOC,但OCV的准确直接测量要求动力电池静置足够长的时间,因而在实际中往往需要与OCV在线辨识方法结合使用。
2.安时积分法
该方法又称为库仑计数法,即利用SOC定义估计动力电池SOC:

式中,z ( t ) z(t)z(t)表示t时刻下的动力电池SOC估计值;z ( t 0 ) z(t0)z(t0)表示动力电池SOC初始值;η i ηiηi表示动力电池充放电库仑效率,其值通过实验确定,对于锂离子动力电池而言,放电效率通常视为1,充电效率为0.98~1(充电电流3C以内);i L ( τ ) iL(τ)iL(τ)为τ时刻下动力电池充放电电流;C m a x CmaxCmax表示当前条件下动力电池的最大可用容量。
作为目前动力电池SOC计算的核心方法,安时积分法经典易用,应用最为广泛。但它主要存在三个缺陷:
①动力电池初始SOC的精确值难以获得。
②该方法对于电流传感器的精度要求很高。但在实际应用中,电流传感器的精度经常受噪声、温度漂移及其他未知随机扰动的影响。在积分计算中,这些随机量容易造成累加误差,控制器的四舍五入计算也会产生一定的影响。
③动力电池性能衰退造成其静态容量的退化,从而影响SOC的计算精度。
以上三个因素相互影响,进一步降低了该方法的可靠性。为避免以上因素的制约并提高计算精度,需要复杂烦琐的定期标定。为此,该方法经常与其他方法综合使用。例如,使用OCV确定动力电池初始SOC,使用安时积分法计算后续的SOC轨迹。
3.基于模型的估计方法
该方法利用模型和状态估计算法完成动力电池的SOC估计,因此该方法首先需要建立可靠的性能模型,本章主要以等效电路模型为例介绍基于模型的动力电池SOC估计方法。基于建立的动力电池等效电路模型及其状态方程,应用滤波算法和观测器,搭建基于模型的SOC估计算法框架,具体实施流程如图所示,包括:
①基于上一时刻的SOC值或初始SOC与电流测量值,利用安时积分来计算当前时刻的SOC预估值。
②基于模型参数-SOC关系式计算此时模型参数值,如OCV-SOC关系。
③基于模型端电压-参数关系式计算此时模型端电压。
④基于电压测量值,获取模型端电压误差,即新的信息,简称新息。
⑤以新息的一定增益(倍率)来修正上述SOC预估值,从而获取最终的SOC修正值,并将其用于下一时刻的输入。

步骤⑤中增益的表现形式取决于所采用的状态估计算法。显然,基于模型的方法是一种闭环的方法,它通过不断地修正SOC估计值,使得算法具有一定的鲁棒性。一般来说,基于模型的方法估计精度由预估过程与修正过程两部分共同决定,当信任安时积分的估计结果(SOC预估值较准)时,可适当地减小增益修正;否则应增大增益修正。但是过大的修正会使得SOC值波动剧烈,具体应该根据实际情况调整。
基于模型的估计方法的性能同时取决于模型与状态估计算法两者的性能。卡尔曼滤波(Kalman Filter,KF)类算法是动力电池SOC估计中使用最多的算法。KF是由美国学者Kalman在20世纪60年代初提出的一种最小方差意义上的最优估计方法。它提供了直接处理随机噪声干扰的解决方案,将参数误差看作噪声以及把预估计量作为空间状态变量,充分利用测量数据,用递推法将系统及随机测量噪声滤掉,得到准确的空间状态值。但是,最初的KF仅适用于线性系统,扩展卡尔曼滤波算法(Extended Kalman Filter,EKF)的提出使其推广到了非线性系统。EKF应用泰勒展开将动力电池模型线性化,但在线性化的过程中会带来截断误差,进而增大SOC估计误差,在某些初值设置不当的情况下甚至造成发散。为此,需要对动力电池模型进行改进和优化,或者使用改进后的卡尔曼滤波算法提高状态估计系统的精度和鲁棒性。尽管EKF尽量考虑了实际过程中的噪声,但其仍存在两点问题:
①它假设噪声不变,这显然与实际不符,而噪声信息协方差匹配算法的提出致力于解决这一问题,使得滤波算法中的噪声统计特性能随着估计结果的变化而自适应更新,如自适应扩展卡尔曼滤波(Adaptive
EKF,AEKF)。
②它假设噪声为白噪声,为了突破这一假设,人们使用基于最小化最大估计误差原则的H∞滤波(H∞
Filter,HIF)来完成动力电池的SOC估计,它承认实际过程中噪声统计特性未知,并基于此求得噪声统计特性使得估计结果最差时的状态估计最优解,保证最优状态估计。
4.基于数据驱动的方法
该方法指基于大量的离线数据,建立并训练动力电池电流、电压、温度等数据与动力电池SOC的直接映射关系模型。具体实现流程图如图4-3所示,主要分为3步:
①离线数据的预处理,即将数据整理为符合所建模型的输入输出要求的数据格式,包括数据清洗、归一化、数据分块等。其中数据分块指将归一化后的数据按照一定比例分为训练集、验证集与测试集。
②模型的建立与训练。根据数据量的大小,初步确定模型的结构,进而采用训练集训练所建模型,并以验证集验证结果为训练截止条件。
③模型的测试。采用测试集来测试模型,判断精度是否符合要求,若符合则判断训练完成;否则返回第①步重新进行设计与规划。

基于数据驱动的方法对解决强非线性问题有特别的优势,估计精度高,但是往往需要大量的实验数据作为先验知识,且所用实验数据应能充分反映动力电池特性;否则极易造成模型的过拟合。同时,所建模型的复杂度、所选训练函数与训练截止条件等也会直接影响模型的估计精度与泛化能力。
这类方法的典型代表是神经网络模型,该方法几乎不需要考虑动力电池的内部化学反应细节,同时它的拟合能力极强,理论上适用于任何种类动力电池的SOC估计。但是近年来,人们发现单一地增加神经网络的隐含层层数或单层神经元个数,会使得模型参数飞速增加,进而导致模型出现过拟合现象,因此神经网络的研究也逐渐转移到了泛化能力更强的深度学习网络上。同时,训练完成的神经网络模型结构较为复杂,计算量较大,在实车应用时往往需要高性能芯片,因此大量的神经网络/深度学习专用芯片也逐渐被投入市场。
四类方法的优缺点以及在精度与鲁棒性方面的表现见表。
四类SOC估计方法的优缺点及估计精度和鲁棒性的评价









 本文详细阐述了动力电池管理系统中关键的SOC和SOH估计方法,包括基于表征参数、安时积分、基于模型和数据驱动的四种常见策略。SOC作为电池的能量指示,精确估计对于电池管理至关重要。安时积分法简单实用但易受误差影响,基于模型的方法通过状态估计算法提高精度,而数据驱动方法则依赖大量实验数据。各种方法各有优劣,适用于不同应用场景。
本文详细阐述了动力电池管理系统中关键的SOC和SOH估计方法,包括基于表征参数、安时积分、基于模型和数据驱动的四种常见策略。SOC作为电池的能量指示,精确估计对于电池管理至关重要。安时积分法简单实用但易受误差影响,基于模型的方法通过状态估计算法提高精度,而数据驱动方法则依赖大量实验数据。各种方法各有优劣,适用于不同应用场景。
















 1733
1733

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








