剪枝+再训练：稀疏化DeepID2

本次介绍的依然是压缩网络的方法，不过有了具体的应用场景：压缩的模型是DeepID2+。方法来源于《2015 arxiv: Sparsifying Neural Network Connections for Face Recognition》，文章是王晓刚、汤晓鸥团队的，所以结果依旧很漂亮，但谁又能保证没点trick呢。T_T

压缩的核心：剪枝+再训练

算法流程

整个算法的流程很简单：从网络的最后一层开始，根据一定规则对该层进行剪枝，然后retrain网络，循环上述过程。

剪枝的实现方法，就是为权重施加一个相同大小的Mask, Mask中只有激活的地方才是1，其余全0.

算法流程图如下：

剪枝准则

剪枝的目标就是只保留重要的权重。

全连接层剪枝

首先，对于如全连接和局部连接这些没有权值共享的层，我们可以很简单的计算神经元之间的相关性：

假设  ai  是当前层的一个神经元， 上一层有  K  个神经元，则此时  ai  与上一层之间应该有  K  个连接，即  K  个权重参数：  bi1,bi2…biK 。 于是我们可以用下式计算  ai  与每一个  bik  的相关系数 ：

rik=E[ai−μai][bik−μbik]σaiσbik

其中  μ  和  σ  分别是在验证集上计算得到的均值与方差。

正相关和负相关同样重要，而且实验发现保留一些相关性较小的权重也会提高实验效果。

于是，作者首先将所有正相关的  rik  降序排列，然后均分为两部分，在前一部分随机采样  λSK+  个，在后面一部分随机采样  (1−λ)SK+  个, 其中  S  为事先确定的稀疏度，  λ 文中设定为0.75 。对负相关采取同样操作。据此，我们可以创建出表示剪枝的掩膜矩阵。

卷积层剪枝

卷积层剪枝稍微复杂一点，因为存在权值共享。

设  aim  是当前层第  i  个feature map中的第  m  神经元，该feature map中的共有  M  个神经元。显然，根据卷积规则，这  M  个神经元都只与一个卷积核有关，即  K  个权值有关 (  K  为filter size)。于是， (  bmk  应该是上一层 feature map 中卷积的部分，该部分的位置与  m  有关，且包含 (  K  个元素。

最后，相关系数通过平均的方式计算：

rik=∑m=1M∣∣∣E[aim−μaim][bmk−μbmk]σaimσbmk∣∣∣

实验分析

实验部分，主要是为了对比说明几处设置。

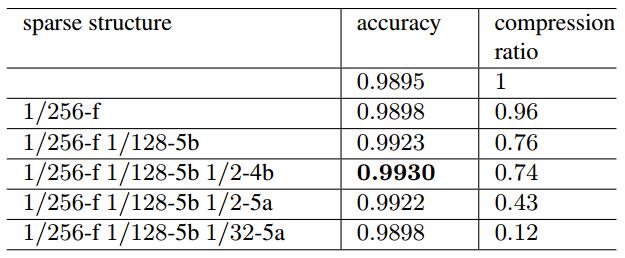
下面是在LFW人脸验证的实验，1/256表示稀疏度，整个实验都没有去碰卷积层，因为对于作者所用的VGG来说，全连接占据了90%的参数量。此外，压缩之后性能居然有提升，简直奇迹。

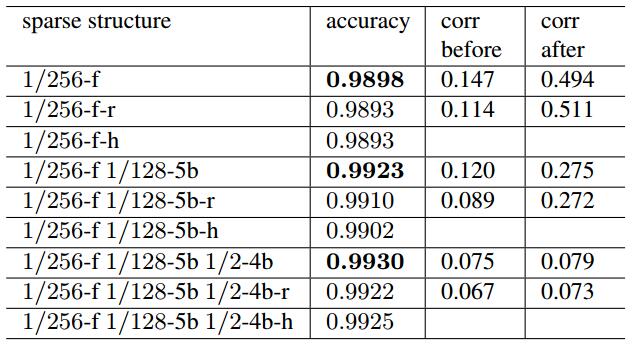
还记得之前选择权重的时候，是排序之后选择了一大部分相关性较高的加上一小部分相关性较小的。下图将其同另外两种策略进行了对比，一种是  r  表示全部随机选择，一种是 \(\h) 表示只选择相关性最高的。

结论就是：权重的幅值并不能很好地指示权重的重要性。

转自：http://blog.csdn.net/shuzfan/article/details/51700584