天津大学研究团队：基于黎曼几何的空间滤波方法显著提升运动想象脑电分类

脑机接口（BCI）技术近年来发展迅速，其中运动想象（Motor Imagery, MI）BCI 可让用户通过想象运动来控制外部设备，为残障康复和增强现实等领域带来巨大潜力。然而，MI-EEG信号非平稳、信噪比低，易受外界噪声和生理干扰，导致分类准确率难以提升。传统方法如常见共空间模式（CSP）假设数据平稳且服从高斯分布，在实际应用中往往表现欠佳。为此，研究人员提出了一种基于黎曼几何的空间滤波方法（Riemannian Spatial Filtering, RSF），通过将EEG信号投影到低维空间并最大化不同类别协方差矩阵间的黎曼距离，挖掘数据固有的几何结构。大量实验表明，RSF预处理能显著提高MI-EEG信号的分类准确率并缩短计算时间（尤其对深度学习模型），为构建鲁棒的MI-BCI系统提供了新思路。

01

研究背景

脑-机接口技术旨在将脑电等神经信号转化为计算机指令，实现大脑与外部设备的直接交互。其中，运动想象BCI通过让用户仅想象肢体运动即可进行交互控制，为脑卒中、脊髓损伤等患者提供了重获自主运动能力的希望。MI-BCI也可应用于虚拟现实、游戏等场景，改善健康人群的操控效率。在MI-BCI系统中，常用电生理信号是脑电（EEG），它具有高时域分辨率，但空间分辨率较差，且存在体积传导效应，使得神经信号在传递过程中发生扩散和衰减。此外，EEG信号容易受到环境噪声和肌电等生理干扰，给后续的信号处理和模式识别带来极大挑战。因此，对EEG信号进行有效的预处理和特征提取，对于提升MI-BCI系统的可靠性和精度至关重要。

为了应对上述挑战，研究人员提出了多种信号处理技术。其中，共空间模式（CSP）是一种经典的空间滤波算法，通过对两类信号的协方差矩阵进行特征分解，提取最大化类别间方差差异的投影。CSP简洁高效，在MI-BCI领域被广泛应用。然而，CSP存在明显局限：它假设EEG数据服从平稳高斯分布，在实际非平稳脑电环境下往往不成立；同时CSP对噪声非常敏感，特别是在训练样本量较小时，容易出现过拟合，稳健性和泛化能力有限。这些问题促使研究者探索更强健的空间滤波和特征提取方法。

近年来，引入黎曼几何理论为EEG信号处理提供了新的思路。黎曼几何方法将EEG样本表示为协方差矩阵所构成的对称正定（SPD）流形，并采用非欧几里得度量来分析这些矩阵。相较于传统欧式方法，黎曼方法具有明显优势：它能够捕捉EEG信号的空间相关性，对体积传导效应具有相对不变性；在流形上进行白化和对齐操作可以提高算法在不同被试或任务间的可移植性。更重要的是，黎曼距离度量对噪声具有更好的鲁棒性，有效减少环境和生理噪声对分类的影响。基于黎曼流形的分类算法（如最小距离均值MDM、切空间映射TSM等）在MI-EEG处理中取得了显著成果。然而，现有研究主要关注分类器设计，利用黎曼流形进行空间滤波（相当于学习投影矩阵）方面的研究仍然较少。高维度和非线性的MI-EEG特征使得提取判别信息更加困难，同时对于实时和资源受限场景下的计算效率也提出了要求。为此，本研究提出了一种新的黎曼流形空间滤波方法RSF（Riemannian Spatial Filtering），期望结合黎曼几何优势，通过滤波和降维在保持信号判别信息的同时减轻计算负担，从而提高MI-BCI的性能。

02

研究概述

本研究针对MI-EEG分类中的空间滤波需求，设计了RSF方法。该方法的核心思想是：在黎曼流形上直接学习一个线性投影矩阵，将原始EEG多通道信号映射到低维空间，使得不同类别的协方差矩阵在黎曼度量下的距离最大。具体来说，研究团队首先为每个试验计算协方差矩阵，并分别计算两类样本的黎曼几何平均协方差矩阵。接着，定义了一个目标函数，该函数衡量在投影后两类平均协方差矩阵之间的黎曼距离，如下式所示：

由于黎曼距离具有仿射不变性，RSF可有效降低信号维度而不丢失重要信息。为了求解该优化问题，研究人员采用了BFGS算法进行迭代优化。在每次迭代中，通过计算梯度和采用线性搜索调整步长，滤波矩阵不断更新，直到目标函数在训练和测试集上均收敛稳定。主要数据处理的流程如图1所示：

图1 数据处理流程图（图片来自原文）

在实验设计上，研究团队使用了六个公开MI-BCI数据集，覆盖左右手想象等任务，总计265名被试（表1）。实验采用被试内的10折交叉验证，对比条件包括无空间滤波、CSP滤波和RSF滤波三种。此外，研究纳入了十种常用解码算法进行评估，包括传统机器学习方法（CSP-LDA、FBCSP、MDM、TSM）和多种深度学习模型（EEGNet、sCNN、dCNN、FBCNet、Graph-CSPNet、LMDA-Net）。CSP和RSF的投影维度均设为8维，深度学习模型采用Adam优化器训练。

实验结果显示，RSF显著改善了MI-EEG分类性能。如图2所示，RSF预处理后的各算法准确率均高于无滤波基线点（所有算法差异均通过统计检验，p<0.001）。例如，在不使用滤波的情况下，最优基线算法TSM平均准确率为65.9%；而在RSF处理中，RSF-FBCNet和RSF-Graph-CSPNet分别达到68.8%的平均准确率，领先无滤波和CSP方案。进一步地，与传统CSP比较（图3），RSF在多数算法上效果更佳：TSM、EEGNet、sCNN、FBCNet和Graph-CSPNet等算法使用RSF后准确率显著提升（p<0.001）。仅有MDM和LMDA-Net等个别算法在CSP滤波下略优于RSF，说明RSF并非对所有模型都呈现压倒性优势，但总体效果可观。综合来看，RSF增强后的算法在几乎所有数据集上均获得了最高或第二高的分类准确率，验证了其广泛适用性。

图2 使用RSF空间滤波（w/ RSF）与不使用RSF空间滤波（w/o RSF）时，十种常见算法的分类准确率对比（图片来自原文）

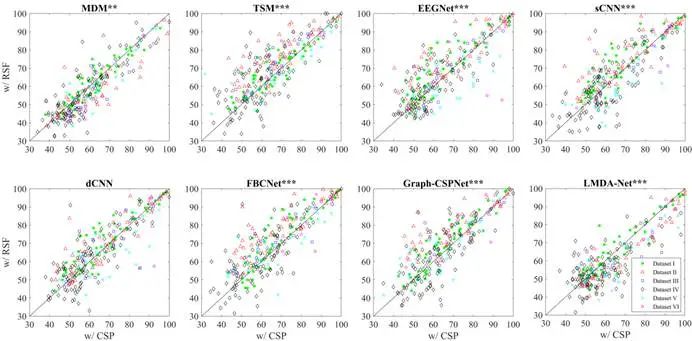
图3 使用RSF空间滤波（w/ RSF）与使用CSP空间滤波（w/ CSP）时，八种常见算法的分类准确率对比（图片来自原文）

从特征可分性角度分析，RSF同样表现出优越性。图4展示了三种条件下两类平均协方差矩阵及其对数差异，结果显示RSF后的矩阵在Frobenius范数上比CSP略大，意味着RSF保留了更多类间可辨信息。而t-SNE可视化（见图5）更直观地展示了样本分布：RSF滤波后两类样本聚类更加明显，Fisher判别分数也显著高于CSP处理。这些结果表明，RSF通过利用协方差空间的几何特性，有效地增强了类别间差异。

图4 三种不同空间滤波情形下，两类样本的平均协方差矩阵及其对数差异（图片来自原文）

图5 六个公开数据集的一名受试者在三种不同空间滤波情形下，两类样本的t-SNE分布（图片来自原文）

在计算效率方面，RSF对大多数模型的训练时间影响很小，但对复杂网络有显著改善。研究表明，对于Graph-CSPNet等对输入维度敏感的模型，RSF降维后训练时间大幅减少，有时可节省数小时。图6中随着RSF滤波维度d的增加，训练时间呈指数增长趋势：在d=4–8时，训练时间相对较低，而d=16时训练时间急剧增加。这提示实践应用中应在性能提升和计算成本之间权衡，选取中等维度即可获得最佳效果。

图6 三种主要算法在不同空间滤波器维度的训练时间成本（图片来自原文）

03

主要创新点

本研究的主要创新点和贡献包括：

• 提出了一种新的基于黎曼流形的空间滤波方法RSF，用于MI-EEG信号降维和去噪，填补了MI-BCI在黎曼几何空间滤波技术领域的空白。

• 对RSF进行了系统评估，结合十种不同的解码算法进行大规模比较实验，结果表明RSF能显著增强各种类型算法的分类性能。

• 分析了不同滤波维度对分类性能的影响，为实际中选择合适的滤波维度提供了经验指导（多数情况下在6–12维时性能最佳，超出范围收益有限）。

04

研究意义

该工作展示了简洁高效的黎曼空间滤波方法在MI-BCI中的潜力。通过RSF预处理，多种MI-EEG解码算法的分类准确率显著提升，特别是在深度学习模型上的增益明显；同时，RSF方法对于不同类型和规模的数据表现出了良好的稳健性和适应性。这意味着，RSF技术可作为MI-BCI系统的通用预处理工具，提升神经信号解码的可靠性和精度。研究结果凸显了RSF方法在提升MI-BCI系统性能方面的关键价值，为脑电信号处理领域提供了新的思路与手段。

展望未来，RSF方法具有进一步扩展的可能性。研究团队指出，可将RSF应用于迁移学习和领域适应等场景，帮助模型在不同任务或个体间更好地泛化。同时，可继续优化RSF算法本身，例如改进滤波维度选择策略和计算效率，以适应更多样化的数据和实时应用需求。在这些努力下，RSF有望对神经科学和工程研究产生深远影响，为脑机接口技术的实际落地和推广提供有力支撑。

参考文献：

Lincong Pan, Kun Wang, Yongzhi Huang, et al. Enhancing motor imagery EEG classification with a Riemannian geometry-based spatial filtering (RSF) method[J]. Neural Networks, 2025, 188: 107511, doi: 10.1016/j.neunet.2025.107511.

论文临时链接（ Anyone clicking on this link before June 16, 2025 will be taken directly to the final version of your article on ScienceDirect, which they are welcome to read or download. No sign up, registration or fees are required.）：

https://authors.elsevier.com/c/1k-U43BBjKvXU5

代码下载链接：

https://github.com/PLC-TJU/RSF

仅用于学术分享，若侵权请留言，即时删侵！

   加入社群   

欢迎加入脑机接口社区交流群，

探讨脑机接口领域话题，实时跟踪脑机接口前沿。

加微信群：

添加微信:RoseBCI【备注：姓名+行业/专业】。

加QQ群：913607986

   欢迎来稿   

1.欢迎来稿。投稿咨询，请联系微信：RoseBCI

点击投稿：脑机接口社区学术新闻投稿指南

2.加入社区成为兼职创作者，请联系微信：RoseBCI

一键三连「分享」、「点赞」和「在看」

不错过每一条脑机前沿进展