蓝桥杯备赛（基础语法1）

·时间复杂度

时间复杂度

1)时间复杂度是衡量算法执行时间随输入规模增长的增长率。

2)通过分析算法中基本操作的执行次数来确定时间复杂度。
3)常见的时间复杂度包括 : 常数时间O(1)、线性时间O(n)、对数时间O(log n)、平方时间
   O(n^2)等。
4)在计算的时候我们关注的是复杂度的数量级，并不要求严格的表达式。
一般我们关注的是最坏时间复杂度，用O(f(n)表示，大多数时候我们仅需估算即可。
一般来说，评测机1秒大约可以跑2e8次运算，我们要尽可能地让我们的程序运算规模数量级控制在1e8以内。

空间复杂度

1)空间复杂度是衡量算法执行过程中所需的存储空间随输入规模增长的增长率。

2)通过分析算法中所使用的额外存储空间的大小来确定空间复杂度。
3)常见的空间复杂度包括：常数空间O(1)、线性空间O(n)、对数空间O(logn)、平方空间
 O(n^2)等。
一般我们关注的是最坏空间复杂度，用O(f(n)表示，大多数时候程序占用的空间一般可以根据开的数组大小精确算出，但也存在需要估算的情况。题目一般不会卡空间，一般是卡时间。举个例子，假如题目限制128MB,1int~32bit~4Bytes,128MB~32*2^20int~3e7int

分析技巧

1.理解基本操作：基本操作可以是算术运算（加法、乘法、位运算等）、比较操作、赋值操作等。
2.关注循环结构：循环是算法中常见的结构，它的执行次数对于时间复杂度的分析至关重要。
3.递归算法：递归算法的时间和空间复杂度分析相对复杂。需要确定递归的深度以及每个递归调用的时间和空间开销。
4.最坏情况分析：对于时间复杂度的分析，通常考虑最坏情况下的执行时间。要考虑输入数据使得算法执行时间达到最大值的情况。
5.善用结论：某些常见算法的时间和空间复杂度已经被广泛研究和证明。可以利用这些已知结果来分析算法的复杂度。

代码示例

(1)

时间复杂度：O(n)
该算法通过循环遍历数组中的每个元素，并对它们求和，因此时间复杂度与数组中的元素数量成正比。
 空间复杂度：O(n)
因为开了一个大小为n的vecter,算法使用了一个大小为n的向量来存储输入元素，所以空间复杂度与输入元素的数量成正比

该代码时间复杂度是O（n) , O(2n) = O(n),因为关注的是复杂度的数量级,例如O(n^2 + nlogn + n) = O(n^2);

(2)

时间复杂度；O(n)
该算法使用迭代的方式计算斐波那契数列的第n个数，循环遍历n次，因此时间复杂度与n成正比。
空间复杂度：O(1)
算法只使用了常数级别的额外空间来存储变量，不随输入规模变化。

(3)

(4)

·枚举

枚举算法介绍

枚举算法是一种基本的算法思想，它通过穷举所有可能的情况来解决问题。它的基本思想是将问题的解空间中的每个可能的解都枚举出来，并进行验证和比较，找到满足问题条件的最优解或者所有解。
枚举算法适用于问题规模较小、解空间可穷举的情况。它的优点是简单直观，不需要复杂的数学推导，易于实现。但是，由于需要穷举所有可能的情况，对于问题规模较大的情况，枚举算法的时间复杂度可能会非常高，效率较低。

解空间类型

解空间可以是一个范围内的所有数字（或二元组、字符串等数据），或者满足某个条件的所有数字。
当然也可以是解空间树，一般可分为子集树和排列树，针对解空间树，需要使用回溯法进行枚举
我们目前仅使用循环去暴力枚举解空间，具体的解空间类型需要根据题目来理解构造。

循环枚举解空间

1.首先确定解空间的维度，即问题中需要枚举的变量个数。
例如当题目要求的是满足条件的数字时，我们可以循环枚举某个范围内的数字。
如果要求的是满足条件的二元组，我们可以用双重循环分别枚举第一个和第二个变量，从而构造出一个二元组。
2.对于每个变量，确定其可能的取值范围。这些范围可以根据问题的性质和约束条件来确定。这一步往往是时间复杂度优化的关键。
3.在循环体内，针对每个可能解进行处理。可以进行问题的验证、计算、输出等操作。

例题讲解

（1）

（2）

（3）

·模拟

模拟算法介绍

模拟算法通过模拟实际情况来解决问题，一般容易理解但是实现起来比较复杂，有很多需要注意的细节，或者是一些所谓很“麻烦”的东西。
模拟题一般不涉及太难的算法，一般就是由较多的简单但是不好处理的部分组成的，考察选手的细心程度和整体的逻辑思维。
一般为了使得模拟题写的逻辑清晰一些，经常会写比较多的小函数来帮助解题，例如int和string的相互转换、回文串的判断、日期的转换、各种特殊条件的判断等等。

例题讲解

（1）

（2）

（3）

·进制转换

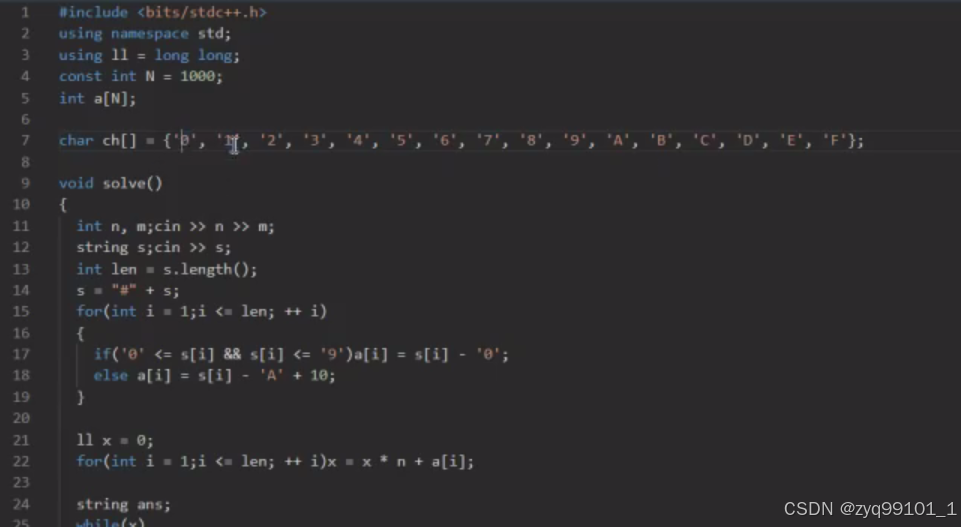
将任意进制转换为十进制

假设给了一个数组来表示一个k进制（假设k >10）的整数，我们该如何得到它的十进制数

i = 1, x = 1 * k ^ 0;

i = 2, x = 1 * k ^ 1 + 3 * k ^ 0;

i = 3, x = 1 * k ^ 2 + 3 * k ^ 1 + 10 * k ^ 0;

······

i = 5, x = 1 * k ^ 4 + 3 * k ^ 3 + 10 * k ^ 2 + 5 * k ^ 1 + 7 * k ^ 0;

·将十进制转换为任意进制

假设现在有一个十进制数x,如何转换为k进制呢？

我们可以先假设一个x的k进制表达式，再逐步地去求解。

x=an × k ^ n + ... + a1 × k ^ 1 + a0 × k ^ 0

对于这个表达式,我们可以快速计算出a0 =x % k
计算出a0之后怎么办，我们只需要将 x /= k,就可以将原本的a1放到a0位置上，再同样求解即可。
 

x / k = an × k ^ (n-1) + ... + a1 × k0

例题讲解

（1）

（2）

（3）