模式识别—实验六：高维数据的低维可视化

zyx1111111111

于 2025-03-18 21:26:52 发布

阅读量611

点赞数 15

分类专栏：模式识别作业文章标签：人工智能 python 算法

本文链接：https://blog.csdn.net/zyx302626/article/details/146352516

版权

模式识别作业专栏收录该内容

7 篇文章

订阅专栏

一、实验任务（后附完整代码）

问题描述：

瑞士卷数据集是一个常用于降维和可视化算法测试的数据集，其中包含了一个三维曲面，其形状类似于卷曲的纸卷或薄蛋糕。这个数据集常被用来模拟具有复杂非线性结构的数据，以便研究降维方法在处理高维数据时的性能。

本实验使用PCA、MDS、IsoMap和t-SNE方法对瑞士卷数据集进行降维可视化，以探索这些算法在捕捉数据内在结构和可视化复杂数据时的性能差异。

2. 实验内容：

生成瑞士卷数据，并进行可视化显示；
降维可视化：分别使用PCA、MDS、IsoMap和t-SNE方法将瑞士卷数据集可视化成二维图形，其中PCA方法需要手动编程实现，其他方法均可调包实现；
t-SNE的参数分析：比较不同迭代次数对t-SNE可视化结果的影响。
不同方法的比较：比较线性方法和非线性方法以及不同非线性方法之间的可视化结果，并对结果进行解释说明；

二、算法原理概述

主成分分析（Principal Component Analysis,PCA）是一种常见的数据分析方式，常用于高维数据的降维，可用于提取数据的主要特征分量。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。

PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0，可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴，实现对数据特征的降维处理。

PCA 的算法步骤：

设有 m 条 n 维数据。

将原始数据按列组成 n 行 m 列矩阵 X；
将 X 的每一行进行零均值化，即减去这一行的均值;
求出协方差矩阵
求出协方差矩阵的特征值及对应的特征向量；
将特征向量按对应特征值大小从上到下按行排列成矩阵，取前 k 行组成矩阵 P；
即为降维到 k 维后的数据。

2. MDS

多维尺度变换(multidimensional scaling, MDS)是在低维空间去展示高维多元数据的一种可视化方法。将定义在多维空间中的样本间的关系按比例缩放到二维或三维空间中显示出来。基本出发点为：并不是把样本从一个空间映射到另一个空间，而是把样本之间的距离关系或不相似度关系在低维空间（如二维或三维空间）里表示出来。类型分为度量型（定量度量：保持度量关系）和非度量型（定性关系：保持顺序）。在度量型MDS中，依据度量的距离标准是否是欧氏距离，分为经典多维尺度变换(classical MDS)和非经典多维尺度变换(non-classical MDS)。

在classical MDS中，通过高维空间中的距离矩阵，求解在低维空间中的坐标的推导步骤如下所示：

Classical MDS 算法流程：

计算原始空间中数据点的距离矩阵。
计算内积矩阵 B。
对矩阵B进行特征值分解，获得特征值矩阵和特征向量矩阵。
取特征值矩阵最大的前k项及其对应的特征向量。

3. IsoMap

IsoMap算法是基于前面所讲的MDS算法，不同之处在于isomap用图中两点的最短路径距离替代了MDS中欧式空间的距离，这样能更好的拟合流行体数据。

流形的概念：在点所在的高维空间中的一个低维子空间，在这个低维子空间中，点之间的关系如同

在低维的欧氏空间中一样。在数学上，流形用于描述一个几何形体，它在局部具有欧氏空间的性质。即可用欧氏距离来描述局部区域，但在全局欧氏距离不成立。下图展示了在“瑞士卷”流形上的情况：

IsoMap算法流程：

设置每个点最近邻点数k,构建连通图和邻接矩阵。
通过图的最短路径构建原始空间中的距离矩阵。
计算内积矩阵B。
对矩阵B进行特征值分解，获得特征值矩阵和特征向量矩阵。
取特征值矩阵最大的前k 项及其对应的特征向量。

4. t-SNE

t分布随机近邻嵌入法(t-distributed stochastic neighbor embedding,t-SNE)是用于降维的一种机器学习算法，是由 Laurens van der Maaten 和 Geoffrey Hinton在08年提出来。此外，t-SNE 是一种非线性降维算法，非常适用于高维数据降维到2维或者3维，进行可视化。

本质是基于流形学习（manifold learning）的降维方法，即寻找高维数据中可能存在的低维流形。在SNE方法的基础上发展而来，利用概率分布来度量样本间的距离，将高维空间中的欧式距离转化为条件概率密度函数来表示样本间的相似度。特点是能够保持样本间的局部结构，使得在高维数据中距离相近的点投影到低维中仍然相近，常用作样本可视化分析。

t-SNE方法的步骤如下：

三、测试步骤

运行文件，mnist数据集位置“./代码/data”，输出如下：

瑞士卷数据的可视化显示；
PCA的降维可视化结果；
MDS的降维可视化结果；
IsoMap的降维可视化结果；
不同迭代次数下t-SNE的降维可视化结果；
补充：利用IsoMap对mnist数据集进行降维的结果；

四、实验结果与讨论

实验结果：

瑞士卷数据的可视化显示；

PCA的降维可视化结果；

比较sklearn中的pca和自己编写的pca的区别：

MDS的降维可视化结果；

IsoMap的降维可视化结果；

不同迭代次数下t-SNE的降维可视化结果；

补充：利用IsoMap对mnist数据集进行降维的结果；
mnist数据集下载在文章上方。

结果分析：

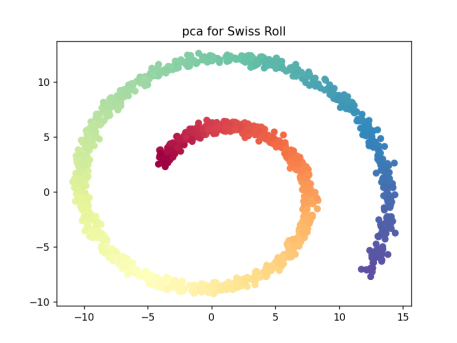
使用pca对瑞士卷进行降维：从结果中可以看到由于pca是线性的降维方法，在处理瑞士卷这样的非线性问题时，得到的效果并不好，pca投影得到的两个主成分沿着流形的颜色重叠混合。
使用MDS对瑞士卷进行降维：MDS虽然为非线性降维，但使用欧式距离作为度量，由于欧氏距离在流形上全局不成立，在处理高维的流形时，同样降维的效果不好，投影得到的结果是一个卷的形状。
使用IsoMap对瑞士卷进行降维：IsoMap使用两个样本间最短路径的局部距离之和作为两个样本间的距离（测地距离）作为度量，再映射到低维空间，得到了一个瑞士卷近似展开平铺的效果。
使用t-SNE对瑞士卷进行降维，并比较不同迭代次数下降维的效果：利用概率分布来度量样本间的距离，将高维空间中的欧式距离转化为条件概率密度函数来表示样本间的相似度，保持了样本间的局部结构，使得在高维数据中距离相近的点投影到低维中仍然相近。故结果呈现近似簇的效果。同时随着迭代次数的增加，得到的结果中相同的类之间越紧凑。
使用IsoMap对mnist进行降维：将mnist数据集从784维降维到2维，绘制出前两个主成分的降维结果，可以看到相同数字聚集成簇，不同数字间相对区分，仅使用前两个主成分有一定的区分效果。

综上，在处理瑞士卷数据集的问题上，由于瑞士卷数据集是非线性流形，线性降维方法PCA和以欧式距离为度量的非线性降维方法MDS处理效果并不好，使用测地距离作为度量的IsoMap和利用概率分布来度量样本间的距离的t-SNE方法则相对效果较好，其中IsoMap得到的结果是将瑞士卷展平铺开，t-SNE的结果则使相同类别的样本局部结构不变。

以下为在官网上找到的各种降维方法的效果图，与本次的实验结果较为相似，但样本数量上有区别：

五、实验总结(总结本次实验课学习的内容、结论、反思 )

在本次实验中我们主要掌握了主成分分析（Principal Component Analysis，PCA）、多维尺度变换（Multidimensional Scaling，MDS）、等距特征映射（Isometric Mapping，IsoMap）和t分布式随机邻居嵌入（t-distributed Stochastic Neighbor Embedding，t-SNE）四种降维方法的的基本原理，并使用了PCA、MDS、IsoMap和t-SNE方法对瑞士卷数据集进行降维可视化，以探索这些算法在捕捉数据内在结构和可视化复杂数据时的性能差异。以及比较了线性方法（PCA）和非线性方法以及不同非线性方法（MDS、IsoMap、t-SNE）之间的可视化结果的不同。

其中得到的结论有：

PCA线性降维方法：从结果中可以看到由于pca是线性的降维方法，在处理瑞士卷这样的非线性问题时，得到的效果并不好，pca投影得到的两个主成分沿着流形的颜色重叠混合。
MDS使用欧式距离作为度量的非线性降维方法：对瑞士卷进行降维时，由于欧氏距离在流形上全局不成立，在处理高维的流形时，同样降维的效果不好，投影得到的结果是一个卷的形状。
IsoMap使用最短测地路径度量的非线性降维方法：在处理流形的降维问题上效果较好，对瑞士卷进行降维：IsoMap使用两个样本间最短路径的局部距离之和作为两个样本间的距离（测地距离）作为度量，再映射到低维空间，得到了一个瑞士卷近似展开平铺的效果。
t-SNE利用概率分布来度量样本间的距离的非线性降维方法：对瑞士卷进行降维时，利用概率分布来度量样本间的距离，将高维空间中的欧式距离转化为条件概率密度函数来表示样本间的相似度，保持了样本间的局部结构，使得在高维数据中距离相近的点投影到低维中仍然相近，故结果呈现近似簇的效果。同时随着迭代次数的增加，得到的结果越紧凑。

遇到的问题：

三维图的绘制

在普通绘图的代码上添加projection=‘3d’

fig=plt.figure(1)

ax = fig.add_subplot(111, projection='3d')

ax.scatter(data[:,0],data[:,1],data[:,2],c=color,cmap=plt.cm.Spectral)

plt.title("Swiss Roll")

PCA标准化

使用自己编写的PCA代码时，得到的错误结果如下：

检查后发现是没有对数据进行去均值去方差的标准化造成的，增加下面的代码后正常：

mean = np.mean(data, axis=0)

std = np.std(data, axis=0)

normalized_data = (data - mean) / std

中心化的目的是消除原始数据不同维度上的特征的尺度（单位）上的不一致，利用标准化步骤对数据进行预处理。

噪声造成降维效果不好

当生成的瑞士卷数据集噪声为1时，不论怎样调节isoMap的参数如n_neighbers，得到的降维效果始终不好，如下图所示：

data,color=make_swiss_roll(n_samples=1500,noise=1,random_state=42)

后将噪声修改为0.25时，得到了较好的类似于铺开的降维效果。

data,color=make_swiss_roll(n_samples=1500,noise=0.25,random_state=42)

绘制IsoMap降维mnist的结果时，想得到相同数字聚集成簇的效果，故想找到0-9的数字型maker，但在常用的maker里面没有。因此上网找到了自定义maker的方法。

for i in range(10):

plt.scatter(X_transformed[label == i, 0], X_transformed[label == i, 1],marker='$'+str(i)+'$')

最终结果如下：

python代码：

from sklearn.datasets import make_swiss_roll
from sklearn.manifold import MDS,Isomap,TSNE
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
import numpy as np
from struct import unpack
# 取消注释即可运行
# def pca(X, n_components=None):     #自定义的pca函数
#     # 计算数据的协方差矩阵
#     cov_matrix = np.cov(X, rowvar=False)
#
#     # 计算协方差矩阵的特征值和特征向量
#     eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
#
#     # 对特征值进行排序
#     sorted_indices = np.argsort(eigenvalues)[::-1]  # 降序排列
#     eigenvalues = eigenvalues[sorted_indices]
#     eigenvectors = eigenvectors[:, sorted_indices]
#
#     if n_components is None:
#         n_components = X.shape[1]
#
#     # 选取前n_components个特征向量
#     top_eigenvectors = eigenvectors[:, :n_components]
#
#     # 项目数据到新的特征空间
#     reduced_data = np.dot(X, top_eigenvectors)
#
#     return reduced_data
# #生成瑞士卷数据集
# data,color=make_swiss_roll(n_samples=1500,noise=0.25,random_state=42)
#
# #绘制瑞士卷数据集
# fig=plt.figure(1)
# ax = fig.add_subplot(111, projection='3d')
# ax.scatter(data[:,0],data[:,1],data[:,2],c=color,cmap=plt.cm.Spectral)
# plt.title("Swiss Roll")
#
# #使用pca进行降维的结果
# plt.figure(2)
# # 预处理标准化很关键
# mean = np.mean(data, axis=0)
# std = np.std(data, axis=0)
# normalized_data = (data - mean) / std
# pcaa=PCA(n_components=2)   #调用sklearn包里的pca函数
# pca_data1=pcaa.fit_transform(normalized_data)
# pca_data2=pca(normalized_data,n_components=2) #调用自己编写的pca函数
# plt.suptitle("pca for Swiss Roll")
# plt.subplot(121)
# plt.title("sklearn pca ")
# plt.scatter(pca_data1[:,0],pca_data1[:,1],c=color,cmap=plt.cm.Spectral)
# plt.subplot(122)
# plt.title("my pca ")
# plt.scatter(pca_data2[:,0],pca_data2[:,1],c=color,cmap=plt.cm.Spectral)
#
#
# #使用mds进行降维的结果
# plt.figure(3)
# mds = MDS(n_components=2,dissimilarity='euclidean')
# mds_data=mds.fit_transform(data)
# plt.title("MDS for Swiss Roll")
# plt.scatter(mds_data[:,0],mds_data[:,1],c=color,cmap=plt.cm.Spectral)
#
#
# #使用IsoMap进行降维的结果
# plt.figure(4)
# isomap=Isomap(n_components=2,n_neighbors=15)
# isomap_data=isomap.fit_transform(data)
# plt.title("isomap for Swiss Roll")
# plt.scatter(isomap_data[:,0],isomap_data[:,1],c=color,cmap=plt.cm.Spectral)
#
#
# #使用t-SNE进行降维并比较不同的迭代次数的结果
# plt.figure(5)
# n_iter=np.array([500,1000,1500,2000,3000])
# num=1
# plt.suptitle("tsne for Swiss Roll")
# for i in n_iter:
#     tsne=TSNE(n_components=2,n_iter=i)
#     tsne.fit(data)
#     tsne_data=tsne.fit_transform(data)
#     plt.subplot(1,n_iter.shape[0],num)
#     plt.scatter(tsne_data[:,0],tsne_data[:,1],c=color,cmap=plt.cm.Spectral)
#     plt.title("iter={}".format(i))
#     num+=1
#
#
# plt.show()


# 尝试对mnist数据集进行降维
def readimage(path):       # 读取数据集
    with open(path, 'rb') as f:
        magic, num, rows, cols = unpack('>4I', f.read(16))
        img = np.fromfile(f, dtype=np.uint8).reshape(num, 784)
    return img


def readlabel(path):      # 读取数据集标签
    with open(path, 'rb') as f:
        magic, num = unpack('>2I', f.read(8))
        lab = np.fromfile(f, dtype=np.uint8)
    return lab

train_data = readimage("./data/train-images-idx3-ubyte")    #读取数据
train_label = readlabel("./data/train-labels-idx1-ubyte")


data=train_data[:900,:]
label=train_label[:900]


embedding = Isomap(n_components=2)
X_transformed = embedding.fit_transform(data)

plt.figure(6)
plt.title("isomap for mnist")
# plt.scatter(X_transformed[:,0],X_transformed[:,1],marker=["0","1","2","3","4","5","6","7","8","9"])
for i in range(10):
    plt.scatter(X_transformed[label == i, 0], X_transformed[label == i, 1],marker='$'+str(i)+'$')
plt.show()