t检验比较两种算法的性能

 

1.t检验理论

t-检验，又称学生检验，可以用于比较两组数据是否来自同一分布（可以用于比较两组数据的区分度），假设了数据的正态性，并反应两组数据的均值在统计上是否有显著差异。

2.实例分析

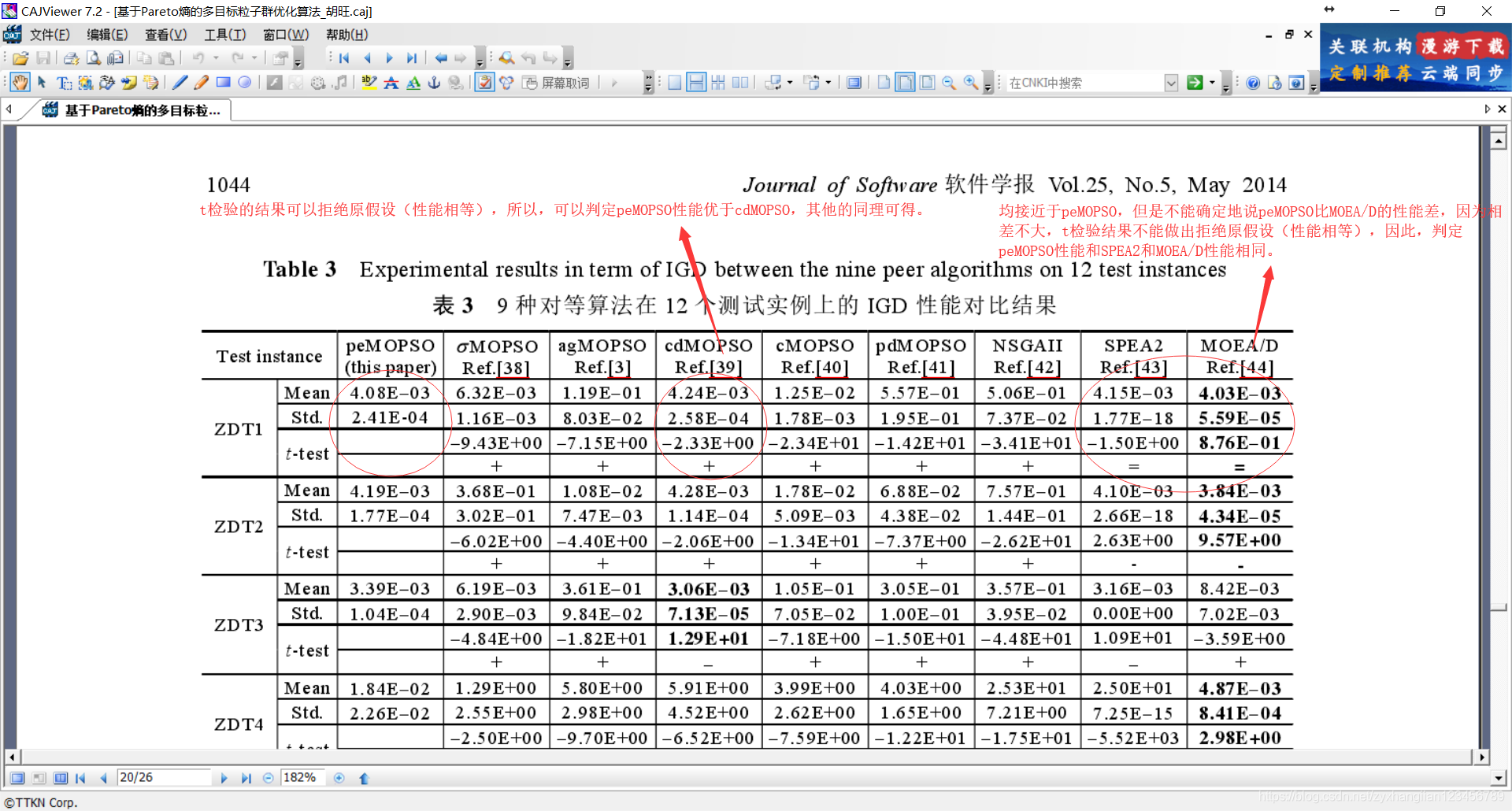
上面论文中，算法运行了30次，对于IGD指标来说，我们认为其值越小越好，如表所示，第一行中peMOPSO算法运行30次IGD指标的均值为4.08E-03，SPEA2算法运行30次IGD指标的均值为4.15E-03，MOEA/D算法运行30次IGD指标的均值为4.03E-03。是否可以说peMOPSO算法就优于SPEA2算法？又是否可以说peMOPSO算法劣于MOEA/D算法呢？

在统计学理论中，比较两个算法IGD指标优劣这个问题就归结为两个样本是否来自同一总体这一新问题。为了确定两个算法针对于某一问题的性能相对优劣，实际上需要做的就是，先假设他们之间的性能相同，即两个样本来自于同一个总体。接着，利用t检验代入t检验统计量，根据计算结果，判断是否能够推翻原假设。

当然，这种方法倾向于认为原假设成功，即只有在不得不拒绝原假设的情况下，才会去拒绝原假设，接受备选假设。

对于上述问题可以进行两个不同的假设。

假设1

H0：peMOPSO算法性能和SPEA2算法性能相同；

H1：peMOPSO算法优于SPEA2算法。

假设2

H0：peMOPSO算法性能和MOEA/D算法性能相同；

H1：peMOPSO算法劣于MOEA/D算法。

接着，进行t检验，验证假设是否成立。

3.Matlab下t检验方法

[h,p,ci]=ttest2(x,y，alpah);

其中，x,y均为行向量（维度必须相同），各表示一组数据，alpha为可选参数，表示设置一个值作为t检验执行的显著性水平。在不设置alpha的情况下，默认alpha为0.05，即计算x和y在5%的显著性水平下是否来自同一分布（假设是否被接受）。

h=0,则表明原假设在置信度下不被接受，即算法性能相差不大；h=1，表明原假设被拒绝，即均值差别很大，直接比较均值大小就可以了。

由于论文中实际的数据未知，因此，不再进行仿真实验。

文中部分内容参考了如下博文：

T检验

Matlab进行t检验

MATLAB ttest和ttest2的区别

ttest__t检验及matlab简析

简单理解t检验与秩和检验