本系列文章力求以简洁易懂的文字介绍计算几何中的基本概念,使读者快速入门,故不追求难度和深度,仅起到抛砖引玉的作用。

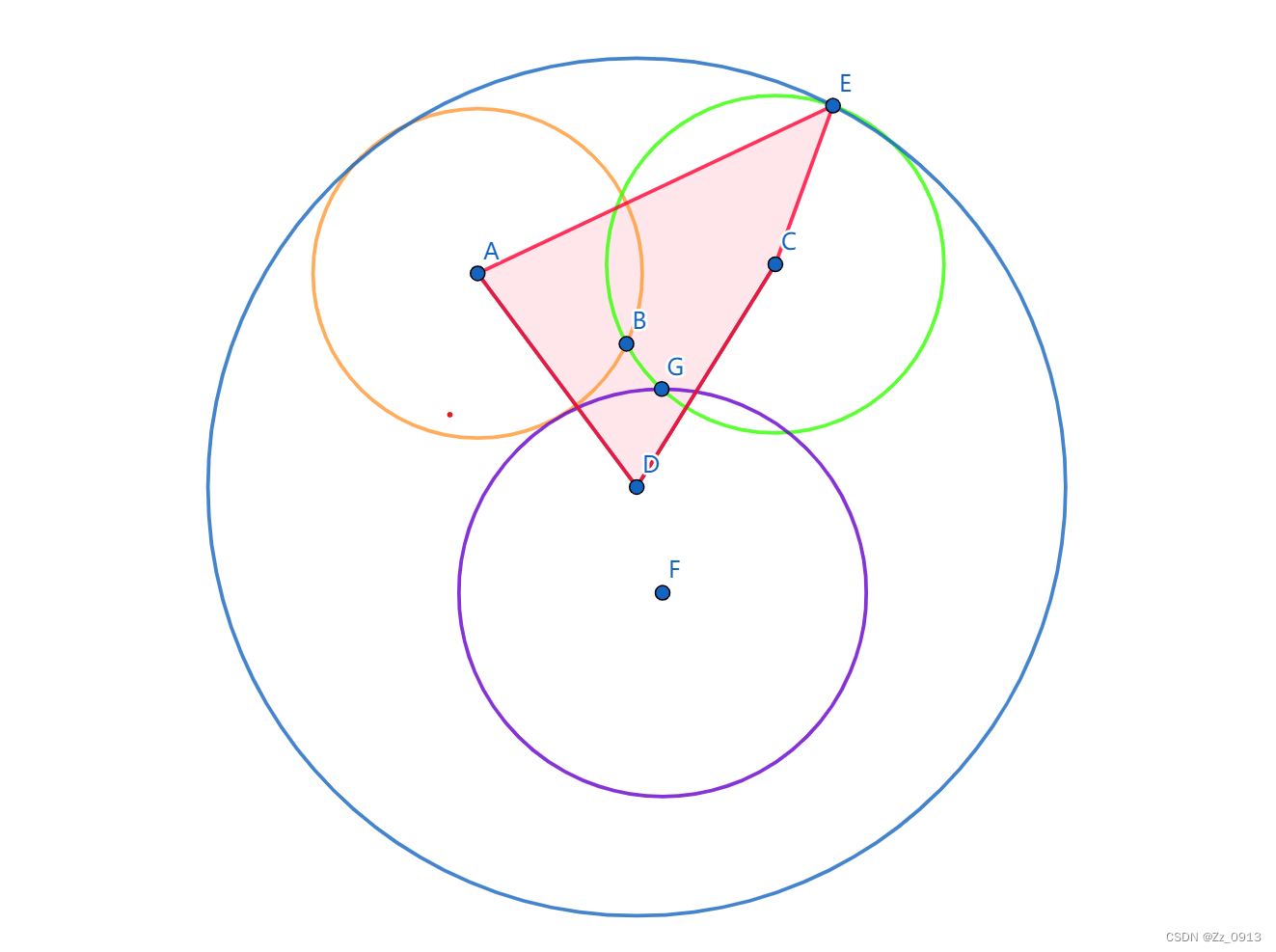
经过了一定的计算几何入门学习,我们已经成功掌握了计算几何基础操作和计算几何基础类型——也就是计算几何点类,线类,三角形类,多边形类。今天我们单独开一节文来讲解一下二维计算几何的圆类~
圆的结构体表示:Circle,包含一个Point类型和一个double类型,分别表示圆心的点和半径~(后面一段是求三角形的外接圆,圆定义方法,其实外心公式也可以):
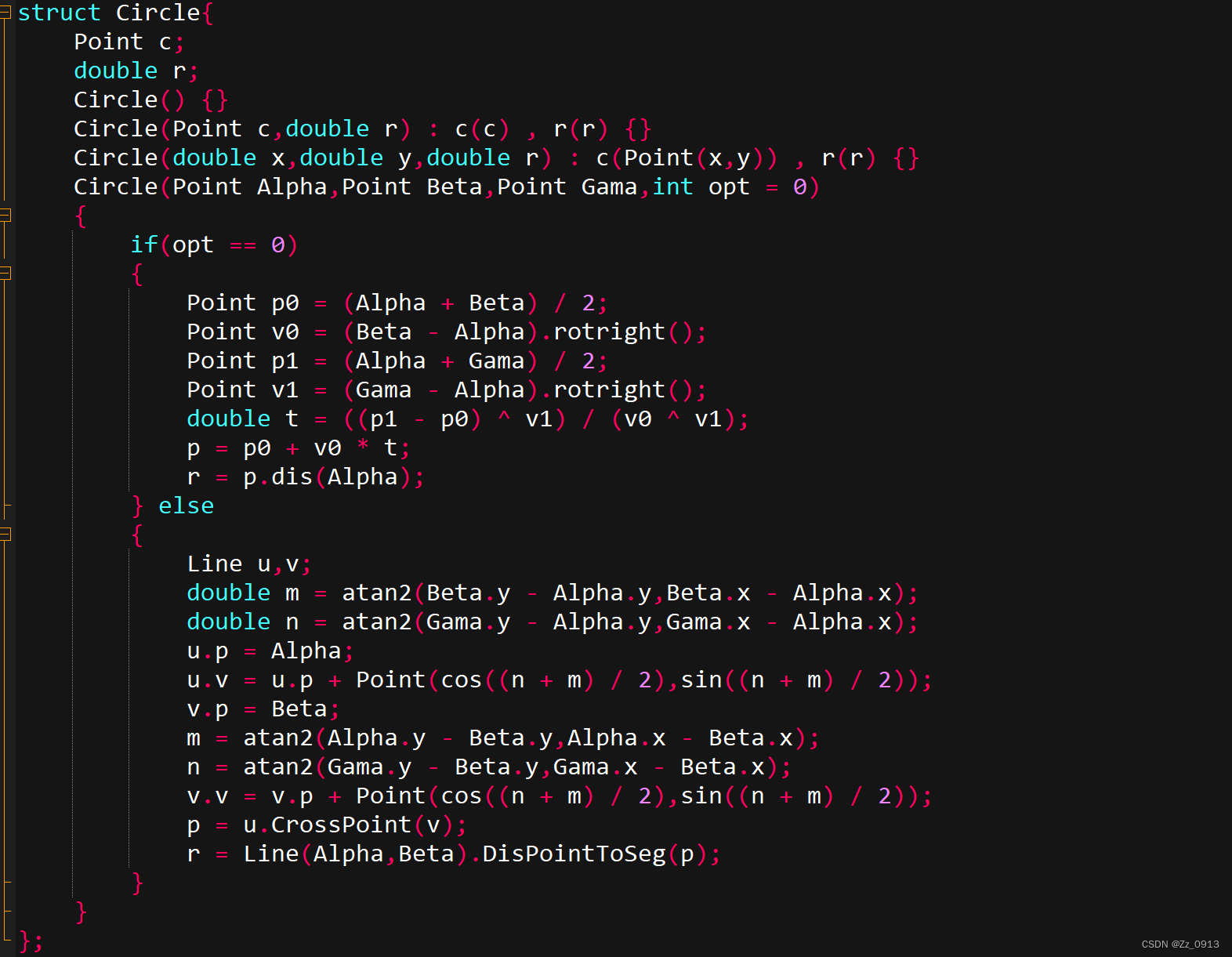
然后我们来看看有关圆的一些基本几何关系:
1.圆与直线的位置关系,包含相离,相切和相交,我们说计算几何是解析几何的一种,所以我们需要通过圆方程的计算来求得关系🤔。那么对于这类计算,可以参考下面的两幅图:
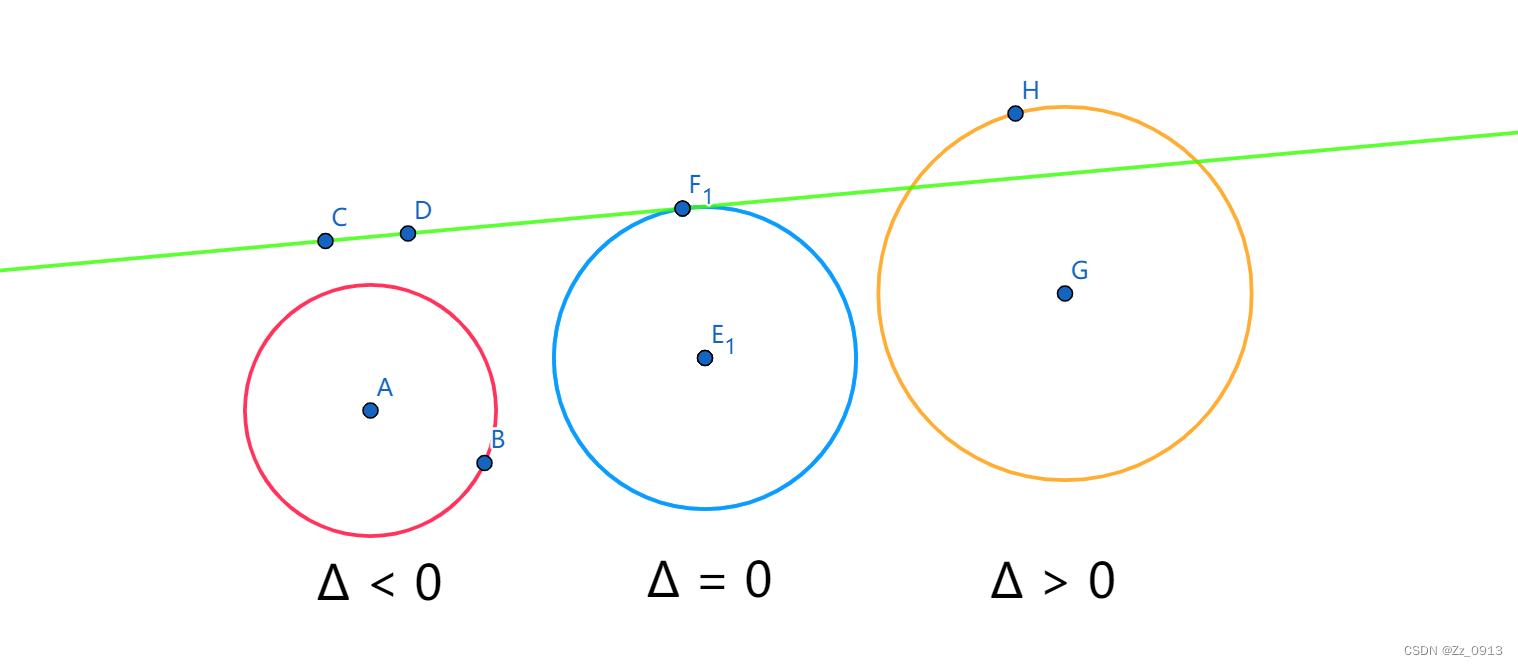
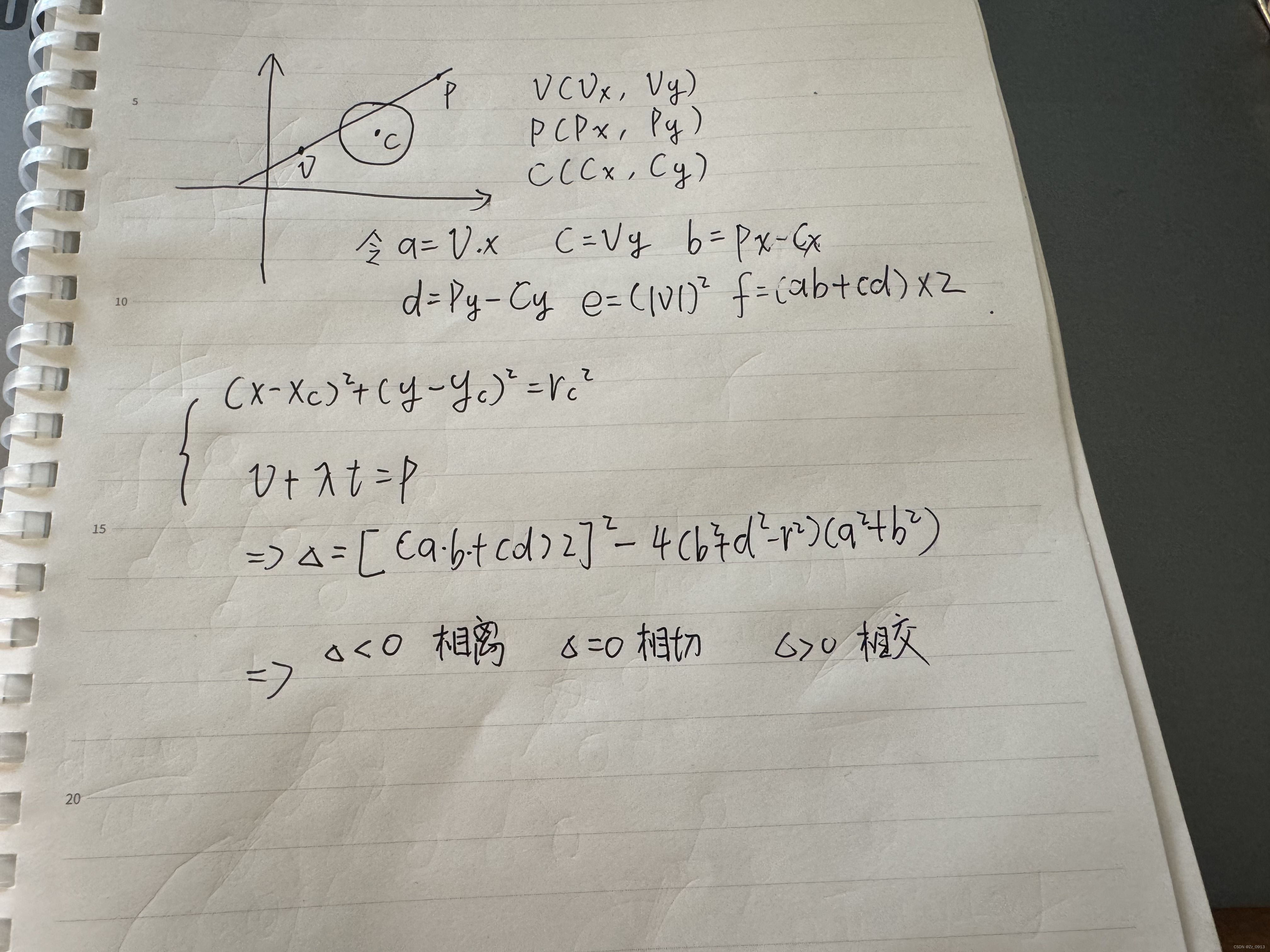
因此我们根据这个计算过程和原理可以轻而易举地写出这个判断函数辣~✌

2.两圆间的面积交
顾名思义,就是求两个圆之间的面积的交集,是一个非常简单非常基本的求解性质几何问 题。解题步骤也显而易见——我们首先判断两圆的位置关系:相离,外切,内切,内含,相交, 这些位置关系我们都只需要算出圆心距和两个半径就可以轻松得出,那么对于前四种位置关 系, 我们都可以一句话搞定了,主要是相交这一关系需要一定的推导:
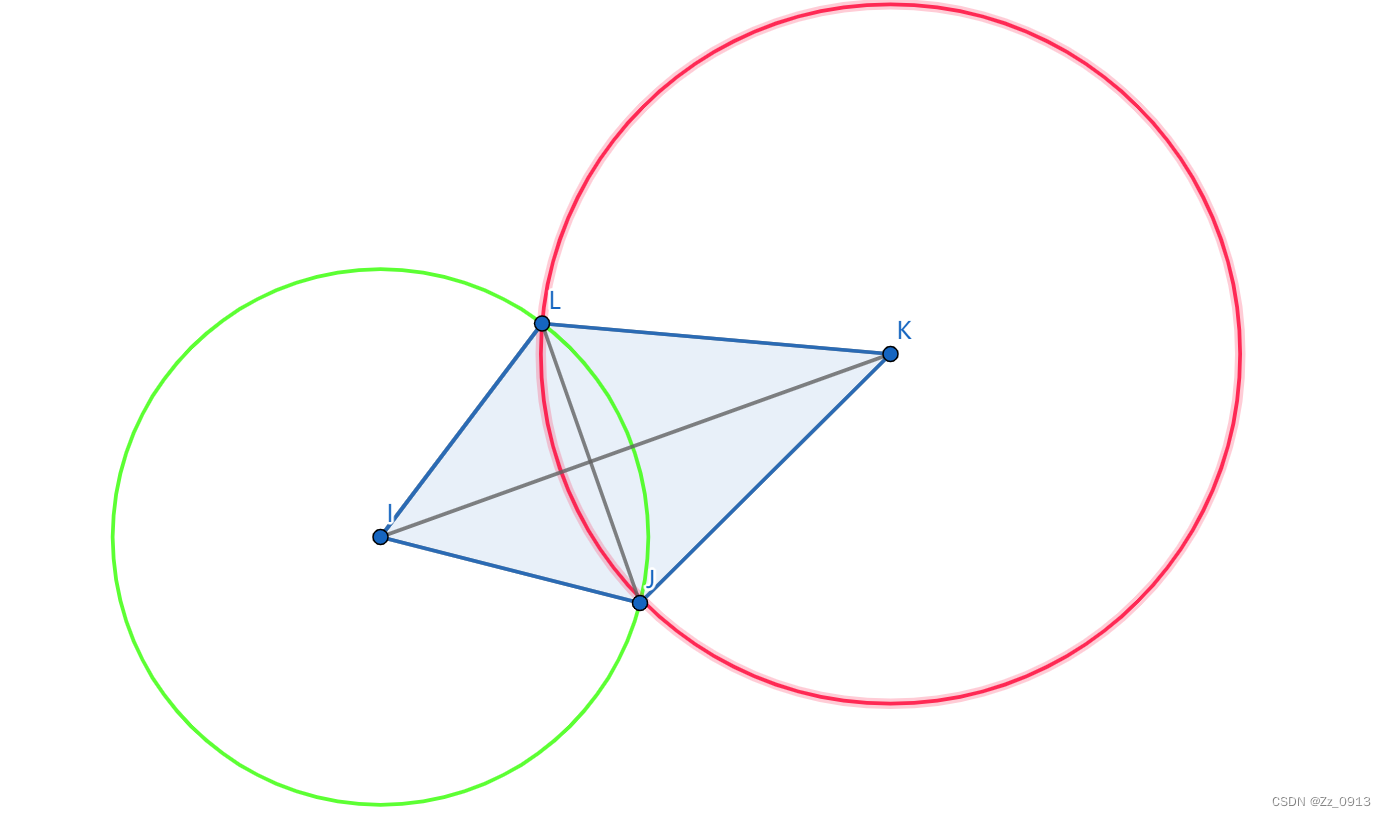
那么非常简单的,我们先通过向量叉积公式求出,蓝颜色部分的面积,即两个半径向量的 叉 积的绝对值,我们设为S0。然后通过部分圆面积公式求得弧LJ和弧JL在两个圆上的部分面积 和,设为S1,最终通过容斥原理可得,两圆相交面积为S1 - S0~😄,所以代码也是非常简单:
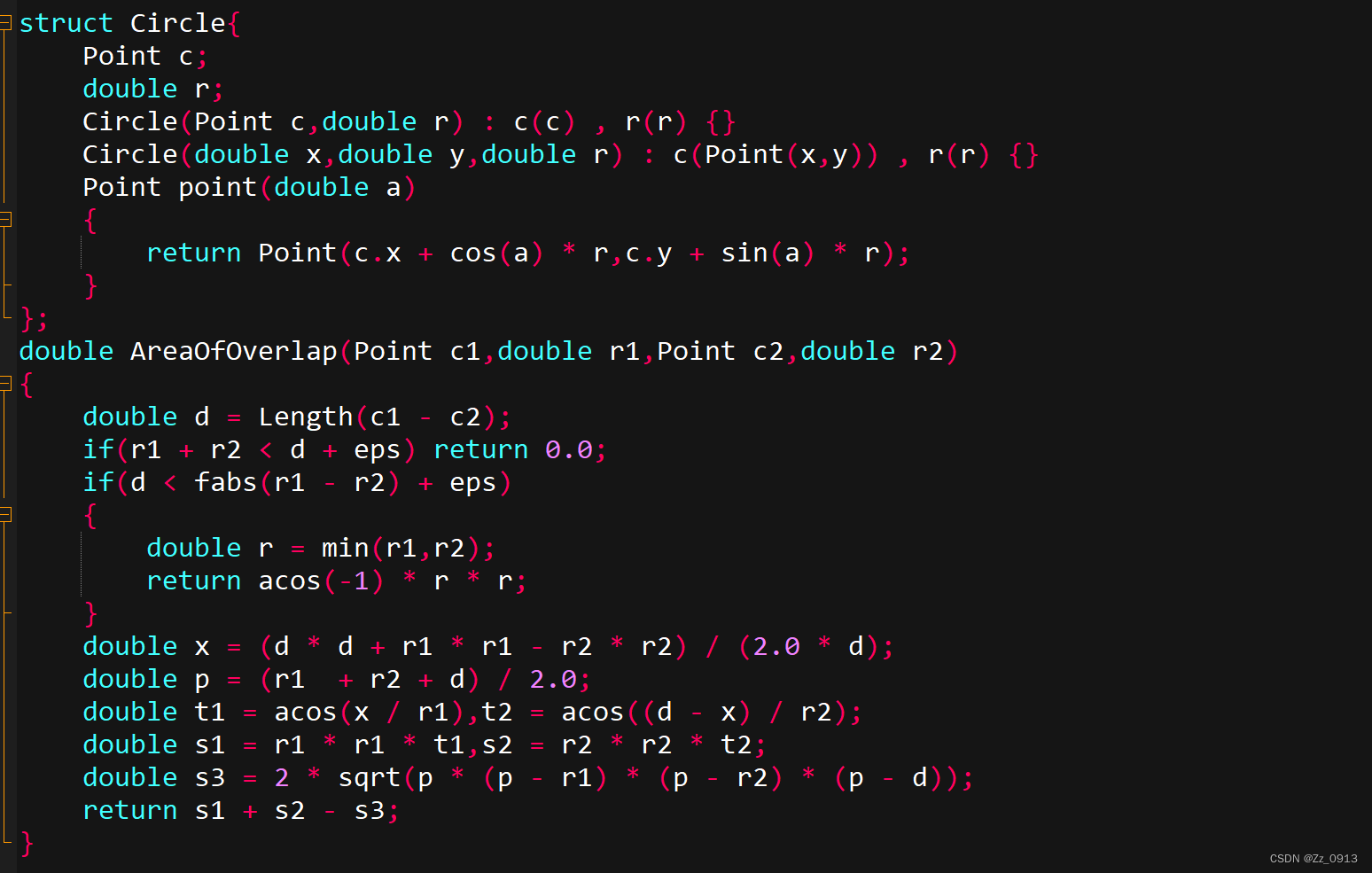
3.圆与多边形交的面积
任务:求圆与简单多边形的交的面积。圆心处于原点。
说明:按原点为中心将多边形三角剖分,这样只需要求一个三角形和圆的交的面积,则对于三角形OAB,有以下四种情况:
(1)AB都在圆内,此时计算三角形OAB的面积即可;
(2)A在圆内,B不在圆内,此时计算一个三角形的面积和一个扇形的面积;
(3)A不在圆内,B在圆内,此时计算一个三角形的面积和一个扇形的面积;
(4)AB都不在圆内,若AB与圆无交点,则计算一个扇形的面积,否则要计算两个扇形的面积和一个三角形的面积;
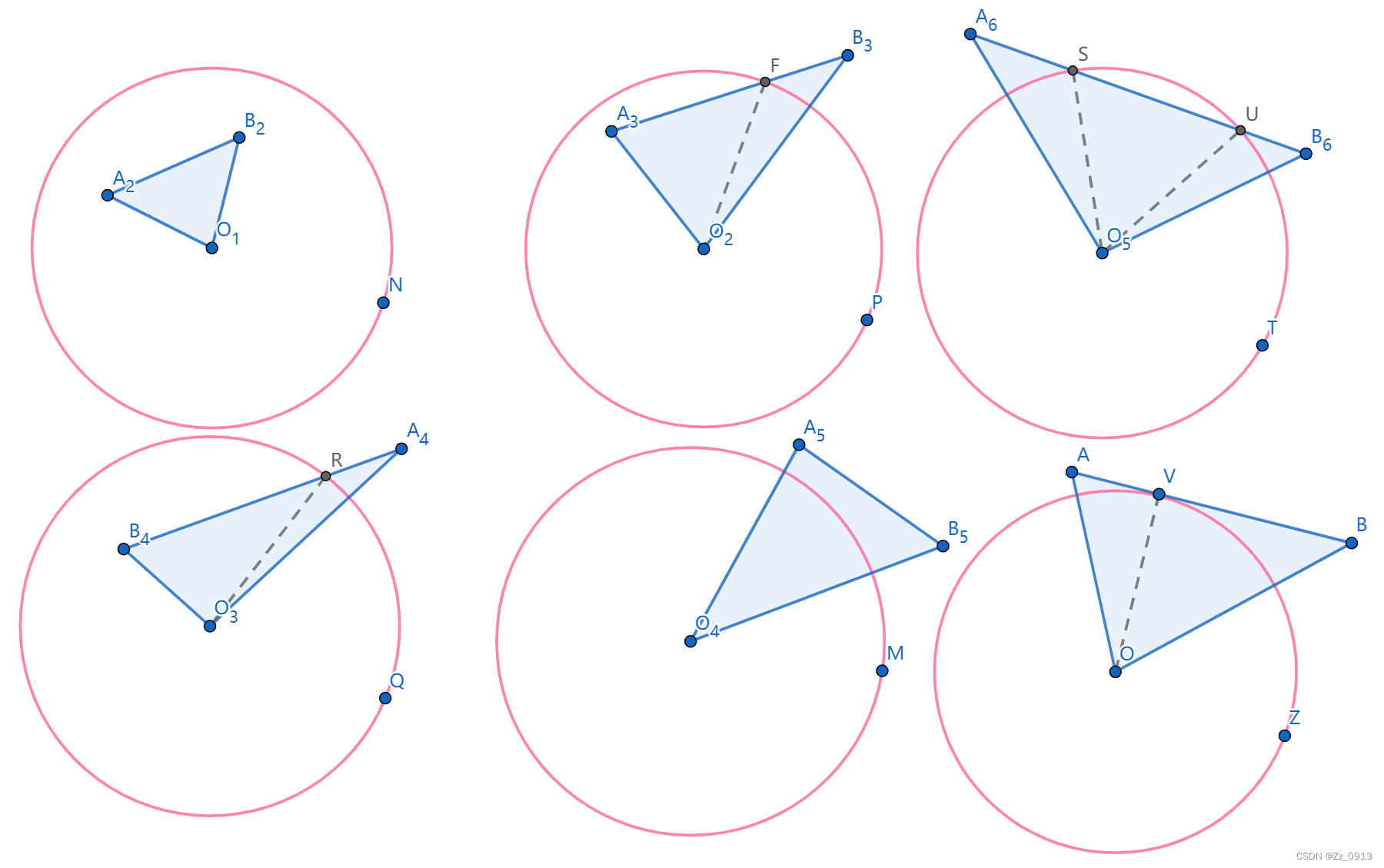
👆:是以原点(圆心)为一个顶点的三角形与圆的各种位置关系
因此思路已经非常透彻了,我们直接搬上代码:
#include<bits/stdc++.h>
using namespace std;
const double eps = 1e-9;
const int MAXN = 1e5 + 10;
const double pi = acos(-0.1L);
int Sign(double x)
{
if(fabs(x) < eps) return 0;
if(x > 0) return 1;
if(x < 0) return -1;
}
struct Point{
double x,y;
Point(double x = 0,double y = 0) : x(x) , y(y) {}
};
typedef Point Vector;
Vector operator + (Vector Alpha,Vector Beta)
{
return Vector(Alpha.x + Beta.x,Alpha.y + Beta.y);
}
Vector operator - (Vector Alpha,Vector Beta)
{
return Vector(Alpha.x - Beta.x,Alpha.y - Beta.y);
}
Vector operator * (Vector Alpha,double p)
{
return Vector(Alpha.x * p,Alpha.y * p);
}
Vector operator / (Vector Alpha,double p)
{
return Vector(Alpha.x / p,Alpha.y / p);
}
double Dot(Point Alpha,Point Beta)
{
return Alpha.x * Beta.x + Alpha.y * Beta.y;
}
double Cross(Point Alpha,Point Beta)
{
return Alpha.x * Beta.y - Alpha.y * Beta.x;
}
double abs(const Point &O)
{
return sqrt(Dot(O,O));
}
Point Crosspt(Point Alpha,Point Beta,Point P,Point Q)
{
double a1 = Cross(Beta - Alpha,P - Alpha);
double a2 = Cross(Beta - Alpha,Q - Alpha);
return (P * a2 - Q * a1) / (a2 - a1);
}
Point res[MAXN];
double r;
int n;
double mysqrt(double x)
{
return sqrt(max(0.0,x));
}
double Sector_Area(Point Alpha,Point Beta)
{
double Theta = atan2(Alpha.y,Alpha.x) - atan2(Beta.y,Beta.x);
while(Theta <= 0) Theta = Theta + 2 * pi;
while(Theta > 2 * pi) Theta = Theta - 2 * pi;
Theta = min(Theta,2 * pi - Theta);
return r * r * Theta / 2;
}
void circle_cross_line(Point Alpha,Point Beta,Point O,double r,Point ret[],int &num)
{
double x0 = O.x,y0 = O.y;
double x1 = Alpha.x,y1 = Alpha.y;
double x2 = Beta.x,y2 = Beta.y;
double dx = x2 - x1,dy = y2 - y1;
double A = dx * dx + dy * dy;
double B = 2 * dx * (x1 - x0) + 2 * dy * (y1 - y0);
double C = (x1 - x0) * (x1 - x0) + (y1 - y0) * (y1 - y0) - r * r;
double Delta = B * B - 4 * A * C;
num = 0;
if(Sign(Delta) >= 0){
double t1 = (-B - mysqrt(Delta)) / (2 * A);
double t2 = (-B + mysqrt(Delta)) / (2 * A);
if(Sign(t1 - 1) <= 0 && Sign(t1) >= 0)
{
ret[num] = Point(x1 + t1 * dx,y1 + t1 * dy);
num = num + 1;
}
if(Sign(t2 - 1) <= 0 && Sign(t2) >= 0)
{
ret[num] = Point(x1 + t2 * dx,y1 + t2 * dy);
num = num + 1;
}
}
}
double Calc(Point Alpha,Point Beta)
{
Point p[2];
int num = 0;
int ina = Sign(abs(Alpha) - r) < 0;
int inb = Sign(abs(Beta) - r) < 0;
if(ina)
{
if(inb)
{
return fabs(Cross(Alpha,Beta)) / 2.0;
}else
{
circle_cross_line(Alpha,Beta,Point(0,0),r,p,num);
return Sector_Area(Beta,p[0]) +fabs(Cross(Alpha,p[0])) / 2.0;
}
}else
{
if(inb)
{
circle_cross_line(Alpha,Beta,Point(0,0),r,p,num);
return Sector_Area(p[0],Alpha) + fabs(Cross(p[0],Beta)) / 2.0;
}else
{
circle_cross_line(Alpha,Beta,Point(0,0),r,p,num);
if(num == 2)
{
return Sector_Area(Alpha,p[0]) + Sector_Area(p[1],Beta)
+ fabs(Cross(p[0],p[1])) / 2.0;
}else
{
return Sector_Area(Alpha,Beta);
}
}
}
}
double Area()
{
double ret = 0;
for(int i = 0;i < n;i++)
{
int sgn = Sign(Cross(res[i],res[i + 1]));
if(sgn != 0) ret = ret + sgn * Calc(res[i],res[i + 1]);
}
return ret;
}
int main()
{
scanf("%d%lf",&n,&r);
for(int i = 0;i <= n - 1;i++)
{
double x,y;
scanf("%lf",&x);scanf("%lf",&y);
res[i].x = x,res[i].y = y;
}
res[n] = res[0];
printf("%.5f\n",Area());
return 0;
}
4.圆与圆的求交
意思就是让我们求出圆与圆之间的交点,那么我们解出这个问题首先直观地画一下示意图:
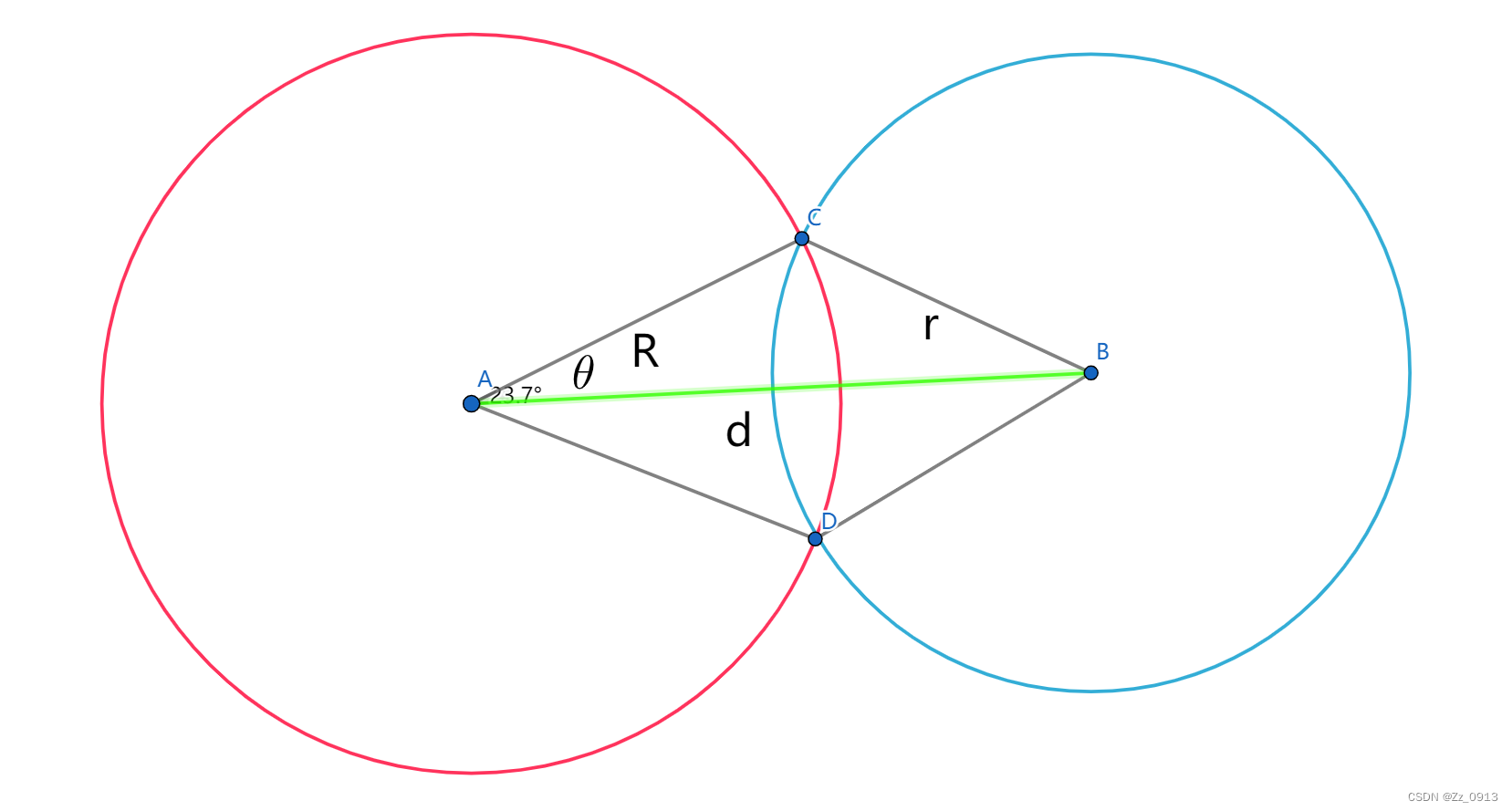
如图所示,设d=|AB|。由余弦定理,cosθ =(R^2 + d^2 - r^2)/(2Rd)。显然θ是锐角,所以可以计算出sinθ = sqrt(1 - (cosθ)^2)。利用平面向量旋转公式,将向量AB分别逆时针旋转θ度和逆时针旋转θ度,并将长度改变成R,就可以得到两个向量AD和AC。然后很容易就可以求出C和D。虽然利用了角度,但是代码中只有一次除法运算和一次开根运算,并没有涉及三角函数的运算,所以不会引入很大的精度误差。那么代码如下,省略大部分,给出最关键的一部分:

OK,到这里我们已经学完了圆类最基本的几个情况了,之后我会在《计算几何系列 ——— 闭合曲线之美(圆类-下)》中讲解随机增量法求最小圆覆盖,圆的面积并以及圆的离散化,可能在一定的思考后还会想到一些抽抽象象离离谱谱的小问题(但愿欧氏几何真的能融入计算几何叭),可以去刷一些计算几何的水题辣(POJ3675,SPOJ_CIRU)。






















 916
916











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








