Given a directed graph, find out whether the graph is strongly connected or not. A directed graph is strongly connected if there is a path between any two pair of vertices. For example, following is a strongly connected
graph.
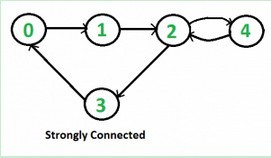
It is easy for undirected graph, we can just do a BFS and DFS starting from any vertex. If BFS or DFS visits all vertices, then
the given undirected graph is connected. This approach won’t work for a directed graph. For example, consider the
following graph which is not strongly connected. If we start DFS (or BFS) from vertex 0, we can reach all vertices, but if we
start from any other vertex, we cannot reach all vertices.
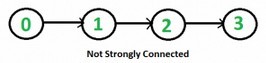
How to do for directed graph?
A simple idea is to use a all pair shortest path algorithm like Floyd Warshall or find Transitive Closure of graph. Time
complexity of this method would be O(v3).
We can also do DFS V times starting from every vertex. If any DFS, doesn’t visit all vertices, then graph is not strongly
connected. This algorithm takes O(V*(V+E)) time which can be same as transitive closure for a dense graph.
A better idea can be Strongly Connected Components (SCC) algorithm. We can find all SCCs in O(V+E) time. If number of
SCCs is one, then graph is strongly connected. The algorithm for SCC does extra work as it finds all SCCs.
Following is a simple DFS based algorithm that does two DFS traversals of graph:
1) Initialize all vertices as not visited.
2) Do a DFS traversal of graph starting from any arbitrary vertex v. If DFS traversal doesn’t visit all vertices, then return
false.
3) Reverse all arcs (or find transpose or reverse of graph)
4) Mark all vertices as not-visited in reversed graph.
5) Do a DFS traversal of reversed graph starting from same vertex v (Same as step 2). If DFS traversal doesn’t visit all
vertices, then return false. Otherwise return true.
The idea is, if every node can be reached from a vertex v, and every node can reach v, then the graph is strongly
connected. In step 2, we check if all vertices are reachable from v. In step 4, we check if all vertices can reach v (In reversed

It is easy for undirected graph, we can just do a BFS and DFS starting from any vertex. If BFS or DFS visits all vertices, then
the given undirected graph is connected. This approach won’t work for a directed graph. For example, consider the
following graph which is not strongly connected. If we start DFS (or BFS) from vertex 0, we can reach all vertices, but if we
start from any other vertex, we cannot reach all vertices.

How to do for directed graph?
A simple idea is to use a all pair shortest path algorithm like Floyd Warshall or find Transitive Closure of graph. Time
complexity of this method would be O(v3).
We can also do DFS V times starting from every vertex. If any DFS, doesn’t visit all vertices, then graph is not strongly
connected. This algorithm takes O(V*(V+E)) time which can be same as transitive closure for a dense graph.
A better idea can be Strongly Connected Components (SCC) algorithm. We can find all SCCs in O(V+E) time. If number of
SCCs is one, then graph is strongly connected. The algorithm for SCC does extra work as it finds all SCCs.
Following is a simple DFS based algorithm that does two DFS traversals of graph:
1) Initialize all vertices as not visited.
2) Do a DFS traversal of graph starting from any arbitrary vertex v. If DFS traversal doesn’t visit all vertices, then return
false.
3) Reverse all arcs (or find transpose or reverse of graph)
4) Mark all vertices as not-visited in reversed graph.
5) Do a DFS traversal of reversed graph starting from same vertex v (Same as step 2). If DFS traversal doesn’t visit all
vertices, then return false. Otherwise return true.
The idea is, if every node can be reached from a vertex v, and every node can reach v, then the graph is strongly
connected. In step 2, we check if all vertices are reachable from v. In step 4, we check if all vertices can reach v (In reversed
graph, if all vertices are reachable from v, then all vertices can reach v in original graph).
#include<iostream>
#include<list>
using namespace std;
class Graph {
int vexNum;
list<int>* adjacents;
public:
Graph(int _vexNum);
~Graph();
void addEdge(int v, int w);
void DFSUtil(int v, bool* visited);
bool isStrongConnected();
};
Graph::Graph(int _vexNum) {
vexNum = _vexNum;
adjacents = new list<int>[vexNum];
}
Graph::~Graph() {
delete []adjacents;
}
void Graph::addEdge(int v, int w) {
adjacents[v].push_back(w);
}
void Graph::DFSUtil(int v, bool* visited) {
visited[v] = true;
list<int>::iterator iter;
for (iter = adjacents[v].begin(); iter != adjacents[v].end(); iter++)
if (false == visited[*iter])
DFSUtil(*iter, visited);
}
bool Graph::isStrongConnected() {
bool* visited = new bool[vexNum];
int v;
for (v = 0; v < vexNum; v++)
visited[v] = false;
DFSUtil(0, visited);
for (v = 0; v < vexNum; v++)
if (false == visited[v]) {
delete []visited;
return false;
}
Graph gt = Graph(vexNum);
list<int>::iterator iter;
for (v = 0; v < vexNum; v++) {
for (iter = adjacents[v].begin(); iter != adjacents[v].end(); iter++)
gt.adjacents[*iter].push_back(v);
}
for (v = 0; v < vexNum; v++)
visited[v] = false;
gt.DFSUtil(0, visited);
for (v = 0; v < vexNum; v++)
if (false == visited[v]) {
delete []visited;
return false;
}
delete []visited;
return true;
}
int main(int argc, char* argv[]) {
Graph g1 = Graph(5);
g1.addEdge(0, 1);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.addEdge(3, 0);
g1.addEdge(2, 4);
g1.addEdge(4, 2);
if (g1.isStrongConnected())
cout << "yes" << endl;
else
cout << "non" << endl;
Graph g2(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
if (g2.isStrongConnected())
cout << "yes" << endl;
else
cout << "non" << endl;
cin.get();
return 0;
}







 本文介绍了一种用于判断有向图是否为强连通图的算法。通过两次深度优先搜索(DFS),首先从任意顶点出发遍历图,然后在反转后的图中再次从同一顶点出发遍历,如果所有顶点都能被访问到,则说明图是强连通的。
本文介绍了一种用于判断有向图是否为强连通图的算法。通过两次深度优先搜索(DFS),首先从任意顶点出发遍历图,然后在反转后的图中再次从同一顶点出发遍历,如果所有顶点都能被访问到,则说明图是强连通的。
















 660
660

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








