正交矩阵，（标准）正交基，正交投影，正交分解定理，最佳逼近定理，格拉姆-施密特方法求正交基（手算+MATLAB），QR分解（手算+MATLAB计算、分析）

正交（orthogonality）、正交集（orthogonal set）、单位正交集

定义：如果向量$u$和向量$v$是相互正交的，则有：$u\cdot v=0$。

因为对于零向量，都有$0^T\cdot v=0$，所以零向量与$R^n$中任意向量正交。

（零向量的默认形式写作$0=\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\end{array}\right]$）

$R^n$中的向量集合{$u_1$，$\dots$，$u_p$}中的任意两个不同的向量都正交，则此集合称为正交集。

如果正交集里面的向量都是单位向量（即长度都为1的向量），则此集合称为单位正交集，

如果单位正交集{$u_1$，$\dots$，$u_p$}生成子空间H，则{$u_1$，$\dots$，$u_p$}是H的单位正交基。

最简单的单位正交集是由$R^n$中的标准基组成的集合 { e 1 , e 2 , … , e n } \{e_1,e_2,\dots,e_n\} {e1​,e2​,…,en​}，集合 { e 1 , e 2 , … , e n } \{e_1,e_2,\dots,e_n\} {e1​,e2​,…,en​}的任一非空子集也是单位正交的。

例：

$u_1=\left[\begin{array}{c}3\\ 1\\ 1\end{array}\right]$，$u_2=\left[\begin{array}{c}-1\\ 2\\ 1\end{array}\right]$，$u_3=\left[\begin{array}{c}-\frac{1}{2}\\ -2\\ \frac{7}{2}\end{array}\right]$

因为$u_1\cdot u_2=0$，$u_2\cdot u_3=0$，$u_1\cdot u_3=0$，所以集合{$u_1$，$u_2$，$u_3$}是正交集。

如果 S = { u 1 , … , u p } S=\{u_1,\dots ,u_p\} S={u1​,…,up​}是由$R^n$中非零向量构成的正交集，则S是线性无关的集合，所以 S = { u 1 , … , u p } S=\{u_1,\dots ,u_p\} S={u1​,…,up​}是其所生成的子空间H的一组基。当然，反过来说也成立，即：$R^n$中子空间H的一个正交基不仅是H的一个基，同时也是一个正交集。

定理1：

{ u 1 , … , u p } \{u_1,\dots ,u_p\} {u1​,…,up​}是由$R^n$中子空间H的正交基，对H中每个向量$y$，线性组合$y=c_1{u}_1+\cdots +c_p{u}_p$中的权可以用公式$c_j=\frac{y\cdot u_j}{u_j\cdot u_j}$来计算。

例：

$u_1=\left[\begin{array}{c}3\\ 1\\ 1\end{array}\right]$，$u_2=\left[\begin{array}{c}-1\\ 2\\ 1\end{array}\right]$，$u_3=\left[\begin{array}{c}-\frac{1}{2}\\ -2\\ \frac{7}{2}\end{array}\right]$

由上述例子可知集合{$u_1$，$u_2$，$u_3$}是正交集，所以也是$R^3$中的一个正交基。请将$y=\left[\begin{array}{c}6\\ 1\\ -8\end{array}\right]$表示成为S中向量的线性组合。

解：
$y\cdot u_1=18+1-8=11$，$u_1\cdot u_1=9+1+1=11$
$y\cdot u_2=-6+2-8=-12$，$u_2\cdot u_2=1+4+1=6$
$y\cdot u_3=-3-2-28=-33$，$u_3\cdot u_3=\frac{1}{4}+4+\frac{49}{4}=\frac{33}{2}$

由上述定理得：

$y=\frac{y\cdot u_1}{u_1\cdot u_1}\cdot u_1+\frac{y\cdot u_2}{u_2\cdot u_2}\cdot u_2+\frac{y\cdot u_3}{u_3\cdot u_3}\cdot u_3=\frac{11}{11}{u}_1+\frac{-12}{6}{u}_2+\frac{-33}{\frac{33}{2}}{u}_3=u_1-2u_2-2u_3$

总结：由正交基构成的线性表示，如$y=u_1-2u_2-2u_3$，其中的权（$u_1$，$u_2$，$u_3$前面的数）是较容易由公式算出的。但是如果基不是正交的，则不能用上述公式计算权值，而要用解方程组，然后表示成参数向量形式的方式写出线性表示的式子。

定理2：

一个$m\times n$的矩阵$U$具有单位正交列向量的充要条件是$U^{T}U=I$。（这个矩阵$U$如果满足此条件，也叫正交矩阵）

例：矩阵$U=\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{2}{3}\\ \frac{1}{\sqrt{2}}& -\frac{2}{3}\\ 0& \frac{1}{3}\end{array}\right]$。

对于矩阵$U$的任两列：
${\left[\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\\ 0\end{array}\right]}^T\left[\begin{array}{c}\frac{2}{3}\\ -\frac{2}{3}\\ \frac{1}{3}\end{array}\right]=\frac{\sqrt{2}}{3}-\frac{\sqrt{2}}{3}+0=0$，正交。

且每列的模（即向量的长度，或叫范数）等于1，所以此矩阵具有单位正交列向量。

计算：

$U^{T}U=\left[\begin{array}{ccc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& 0\\ \frac{2}{3}& -\frac{2}{3}& \frac{1}{3}\end{array}\right]\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{2}{3}\\ \frac{1}{\sqrt{2}}& -\frac{2}{3}\\ 0& \frac{1}{3}\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=I$

所以，也可以推出此矩阵具有单位正交列向量。

定理3：

如果矩阵$U$是一个$m\times n$的且具有单位正交列的矩阵，且$x$和$y$是$R^n$中的向量，则：

1. $||Ux||=||x||$
2. $(Ux)\cdot (Uy)=x\cdot y$
3. $(Ux)\cdot (Uy)=0$的充要条件是$x\cdot y=0$.

例：对于上面的矩阵$U=\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{2}{3}\\ \frac{1}{\sqrt{2}}& -\frac{2}{3}\\ 0& \frac{1}{3}\end{array}\right]$，和$x=\left[\begin{array}{c}\sqrt{2}\\ 3\end{array}\right]$,。

由于矩阵$U$具有单位正交列向量，则：

$Ux=\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{2}{3}\\ \frac{1}{\sqrt{2}}& -\frac{2}{3}\\ 0& \frac{1}{3}\end{array}\right]\left[\begin{array}{c}\sqrt{2}\\ 3\end{array}\right]=\left[\begin{array}{c}3\\ -1\\ 1\end{array}\right]$

$||Ux||=\sqrt{9+1+1}=\sqrt{11}$
$||x||=\sqrt{2+9}=\sqrt{11}$

即$||Ux||=||x||$

总结：

1. 如果一个矩阵$U$可逆，且$U^{-1}=U^T$，则矩阵$U$为正交矩阵（orthogonal matrix）。这样的矩阵具有单位正交列。
2. 任何具有单位正交列的方阵都是正交矩阵。
3. 正交矩阵的每两行也都是单位正交的。

例：
矩阵$U=\left[\begin{array}{ccc}\frac{3}{\sqrt{11}}& -\frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{66}}\\ \frac{1}{\sqrt{11}}& \frac{2}{\sqrt{6}}& -\frac{4}{\sqrt{66}}\\ \frac{1}{\sqrt{11}}& \frac{1}{\sqrt{6}}& \frac{7}{\sqrt{66}}\end{array}\right]$

先考察其每两列：

${\left[\begin{array}{c}\frac{3}{\sqrt{11}}\\ \frac{1}{\sqrt{11}}\\ \frac{1}{\sqrt{11}}\end{array}\right]}^T\left[\begin{array}{c}-\frac{1}{\sqrt{6}}\\ \frac{2}{\sqrt{6}}\\ \frac{1}{\sqrt{6}}\end{array}\right]=-\frac{3}{\sqrt{66}}+\frac{2}{\sqrt{66}}+\frac{1}{\sqrt{66}}=0$

${\left[\begin{array}{c}\frac{3}{\sqrt{11}}\\ \frac{1}{\sqrt{11}}\\ \frac{1}{\sqrt{11}}\end{array}\right]}^T\left[\begin{array}{c}-\frac{1}{\sqrt{66}}\\ -\frac{4}{\sqrt{66}}\\ \frac{7}{\sqrt{66}}\end{array}\right]=-\frac{3}{\sqrt{11\times 66}}-\frac{4}{\sqrt{11\times 66}}+\frac{7}{\sqrt{11\times 66}}=0$

${\left[\begin{array}{c}-\frac{1}{\sqrt{6}}\\ \frac{2}{\sqrt{6}}\\ \frac{1}{\sqrt{6}}\end{array}\right]}^T\left[\begin{array}{c}-\frac{1}{\sqrt{66}}\\ -\frac{4}{\sqrt{66}}\\ \frac{7}{\sqrt{66}}\end{array}\right]=\frac{1}{\sqrt{6\times 66}}-\frac{8}{\sqrt{6\times 66}}+\frac{7}{\sqrt{6\times 66}}=0$

矩阵$U$的每两列都正交，且每列模为1，所以矩阵$U$具有单位正交列，所以矩阵$U$是正交矩阵。

再考察其每两行：
$\left[\begin{array}{ccc}\frac{3}{\sqrt{11}}& -\frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{66}}\end{array}\right]{\left[\begin{array}{ccc}\frac{1}{\sqrt{11}}& \frac{2}{\sqrt{6}}& -\frac{4}{\sqrt{66}}\end{array}\right]}^T=\frac{18}{66}-\frac{22}{66}+\frac{4}{66}=0$

$\left[\begin{array}{ccc}\frac{3}{\sqrt{11}}& -\frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{66}}\end{array}\right]{\left[\begin{array}{ccc}\frac{1}{\sqrt{11}}& \frac{1}{\sqrt{6}}& \frac{7}{\sqrt{66}}\end{array}\right]}^T=\frac{18}{66}-\frac{11}{66}-\frac{7}{66}=0$

$\left[\begin{array}{ccc}\frac{1}{\sqrt{11}}& \frac{2}{\sqrt{6}}& -\frac{4}{\sqrt{66}}\end{array}\right]{\left[\begin{array}{ccc}\frac{1}{\sqrt{11}}& \frac{1}{\sqrt{6}}& \frac{7}{\sqrt{66}}\end{array}\right]}^T=\frac{6}{66}+\frac{22}{66}-\frac{28}{66}=0$

且每行的向量的模也都是1，

所以，可以验证正交矩阵$U$同样也具有单位正交行。

正交补（Orthocomplement）

如果向量$z$与$R^n$的子空间W中的任意向量都正交，则称$z$正交于W。
与子空间W正交的向量$z$的全体组成的集合称为W的正交补。

例：直线L垂直于平面W，垂足为O，则L上的所有向量垂直于空间W，所以直线L（向量集合）为W的正交补。反之，W平面空间中所有向量垂直于直线L，所以W也是L空间的正交补。

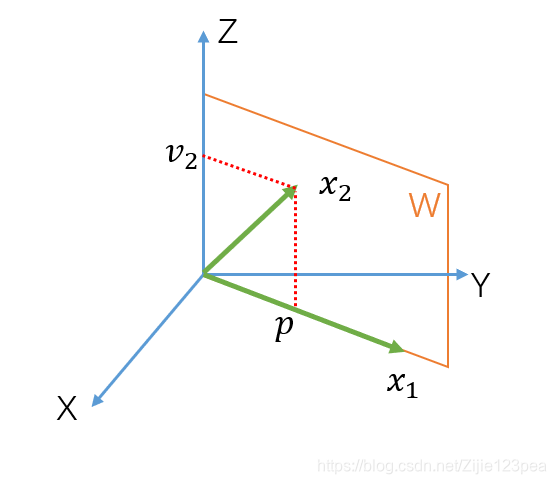
正交分解定理

若W是$R^n$的一个子空间，那么$R^n$中每一个向量$y$可以唯一表示为：$y=\hat{y}+z$
其中$\hat{y}$属于W，而$z$属于W的正交补（即正交于W的空间）。
如果 { u 1 , u 2 , … , u p } \{u_1,u_2,\dots,u_p\} {u1​,u2​,…,up​}是任意正交基，那么：
$\hat{y}=\frac{y\cdot u_1}{u_1\cdot u_1}{u}_1+\cdots +\frac{y\cdot u_p}{u_p\cdot u_p}{u}_p$

且$z=y-\hat{y}$，其中$\hat{y}$为$y$在W上的正交投影，记作$pro{j}_{w}y$。见下图。

例：
设$u_1=\left[\begin{array}{c}2\\ 5\\ -1\end{array}\right]$，$u_2=\left[\begin{array}{c}-2\\ 1\\ 1\end{array}\right]$，$y=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$，将$y$写成属于W的向量与正交于W的向量之和。

解：

$u_1\cdot u_2=0$，所以 { u 1 , u 2 } \{u_1,u_2\} {u1​,u2​}是 W = S p a n { u 1 , u 2 } W=Span\{u_1,u_2\} W=Span{u1​,u2​}的正交基。

由正交分解定理得：
先求$y$在W上的投影：
$\hat{y}=\frac{y\cdot u_1}{u_1\cdot u_1}{u}_1+\frac{y\cdot u_2}{u_2\cdot u_2}{u}_2=\frac{9}{30}\left[\begin{array}{c}2\\ 5\\ -1\end{array}\right]+\frac{3}{6}\left[\begin{array}{c}-2\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}\frac{-2}{5}\\ 2\\ \frac{1}{5}\end{array}\right]$

再求垂直于W的$z$（$z$属于W的正交补）：

$z=y-\hat{y}=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]-\left[\begin{array}{c}\frac{-2}{5}\\ 2\\ \frac{1}{5}\end{array}\right]=\left[\begin{array}{c}\frac{7}{5}\\ 0\\ \frac{14}{5}\end{array}\right]$

所以，可以得到$y$的分解式是：

$y=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]=\left[\begin{array}{c}\frac{7}{5}\\ 0\\ \frac{14}{5}\end{array}\right]+\left[\begin{array}{c}\frac{-2}{5}\\ 2\\ \frac{1}{5}\end{array}\right]$

可见，这样分解出来的两个向量一个是属于W的，另一个是正交与W的。

最佳逼近定理

  如果W是$R^n$的一个子空间，$y$是$R^n$中任意向量，$\hat{y}$是$y$在W上的正交投影，那么$\hat{y}$是W中最接近$y$的点，即有：$||y-\hat{y}||<||y-v||$对所有属于W，但又异于$\hat{y}$的$v$都成立。

  这里的$\hat{y}$也叫W中的元素对$y$的最佳逼近。

例如，在上例中，

$y$在W上的投影：
$\hat{y}=\frac{y\cdot u_1}{u_1\cdot u_1}{u}_1+\frac{y\cdot u_2}{u_2\cdot u_2}{u}_2=\frac{9}{30}\left[\begin{array}{c}2\\ 5\\ -1\end{array}\right]+\frac{3}{6}\left[\begin{array}{c}-2\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}\frac{-2}{5}\\ 2\\ \frac{1}{5}\end{array}\right]$

$\hat{y}$就是W中距离$y$最近的点。

由最佳逼近定理可得：从$y$到W的距离为$||y-\hat{y}||=\sqrt{\frac{49}{25}+\frac{196}{25}}=\sqrt{\frac{49}{5}}$

（$y-\hat{y}=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]-\left[\begin{array}{c}\frac{-2}{5}\\ 2\\ \frac{1}{5}\end{array}\right]=\left[\begin{array}{c}\frac{7}{5}\\ 0\\ \frac{14}{5}\end{array}\right]$）

格拉姆-施密特方法（Gram Schmidt method）

方法：对于$R^n$的子空间W的一个基 { x 1 , x 2 , … , x p } \{x_1,x_2,\dots,x_p\} {x1​,x2​,…,xp​}，定义：
$v_1=x_1$
$v_2=x_2-\frac{x_2\cdot v_1}{v_1\cdot v_1}{v}_1$
$v_3=x_3-\frac{x_3\cdot v_1}{v_1\cdot v_1}{v}_1-\frac{x_3\cdot v_2}{v_2\cdot v_2}{v}_2$
$\dots$
$v_p=x_p-\frac{x_p\cdot v_1}{v_1\cdot v_1}{v}_1-\frac{x_p\cdot v_2}{v_2\cdot v_2}{v}_2-\cdots -\frac{x_p\cdot v_{p-1}}{v_{p-1}\cdot v_{p-1}}{v}_{p-1}$
则 { v 1 , v 2 , … , v p } \{v_1,v_2,\dots,v_p\} {v1​,v2​,…,vp​}是W的一个正交基。
此外， S p a n { v 1 , … , v k } = S p a n { x 1 , … , x k } Span\{v_1,\dots ,v_k\}=Span\{x_1,\dots ,x_k\} Span{v1​,…,vk​}=Span{x1​,…,xk​}，其中$1\le k\le p$。

例1：
假设 W = S p a n { x 1 , x 2 } W=Span\{x_1,x_2\} W=Span{x1​,x2​}，其中$x_1=\left[\begin{array}{c}3\\ 6\\ 0\end{array}\right]$，$x_2=\left[\begin{array}{c}1\\ 2\\ 2\end{array}\right]$，构造 W = S p a n { x 1 , x 2 } W=Span\{x_1,x_2\} W=Span{x1​,x2​}的一个正交基。

解：

令$v_1=x_1$，$p$为$x_2$在$x_1$上的投影。令$v_2=x_2-p$为与$x_1$正交的$x_2$的分量，$v_2$属于W。

$v_2=x_2-p=x_2-\frac{x_2\cdot x_1}{x_1\cdot x_1}{x}_1=\left[\begin{array}{c}1\\ 2\\ 2\end{array}\right]-\frac{15}{45}\left[\begin{array}{c}3\\ 6\\ 0\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 2\end{array}\right]$

所以 { v 1 , v 2 } \{v_1,v_2\} {v1​,v2​}是空间W的非零向量构成的正交集，且因为dimW=2，所以 { v 1 , v 2 } \{v_1,v_2\} {v1​,v2​}是W的一个基，即W的正交基。

标准正交基（Orthonormal Basis）：

上例中，$v_1=\left[\begin{array}{c}3\\ 6\\ 0\end{array}\right]$，$v_2=\left[\begin{array}{c}0\\ 0\\ 2\end{array}\right]$， { v 1 , v 2 } \{v_1,v_2\} {v1​,v2​}是W的正交基，把它变成标准正交基，即把每个元素单位化即可：
$u_1=\frac{v_1}{||v_1||}=\frac{1}{\sqrt{45}}\left[\begin{array}{c}3\\ 6\\ 0\end{array}\right]=\left[\begin{array}{c}\frac{1}{\sqrt{5}}\\ \frac{2}{\sqrt{5}}\\ 0\end{array}\right]$
$u_2=\frac{v_2}{||v_2||}=\frac{1}{\sqrt{4}}\left[\begin{array}{c}0\\ 0\\ 2\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$

{ u 1 , u 2 } \{u_1,u_2\} {u1​,u2​}是W的标准正交基。

例2：
设$x_1=\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]$，$x_2=\left[\begin{array}{c}0\\ 1\\ 1\\ 1\end{array}\right]$，$x_3=\left[\begin{array}{c}0\\ 0\\ 1\\ 1\end{array}\right]$，请构造$R^4$子空间W的一个正交基。

解：

由于 { x 1 , x 2 , x 3 } \{x_1,x_2,x_3\} {x1​,x2​,x3​}是线性无关的，所以它们构成W的一个基。

先令$v_1=x_1$， W 1 = S p a n { x 1 } = S p a n { v 1 } W_1=Span\{x_1\}=Span\{v_1\} W1​=Span{x1​}=Span{v1​}

再取$v_2$等于$x_2$减去它在子空间$W_1$上投影所得的向量，即：
$v_2=x_2-p$为与$x_1$正交的$x_2$的分量，$v_2$属于W，且 { v 1 , v 2 } \{v_1,v_2\} {v1​,v2​}是由$x_1$，$x_2$所生成的子空间$W_2$的一个正交基。

$v_2=x_2-pro{j}_{W_1}{x}_2=x_2-\frac{x_2\cdot v_1}{v_1\cdot v_1}{v}_1=\left[\begin{array}{c}0\\ 1\\ 1\\ 1\end{array}\right]-\frac{3}{4}\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}-\frac{3}{4}\\ \frac{1}{4}\\ \frac{1}{4}\\ \frac{1}{4}\end{array}\right]$

当然，可以吧$v_2$的分数放缩成整数：

$v_1=\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]$，$v_2^{{}^{\prime }}=4v_2=\left[\begin{array}{c}-3\\ 1\\ 1\\ 1\end{array}\right]$

再取$v_3$是$x_3$减去它在子空间$W_2$上的投影所得的向量：

先用正交基 { v 1 , v 2 ′ } \{v_1,v_2^{'}\} {v1​,v2′​}计算$x_3$在$W_2$上的投影：

$pro{j}_{W_2}{x}_3=pro{j}_{v_1}{x}_3+pro{j}_{v_2^{{}^{\prime }}}{x}_3=\frac{x_3\cdot v_1}{v_1\cdot v_1}{v}_1+\frac{x_3\cdot v_2^{{}^{\prime }}}{v_2^{{}^{\prime }}\cdot v_2^{{}^{\prime }}}{v}_2^{{}^{\prime }}=\frac{2}{4}\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]+\frac{2}{12}\left[\begin{array}{c}-3\\ 1\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}0\\ \frac{2}{3}\\ \frac{2}{3}\\ \frac{2}{3}\end{array}\right]$

那么$v_3$是$x_3$正交于$W_2$的分量，即：

$v_3=x_3-pro{j}_{W_2}{x}_3=\left[\begin{array}{c}0\\ 0\\ 1\\ 1\end{array}\right]-\left[\begin{array}{c}0\\ \frac{2}{3}\\ \frac{2}{3}\\ \frac{2}{3}\end{array}\right]=\left[\begin{array}{c}0\\ -\frac{2}{3}\\ \frac{1}{3}\\ \frac{1}{3}\end{array}\right]$

所以 { v 1 , v 2 ′ , v 3 } \{v_1,v_2^{'},v_3\} {v1​,v2′​,v3​}是W的正交基。

QR分解

定理：如果$m\times n$的矩阵$A$各列线性无关，那么$A$可以分解为$A=QR$，其中$Q$为一个$m\times n$的矩阵，其各列形成Col A的一个标准正交基，$R$是一个$n\times n$的上三角可逆矩阵，且在对角线上的元素为正数。

例：
求矩阵$A=\left[\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$的一个QR分解。

矩阵$A$的列向量同上面例2的列向量：
$x_1=\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]$，$x_2=\left[\begin{array}{c}0\\ 1\\ 1\\ 1\end{array}\right]$，$x_3=\left[\begin{array}{c}0\\ 0\\ 1\\ 1\end{array}\right]$

C o l   A = S p a n { x 1 , x 2 , x 3 } Col\space A=Span\{x_1,x_2,x_3\} Col A=Span{x1​,x2​,x3​}的一个正交基在上面例2中求得为：
$v_1=\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]$，$v_2^{{}^{\prime }}=\left[\begin{array}{c}-3\\ 1\\ 1\\ 1\end{array}\right]$，$v_3=\left[\begin{array}{c}0\\ -\frac{2}{3}\\ \frac{1}{3}\\ \frac{1}{3}\end{array}\right]$

重新度量$v_3$，取$v_3^{{}^{\prime }}=3v_3=\left[\begin{array}{c}0\\ -2\\ 1\\ 1\end{array}\right]$

将$v_1$，$v_2^{{}^{\prime }}$和$v_3^{{}^{\prime }}$单位化：
$u_1=\frac{v_1}{||v_1||}=\frac{1}{\sqrt{4}}\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}\frac{1}{2}\\ \frac{1}{2}\\ \frac{1}{2}\\ \frac{1}{2}\end{array}\right]$

$u_2=\frac{v_2^{{}^{\prime }}}{||v_2^{{}^{\prime }}||}=\frac{1}{\sqrt{12}}\left[\begin{array}{c}-3\\ 1\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}-\frac{3}{\sqrt{12}}\\ \frac{1}{\sqrt{12}}\\ \frac{1}{\sqrt{12}}\\ \frac{1}{\sqrt{12}}\end{array}\right]$

$u_3=\frac{v_3^{{}^{\prime }}}{||v_3^{{}^{\prime }}||}=\frac{1}{\sqrt{6}}\left[\begin{array}{c}0\\ -2\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}0\\ -\frac{2}{\sqrt{6}}\\ \frac{1}{\sqrt{6}}\\ \frac{1}{\sqrt{6}}\end{array}\right]$

根据QR分解定理：$Q$矩阵是待分解矩阵$A$的列空间的标准正交基，所以：

$Q=[u_1{u}_2{u}_3]=\left[\begin{array}{ccc}\frac{1}{2}& -\frac{3}{\sqrt{12}}& 0\\ \frac{1}{2}& \frac{1}{\sqrt{12}}& -\frac{2}{\sqrt{6}}\\ \frac{1}{2}& \frac{1}{\sqrt{12}}& \frac{1}{\sqrt{6}}\\ \frac{1}{2}& \frac{1}{\sqrt{12}}& \frac{1}{\sqrt{6}}\end{array}\right]$

由正交定理2可知，矩阵$Q$的每两列都是正交的且是标准正交的，所以，有$Q^{T}Q=I$。

QR分解是将$A$可以分解为$A=QR$，所以：$Q^{T}A=Q^T(QR)=IR=R$

这表明，可以根据$R=Q^{T}A$来求得$R$矩阵。

所以，本例中：
$R=Q^{T}A=\left[\begin{array}{cccc}\frac{1}{2}& \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\\ -\frac{3}{\sqrt{12}}& \frac{1}{\sqrt{12}}& \frac{1}{\sqrt{12}}& \frac{1}{\sqrt{12}}\\ 0& -\frac{2}{\sqrt{6}}& \frac{1}{\sqrt{6}}& \frac{1}{\sqrt{6}}\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]=\left[\begin{array}{ccc}2& \frac{3}{2}& 1\\ 0& \frac{3}{\sqrt{12}}& \frac{2}{\sqrt{12}}\\ 0& 0& \frac{2}{\sqrt{6}}\end{array}\right]$

验算：

$QR=\left[\begin{array}{ccc}\frac{1}{2}& -\frac{3}{\sqrt{12}}& 0\\ \frac{1}{2}& \frac{1}{\sqrt{12}}& -\frac{2}{\sqrt{6}}\\ \frac{1}{2}& \frac{1}{\sqrt{12}}& \frac{1}{\sqrt{6}}\\ \frac{1}{2}& \frac{1}{\sqrt{12}}& \frac{1}{\sqrt{6}}\end{array}\right]\left[\begin{array}{ccc}2& \frac{3}{2}& 1\\ 0& \frac{3}{\sqrt{12}}& \frac{2}{\sqrt{12}}\\ 0& 0& \frac{2}{\sqrt{6}}\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]=A$

所以此QR分解正确。

MATLAB中QR分解的方法

  在MATLAB中，可以使用命令[Q R]=qr(A)来对矩阵$A$进行QR分解。该命令会生成一个标准正交的方针Q和一个上三角矩阵R。
例如，对上述例子，求矩阵$A=\left[\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$的一个QR分解。

A =
     1     0     0
     1     1     0
     1     1     1
     1     1     1
     
>> [Q R]=qr(A)
Q =
   -0.5000    0.8660         0    0.0000
   -0.5000   -0.2887    0.8165   -0.0000
   -0.5000   -0.2887   -0.4082   -0.7071
   -0.5000   -0.2887   -0.4082    0.7071
R =
   -2.0000   -1.5000   -1.0000
         0   -0.8660   -0.5774
         0         0   -0.8165
         0         0         0

  可见，MATLAB分解出来的$R$矩阵和计算出来的$R$矩阵中的每个元素是与原来$R=\left[\begin{array}{ccc}2& \frac{3}{2}& 1\\ 0& \frac{3}{\sqrt{12}}& \frac{2}{\sqrt{12}}\\ 0& 0& \frac{2}{\sqrt{6}}\end{array}\right]$每个元素互为相反数的，此外，还在最下面多了一行的0；

且MATLAB分解出来的$Q$矩阵与手算分解出来的$Q=\left[\begin{array}{ccc}\frac{1}{2}& -\frac{3}{\sqrt{12}}& 0\\ \frac{1}{2}& \frac{1}{\sqrt{12}}& -\frac{2}{\sqrt{6}}\\ \frac{1}{2}& \frac{1}{\sqrt{12}}& \frac{1}{\sqrt{6}}\\ \frac{1}{2}& \frac{1}{\sqrt{12}}& \frac{1}{\sqrt{6}}\end{array}\right]$是有差别的，除了每个元素互为相反数外，最右边多了一列：

$\left[\begin{array}{c}0\\ -0\\ -0.7071\\ 0.7071\end{array}\right]$；显然，这个分解出来的Q矩阵尽管多了最右边这一列，却也是标准正交的（orthonormal）。

  可见，MATLAB分解出来的矩阵，虽然和手算的矩阵有差别，但是显然也是符合$A=QR$这个基本要求的，MATLAB分解出来的Q和R矩阵尺寸都是与A相同的。

  由上面的定理2：一个$m\times n$的矩阵$U$具有单位正交列向量的充要条件是$U^{T}U=I$。（这个矩阵$U$如果满足此条件，也叫正交矩阵）。以此检验MATLAB分解出来的矩阵$Q$是不是正交矩阵：

>> Q
Q =
   -0.5000    0.8660         0    0.0000
   -0.5000   -0.2887    0.8165   -0.0000
   -0.5000   -0.2887   -0.4082   -0.7071
   -0.5000   -0.2887   -0.4082    0.7071
   
>> Q'    //Q的转置
ans =
   -0.5000   -0.5000   -0.5000   -0.5000
    0.8660   -0.2887   -0.2887   -0.2887
         0    0.8165   -0.4082   -0.4082
    0.0000   -0.0000   -0.7071    0.7071

>> Q'*Q
ans =
    1.0000         0         0         0
         0    1.0000         0         0
         0         0    1.0000   -0.0000
         0         0   -0.0000    1.0000

  可见，MATLAB计算出来的矩阵$Q$满足关系$Q^{T}Q=I$，所以矩阵$Q$是正交矩阵。

  存在差别的原因：手算的QR分解是基于格拉姆-施密特方法的，其计算思路是，先以一个向量为一个基底，然后求与此向量垂直的向量并以之作另一个基底，然后再求与前面这两个相互垂直的基底都垂直的基底，然后再依次求下去，最终得到一组正交基。但是这个方法在计算具有很多列的矩阵的时候，由于浮点计算的误差，得到的正交基中的向量越来越不正交（误差越来越大）。

  所以MATLAB中的QR分解方法是经过优化的数值计算方法，可以处理很大的矩阵。

例：计算矩阵$A=\left[\begin{array}{ccc}1& 2& 5\\ -1& 1& -4\\ -1& 4& -3\\ 1& -4& 7\\ 1& 2& 1\end{array}\right]$的QR分解（手算加MATLAB）。

解：
列向量分别是：
$x_1=\left[\begin{array}{c}1\\ -1\\ -1\\ 1\\ 1\end{array}\right]$，$x_2=\left[\begin{array}{c}2\\ 1\\ 4\\ -4\\ 2\end{array}\right]$，$x_3=\left[\begin{array}{c}5\\ -4\\ -3\\ 7\\ 1\end{array}\right]$，
令$v_1=x_1=\left[\begin{array}{c}1\\ -1\\ -1\\ 1\\ 1\end{array}\right]$

求垂直于$v_1$的$v_2$：
$v_2=x_2-\frac{x_2\cdot v_1}{v_1\cdot v_1}{v}_1=\left[\begin{array}{c}2\\ 1\\ 4\\ -4\\ 2\end{array}\right]-\frac{-5}{5}\left[\begin{array}{c}1\\ -1\\ -1\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}3\\ 0\\ 3\\ -3\\ 3\end{array}\right]$，
重新度量$v_2^{{}^{\prime }}=\frac{1}{3}{v}_2=\left[\begin{array}{c}1\\ 0\\ 1\\ -1\\ 1\end{array}\right]$

求垂直于 W 2 = S p a n { v 1 , v 2 ′ } W_2=Span\{v_1,v_2^{'}\} W2​=Span{v1​,v2′​}的$v_3$：
$pro{j}_{W_2}{x}_3=pro{j}_{v_1}{x}_3+pro{j}_{v_2^{{}^{\prime }}}{x}_3=\frac{x_3\cdot v_1}{v_1\cdot v_1}{v}_1+\frac{x_3\cdot v_2^{{}^{\prime }}}{v_2^{{}^{\prime }}\cdot v_2^{{}^{\prime }}}{v}_2^{{}^{\prime }}=\frac{20}{5}\left[\begin{array}{c}1\\ -1\\ -1\\ 1\\ 1\end{array}\right]+\frac{-4}{4}\left[\begin{array}{c}1\\ 0\\ 1\\ -1\\ 1\end{array}\right]=\left[\begin{array}{c}3\\ -4\\ -5\\ 5\\ 3\end{array}\right]$
$v_3=x_3-pro{j}_{W_2}{x}_3=\left[\begin{array}{c}5\\ -4\\ -3\\ 7\\ 1\end{array}\right]-\left[\begin{array}{c}3\\ -4\\ -5\\ 5\\ 3\end{array}\right]=\left[\begin{array}{c}2\\ 0\\ 2\\ 2\\ -2\end{array}\right]$
重新度量$v_3^{{}^{\prime }}=\frac{1}{2}{v}_3=\left[\begin{array}{c}1\\ 0\\ 1\\ 1\\ -1\end{array}\right]$

所以 { v 1 , v 2 ′ , v 3 ′ } \{v_1,v_2^{'},v_3^{'}\} {v1​,v2′​,v3′​}是$R^5$子空间W的一组正交基。
将它们单位化后，可以组成$Q$矩阵：
$u_1=\frac{v_1}{||v_1||}=\frac{1}{\sqrt{5}}\left[\begin{array}{c}1\\ -1\\ -1\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}\frac{1}{\sqrt{5}}\\ -\frac{1}{\sqrt{5}}\\ -\frac{1}{\sqrt{5}}\\ \frac{1}{\sqrt{5}}\\ \frac{1}{\sqrt{5}}\end{array}\right]$

$u_2=\frac{v_2^{{}^{\prime }}}{||v_2^{{}^{\prime }}||}=\frac{1}{\sqrt{4}}\left[\begin{array}{c}1\\ 0\\ 1\\ -1\\ 1\end{array}\right]=\left[\begin{array}{c}\frac{1}{2}\\ 0\\ \frac{1}{2}\\ -\frac{1}{2}\\ \frac{1}{2}\end{array}\right]$

$u_3=\frac{v_3^{{}^{\prime }}}{||v_3^{{}^{\prime }}||}=\frac{1}{\sqrt{4}}\left[\begin{array}{c}1\\ 0\\ 1\\ 1\\ -1\end{array}\right]=\left[\begin{array}{c}\frac{1}{2}\\ 0\\ \frac{1}{2}\\ \frac{1}{2}\\ -\frac{1}{2}\end{array}\right]$

所以$Q=[u_1{u}_2{u}_3]=\left[\begin{array}{ccc}\frac{1}{\sqrt{5}}& \frac{1}{2}& \frac{1}{2}\\ -\frac{1}{\sqrt{5}}& 0& 0\\ -\frac{1}{\sqrt{5}}& \frac{1}{2}& \frac{1}{2}\\ \frac{1}{\sqrt{5}}& -\frac{1}{2}& \frac{1}{2}\\ \frac{1}{\sqrt{5}}& \frac{1}{2}& -\frac{1}{2}\end{array}\right]$

求$R$矩阵：
$R=Q^{T}A=\left[\begin{array}{ccccc}\frac{1}{\sqrt{5}}& -\frac{1}{\sqrt{5}}& -\frac{1}{\sqrt{5}}& \frac{1}{\sqrt{5}}& \frac{1}{\sqrt{5}}\\ \frac{1}{2}& 0& \frac{1}{2}& -\frac{1}{2}& \frac{1}{2}\\ \frac{1}{2}& 0& \frac{1}{2}& \frac{1}{2}& -\frac{1}{2}\end{array}\right]\left[\begin{array}{ccc}1& 2& 5\\ -1& 1& -4\\ -1& 4& -3\\ 1& -4& 7\\ 1& 2& 1\end{array}\right]=\left[\begin{array}{ccc}\sqrt{5}& -\sqrt{5}& 4\sqrt{5}\\ 0& 6& -2\\ 0& 0& 4\end{array}\right]$

验算：

$QR=\left[\begin{array}{ccc}\frac{1}{\sqrt{5}}& \frac{1}{2}& \frac{1}{2}\\ -\frac{1}{\sqrt{5}}& 0& 0\\ -\frac{1}{\sqrt{5}}& \frac{1}{2}& \frac{1}{2}\\ \frac{1}{\sqrt{5}}& -\frac{1}{2}& \frac{1}{2}\\ \frac{1}{\sqrt{5}}& \frac{1}{2}& -\frac{1}{2}\end{array}\right]\left[\begin{array}{ccc}\sqrt{5}& -\sqrt{5}& 4\sqrt{5}\\ 0& 6& -2\\ 0& 0& 4\end{array}\right]=\left[\begin{array}{ccc}1& 2& 5\\ -1& 1& -4\\ -1& 4& -3\\ 1& -4& 7\\ 1& 2& 1\end{array}\right]=A$

所以此QR分解成立。

在MATLAB中计算QR分解：

A =
     1     2     5
    -1     1    -4
    -1     4    -3
     1    -4     7
     1     2     1
>> [Q R]=qr(A)
Q =
   -0.4472   -0.5000   -0.5000   -0.0236   -0.5472
    0.4472   -0.0000    0.0000    0.8000   -0.4000
    0.4472   -0.5000   -0.5000    0.0236    0.5472
   -0.4472    0.5000   -0.5000    0.4236    0.3472
   -0.4472   -0.5000    0.5000    0.4236    0.3472
R =
   -2.2361    2.2361   -8.9443
         0   -6.0000    2.0000
         0         0   -4.0000
         0         0         0
         0         0         0

  可见，由MATLAB的qr( )函数计算出来的QR分解，对于矩阵$Q$，手算为$5\times 3$矩阵，MATLAB算出来为$5\times 5$矩阵，两者的符号是相反的。两个矩阵$R$的符号也是相反的，MATLAB的$R$矩阵下面多了一排0。

  相当于MATLAB是先把手算出来的$Q$矩阵在右边多补两列，并使之成为一个标准正交的方阵$Q_1$（这里是5X3变成5X5），然后在$R$下面增加0的行，使之与$Q_1$矩阵能相乘匹配（这里是3X3变成3X5）,这样最后乘出来的矩阵尺寸与A相同，并且满足QR分解的约束。

MATLAB中使用格拉姆-施密特方法求标准正交矩阵

  由上面的实验可知，MATLAB中的qr( )函数计算QR分解并非采用格拉姆-施密特方法求解，但是MATLAB中也提供了格拉姆-施密特方法求解正交基的函数，还是上面的矩阵，如下：

A =
     1     2     5
    -1     1    -4
    -1     4    -3
     1    -4     7
     1     2     1
>> G = gs(A)
 Matrix U with orthogonal columns:
U =
     1     3     2
    -1     0     0
    -1     3     2
     1    -3     2
     1     3    -2
rational display:
U =
       1              3              2       
      -1              0              0       
      -1              3              2       
       1             -3              2       
       1              3             -2       
Do you want columns normalized (1/0)? 1
matrix after normalizing columns: 
G =
    0.4472    0.5000    0.5000
   -0.4472         0         0
   -0.4472    0.5000    0.5000
    0.4472   -0.5000    0.5000
    0.4472    0.5000   -0.5000

  可见，使用函数gs( )求出来的正交矩阵，在标准后（运行函数会提示是否标准化，输入1确认）得到标准正交矩阵$G$，而这个矩阵$G$和手算出来的$Q$矩阵是一致的。