图像处理理论（二）——形态学、边缘检测、图像金字塔

http://antkillerfarm.github.io/

膨胀与腐蚀(Dilation & Erosion)

腐蚀和膨胀是对白色部分（高亮部分）而言的，不是黑色部分。膨胀就是图像中的高亮部分进行膨胀，“领域扩张”，效果图拥有比原图更大的高亮区域。腐蚀就是原图中的高亮部分被腐蚀，“领域被蚕食”，效果图拥有比原图更小的高亮区域。

具体方法如下：

1.膨胀。

$$g(i,j)=max_{k,l}f(i,j)$$

2.腐蚀。

$$g(i,j)=min_{k,l}f(i,j)$$

这里仿照C语言的记法，将膨胀操作记为$dilate(src)$，其中src表示源图像。同理，将腐蚀操作记为$erode(src)$。

效果如下：

膨胀和腐蚀不仅是基本的形态学操作，而且也是一种滤波器。它们和中值滤波一样，都是百分比（percentile）滤波的特例。当百分比为100%时，为最大值滤波，即膨胀操作；当百分比为0%时，为最小值滤波，即腐蚀操作；当百分比为50%时，即为中值滤波。

高级形态学操作

1.开运算（Opening Operation）

$$open(src)=dilate(erode(src))$$

开运算可以用来消除小物体、在纤细点处分离物体、平滑较大物体的边界的同时并不明显改变其面积。

2.闭运算(Closing Operation)

$$close(src)=erode(dilate(src))$$

闭运算能够排除小型黑洞(黑色区域)。

3.形态学梯度（Morphological Gradient）

$$morphgrad(src)=dilate(src)-erode(src)$$

对二值图像进行这一操作可以将团块（blob）的边缘突出出来。我们可以用形态学梯度来保留物体的边缘轮廓。

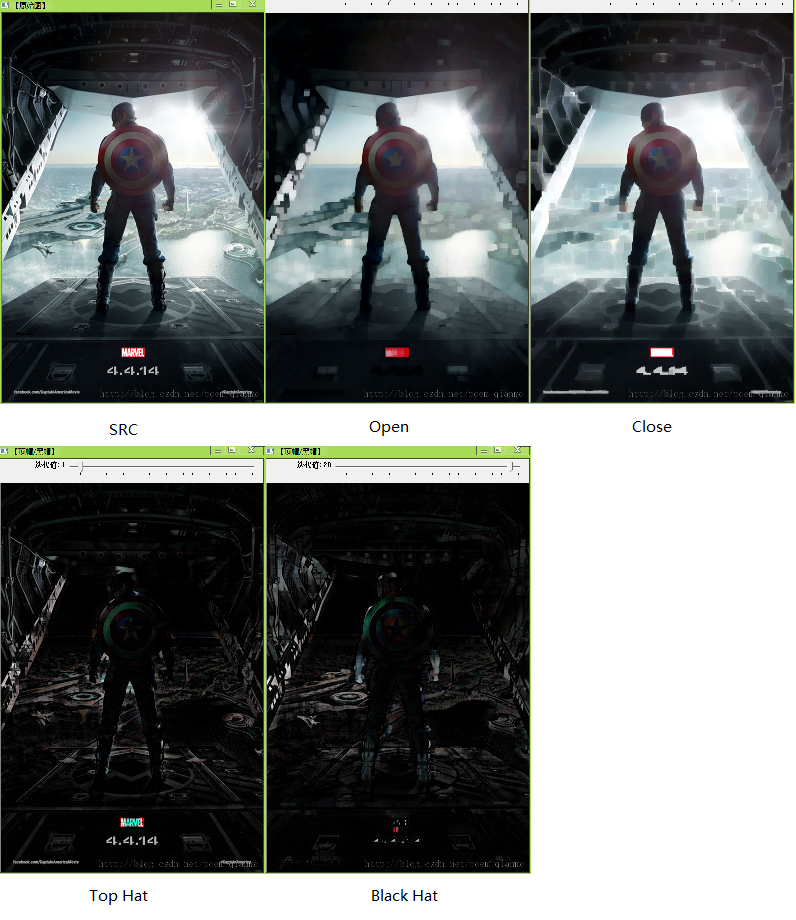
4.顶帽（Top Hat）

$$tophat(src)=src-open(src)$$

顶帽运算往往用来分离比邻近点亮一些的斑块。当一幅图像具有大幅的背景的时候，而微小物品比较有规律的情况下，可以使用顶帽运算进行背景提取。

5.黑帽（Black Hat）

$$blackhat(src)=close(src)-src$$

黑帽运算后的效果图突出了比原图轮廓周围的区域更暗的区域。

效果如下：

边缘检测

梯度

从数学概念上来说，一维梯度G，实际上就是函数的斜率，也就是一阶导数。二维梯度G是个向量，一般用两个维度上的偏导数$G_x$和$G_y$来刻画，即$G=[G_x,G_y]$。显然，沿梯度向量方向，函数值增加最快。

梯度向量求模的常见方法有：

$$G=|G_x|+|G_y|(模1)$$

$$G=\sqrt{G_x^2+G_y^2}(模2)$$

$$G=max(|G_x|,|G_y|)(模\infty)$$

显然，梯度的模大的点，有很大可能是边缘点。常用的梯度算子有Roberts算子、Sobel算子和Prewitt算子。

Roberts算子

$$s_x=\left[\begin{array}{cc} 1&0\\ 0&-1\end{array} \right],s_y=\left[\begin{array}{cc} 0&-1\\ 1&0\end{array} \right]$$

$$G(i,j)=|s_x\otimes f|+|s_y\otimes f|$$

$$=|f(i,j)-f(i+1,j+1)|+|f(i+1,j)-f(i,j-1)|$$

以下将$s_x\otimes f$简记做$G_x$。

Sobel算子

$$s_x=\left[\begin{array}{ccc} -1&0&1\\ -2&0&2 \\ -1&0&1\end{array} \right],s_y=\left[\begin{array}{ccc} 1&2&1\\ 0&0&0 \\ -1&-2&-1\end{array} \right]$$

$$G=\sqrt{G_x^2+G_y^2}$$

$$梯度方向\theta=arctan(\frac{G_y}{G_x})$$

Prewitt算子

$$s_x=\left[\begin{array}{ccc} -1&0&1\\ -1&0&1 \\ -1&0&1\end{array} \right],s_y=\left[\begin{array}{ccc} 1&1&1\\ 0&0&0 \\ -1&-1&-1\end{array} \right]$$

其他与Sobel算子相同。

拉普拉斯算子

拉普拉斯算子是一种二阶微分算子，因此，它一般用二阶微分符号$\nabla^2f$来表示。其常用的相关核有：

$$h_1=\left[\begin{array}{ccc} 0&-1&0\\ -1&4&-1 \\ 0&-1&0\end{array} \right],h_2=\left[\begin{array}{ccc} -1&-1&-1\\ -1&8&-1 \\ -1&-1&-1\end{array} \right]$$

从中可以看出，拉普拉斯算子的相关核有以下特点：

1.各元素中心对称。

2.中心元素为正值。（在有些课本中，中心元素也可为负值，但相关公式就需要做相应的符号上的修改。在本教程中，中心元素一律为正值。）

3.所有元素的和为0。

拉普拉斯算子和正态分布有很大关联，也有标准差$\sigma$的概念。一般来说，中心元素的值越大，$\sigma$越小。算子对图像的模糊（或锐化）程度与$\sigma$成正比。

对称梯度算子

$$s_x=\left[\begin{array}{ccc} -1&0&1\\ -d&0&d \\ -1&0&1\end{array} \right],s_y=\left[\begin{array}{ccc} 1&d&1\\ 0&0&0 \\ -1&-d&-1\end{array} \right]$$

可以看出Sobel算子$(d=2)$和Prewitt算子$(d=1)$，都是对称梯度算子的特例。d的常用值还有$\sqrt{2}$。

波纹算子

$$s_x=\left[\begin{array}{ccc} 0&-1&d\\ 1&0&-1 \\ -d&1&0\end{array} \right],s_y=\left[\begin{array}{ccc} d&-1&0\\ -1&0&1 \\ 0&1&-d\end{array} \right]$$

对称梯度算子和波纹算子都属于边缘子空间基。

直线算子

$$s_x=\left[\begin{array}{ccc} 0&1&0\\ -1&0&-1 \\ 0&1&0\end{array} \right],s_y=\left[\begin{array}{ccc} -1&0&1\\ 0&0&0 \\ 1&0&-1\end{array} \right]$$

直线算子和拉普拉斯算子都属于直线子空间基。

边界闭合

如果像素$(s,t)$在像素$(x,y)$的领域，且满足以下条件：

$$|G(s,t)-G(x,y)|\le 幅度阀值T$$

$$|\theta(s,t)-\theta(x,y)|\le 角度阀值A$$

则可将像素$(s,t)$和像素$(x,y)$连接起来。

canny算法

Canny边缘检测算子是John F.Canny于1986年开发出来的一个多级边缘检测算法。

1.应用高斯滤波来平滑图像，目的是去除噪声。

2.找寻图像的强度梯度（intensity gradients)

3.应用非最大抑制（non-maximum suppression）技术来消除边误检（本来不是但检测出来是）。

4.应用双阈值的方法来决定可能的（潜在的）边界。

5.利用滞后技术来跟踪边界。

1、2的基本原理，上面已经讨论过了，这里不再赘述。

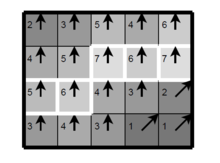
非最大抑制

图中的数字代表了像素点的梯度强度，箭头方向代表了梯度方向。以第二排第三个像素点为例，由于梯度方向向上，则将这一点的强度（7）与其上下两个像素点的强度（5和4）比较，由于这一点强度最大，则保留。

双阈值（Double Thresholding）

设定一个阈值上界和阈值下界，图像中的像素点如果大于阈值上界，则认为必然是边界（称为强边界，strong edge），小于阈值下界则认为必然不是边界，两者之间的，被认为是候选项（称为弱边界，weak edge）。

滞后的边界跟踪

和强边界相连的弱边界认为是边界，其他的弱边界则被抑制。

参考：

http://www.cse.iitd.ernet.in/~pkalra/csl783/canny.pdf

距离变换

距离变换(distance transform)是一种将二值图像灰度化的变换。

方法：

首先对图像进行二值化处理（这里的二值化通常是边缘检测后的结果），然后给每个像素赋值为离它最近的边界像素点与其的距离（Manhattan距离或欧氏距离），以得到distance metric(距离矩阵)，那么离边界越远的点越亮。

效果图：

这种效果通常叫做羽化效果。

常用的距离公式有：

$$\rho(r)=\frac{r^2}{2}$$

$$\rho(r)=r$$

$$\rho(r)=2\left(\sqrt{1+\frac{r^2}{2}}-1\right)$$

$$\rho(r)=C^2\left(\frac{r}{C}-log\left(1+\frac{r}{C}\right)\right),C=1.3998$$

$$\rho(r)=\frac{C^2}{2}\left[1-\exp\left(-\left(\frac{r}{C}\right)^2\right)\right],C=2.9846$$

马氏距离

Mahalanobis Distance是印度现代统计学之父Prasanta Chandra Mahalanobis于1936年提出的概念。

注：Prasanta Chandra Mahalanobis，1893~1972，印度统计学家，剑桥大学博士，印度统计研究所创始人。

印度的重点研究所一般叫做Institute of National Importance，共92所。Indian Statistical Institute是其中唯一一所和统计相关的研究所。教师255，学生375，这得是多精英的教育啊。其计算机科学专业排名印度第2。

p维空间的两点（两个p维向量x,y）的欧氏距离定义为：

$$d_E(x,y)=\sqrt{(x_1-y_1)^2+\dots+(x_p-y_p)^2}=\sqrt{(x-y)^T(x-y)}（公式1）$$

因此，x到原点的距离为：

$$\parallel x\parallel=d_E(x,0)=\sqrt{(x_1)^2+\dots+(x_p)^2}（公式2）$$

也就是：

$$x_1^2+\dots+x_p^2=\parallel x\parallel^2（公式3）$$

这实际上是个正球体的方程，也就是说观测数据x的各个分量对x至中心的欧氏距离贡献是相等的。然而在统计学中我们希望寻求这样一种距离，它的各个分量的作用程度是不同的。差别较大的分量应该接受较小的权重。

于是，公式3可变形为椭球体方程：

$$(\frac{x_1}{s_1})^2+\dots+(\frac{x_p}{s_p})^2=\parallel x\parallel^2（公式4）$$

其中的$s_i$表示i分量的权重。

公式4进一步整理，并扩展到两个p维向量x,y，可得马氏距离定义：

$$d_M(x,y)=\sqrt{(\frac{x_1-y_1}{s_1})^2+\dots+(\frac{x_p-y_p}{s_p})^2}=\sqrt{(x-y)^TD^{-1}(x-y)}（公式5）$$

其中，$D=diag(s_1^2,\dots,s_p^2)$。

注意：这里p维向量是正交基，否则的话，D将不是主对角线矩阵，而是一个普通的协方差矩阵。显然如果D为单位矩阵的话，马氏距离就变成了欧氏距离。

闵可夫斯基距离

Hermann Minkowski（1864-1909），德国数学家，哥廷根大学数学教授，爱因斯坦的老师。

Minkowski distance的定义：

$$d(x,y)=\sqrt[\lambda]{\sum_{i=1}^{n}\lvert x_i-y_i\lvert^{\lambda}}$$

显然，当$\lambda=2$时，该距离为欧氏距离。当$\lambda=1$时，也被称为CityBlock Distance或Manhattan Distance（曼哈顿距离）。

锐化

锐化是与模糊相反的图像操作，它的主要思想是增大图像色彩（或灰度）的对比度，简单的说就是：让亮的更亮，让暗的更暗。因此，锐化操作和边缘检测有很大的共同点，常用的锐化算法有梯度锐化和拉普拉斯锐化。

梯度锐化

$$g=\begin{cases} f+C, & G>T \\ f, & G\le T \\ \end{cases}$$

当像素$(x,y)$的梯度G大于阀值T时，在旧的像素值f上加上常数C，否则，保持原值。

拉普拉斯锐化

$$g=f+\nabla^2f$$

其中$\nabla^2f$表示f的二阶导数。

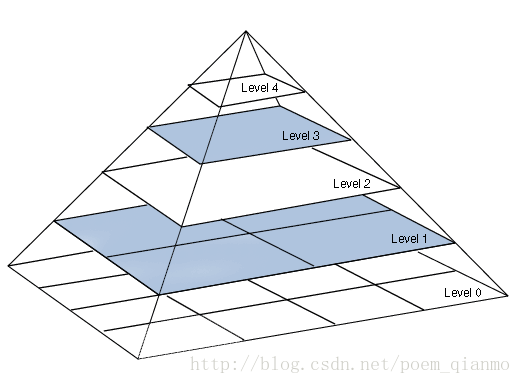
图像金字塔

一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低，且来源于同一张原始图的图像集合。

图像金字塔在机器视觉和图像压缩领域使用的比较多，比如OpenGL中的纹理处理。

图像金字塔有两种基本操作：

1.对图像向上采样：PyrUp——图像尺寸加倍。

2.对图像向下采样：PyrDown——图像尺寸减半。

这两种操作由于是针对图像尺寸而言的，因此，其方向和上图所示的金字塔的方向相反。

高斯金字塔

高斯金字塔是通过高斯平滑和亚采样获得一些列下采样图像，也就是说第K层高斯金字塔通过平滑、亚采样就可以获得K+1层高斯图像，高斯金字塔包含了一系列低通滤波器，其截至频率从上一层到下一层是以因子2逐渐增加，所以高斯金字塔可以跨越很大的频率范围。

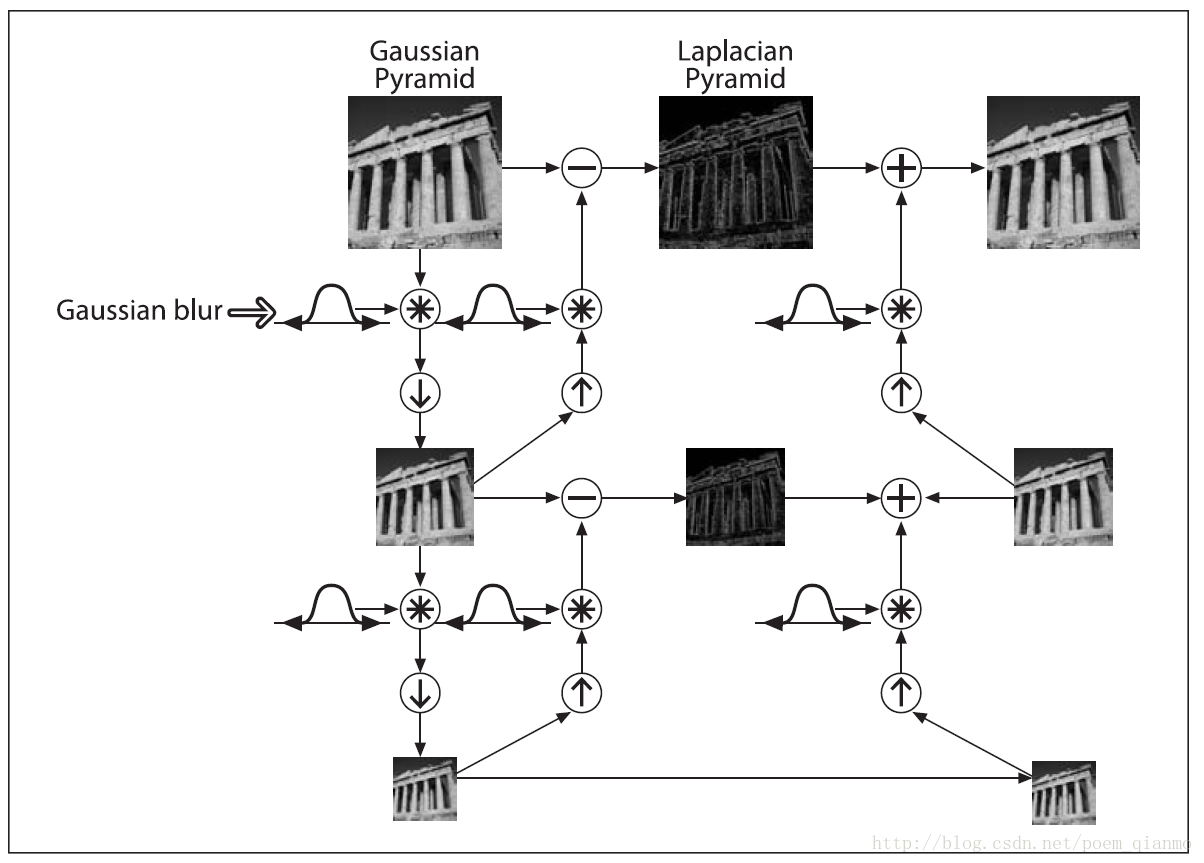
拉普拉斯金字塔

一般来说，由于PyrDown的过程会损失部分图像信息，因此通常情况下：

$$G_i\neq PyrUp(PyrDown(G_i))$$

为了使PyrUp和PyrDown可逆，这里引入拉普拉斯金字塔的概念。其定义如下：

$$L_i=G_i-PyrUp(G_{i+1})=G_i-Up(G_{i+1})\otimes H_{5x5}$$

其中UP操作是将源图像中位置为(x,y)的像素映射到目标图像的(2x+1,2y+1)位置，$H_{5x5}$表示5x5的高斯核。

整个拉普拉斯金字塔运算过程可以通过下图来概括：

图中最左列和最右列都是高斯金字塔，中间一列是拉普拉斯金字塔。

Steerable金字塔

将拉普拉斯金字塔中的高斯滤波函数，换成Steerable滤波函数即可。