8.6.8 矩阵变形方法

用户在代码中可以创建矩阵类的实例，并通过手动设置矩阵的内部属性a、b、c、d、tx和ty，纯手工的创造或改变一个变换矩阵。如果用户具备丰富的图形学知识，可以自己算出位移，缩放，旋转，斜切等变形所需要的二次变换矩阵值，那么使用这种方法就足够了。高级用户使用这种方式将会相当的高效。

但是，显然大多数用户并不了解矩阵数学和计算机图形学算法。对它们而言，直接操作Matrix类的属性是很不容易的。所以为了简化用户操作，AS3中的Matrix类绑定了一些内部方法。初级用户完全可以不顾及矩阵数学和图形学算法，通过使用这些内建的方法，修改它们的参数，累加它们的效果，最终得到想要的结果。

表所示为AS3中Matrix类内建的变形方法：

表Matrix类内建变形方法

名称	详情
translate(tx， ty)	实现显示对象的移动。 其中的tx，ty描述的是显示对象移动的差值，而不是目标点的最终坐标。
scale(sx， sy)	实现显示对象的放大和缩小。 sx：倍数，对应x坐标。 sy：倍数，对应y坐标。
rotate(q)	旋转一个对象 q：对象的旋转量。这是一个弧度值。

为了了解矩阵类的实际使用，下面介绍一个最简单的实例。新建AS3项目，在代码编辑器中直接输入以下代码：

var myMatrix:Matrix=new Matrix;

trace(myMatrix.toString());

 

//使用translate()方法修改矩阵

myMatrix.translate(5，13);

trace(myMatrix.toString());

 

//新建一个点

var myp:Point=new Point(5，5);

trace(myp.toString());

 

//新建一个目标点，用于接受位移后的坐标

var mypt:Point;

//应用位移矩阵

mypt=myMatrix.transformPoint(myp);

 

//输出目标点的坐标

trace(mypt.toString());

以上代码较为简单，注释也很清楚，不再赘述。运行这段代码，可以得到输出：

(a=1， b=0， c=0， d=1， tx=0， ty=0)//初始变换矩阵

(a=1， b=0， c=0， d=1， tx=5， ty=13)//修改后的变形矩阵

(x=5， y=5)//原坐标

(x=10， y=18)//目标坐标

至此，矩阵类的运行流程就很清楚了。声明一个矩阵类就建立了一个初始变换矩阵，初始矩阵如图所示：

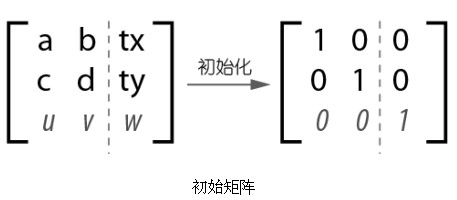
使用矩阵类的方法其本质是修改这个初始矩阵，应用矩阵类其实就是用该变形矩阵代入仿射变形公式进行运算的过程。

有的用户觉得这些方法使用起来并不方便，因为它们都是相对值。例如，其中的translate(tx，ty)方法，并不能将对象直接移动到目标点，其真实作用是在水平方向上移动tx距离，在垂直方向上移动ty距离。如果想把显示对象移动到某点，用户必须自己进行计算前后的距离差。

其实这是矩阵的内部机制造成的。Matrix类的这些方法都是基于矩阵操作的，遵循的是数学思维。当用户使用translate(tx，ty)方法时，本质上构建一个产生位移的数学矩阵。矩阵提供了一种仿射变形的映射。AS3执行时，将这个矩阵应用在显示对象内部的每一个点，令它们在水平方向上移动tx距离，在垂直方向上移动ty距离。假设能够指定最终的目标值，则运算后，显示对象的每一个点都会被映射到这同一个点，则显示对象就被扭曲压缩了，这显然是不正确的。

如果用户从人的思维去考虑，觉得这些内建方法不方便，可以自己写一组自定义函数，扩展它们的功能。