Normal Map的一些细节问题

最新推荐文章于 2024-04-27 09:31:17 发布

置顶 cywater2000

最新推荐文章于 2024-04-27 09:31:17 发布

阅读量8.6k

点赞数 5

分类专栏：游戏开发文章标签： float vector matrix reference orthogonal byte

本文链接：https://blog.csdn.net/cywater2000/article/details/749341

版权

游戏开发专栏收录该内容

29 篇文章 1 订阅

订阅专栏

Normal Map的一些细节问题

作者：cywater2000

出处： http://blog.csdn.net/cywater2000

日期：2006-5-22

转载请注明出处

1.Noraml Map的用处

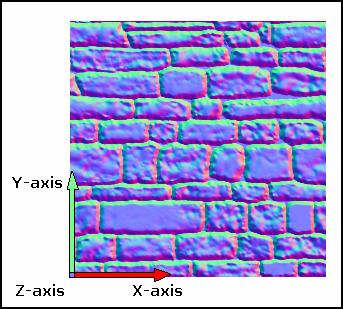
一是用在Bump Map中，表现粗糙或凹凸的表面。

（经典例子是桔子皮或者砖墙）

二是用在High Polygon Detail for Low Polygon，即用低多边形模型表现高多边形细节。

2.Normal Map的生成

(1)对于Bump Map，通常是由Height Map生成的。公式的前提是：square patch assumption,“this assumption is acceptable for many important surfaces such as flat polygons, spheres, tori, and surfaces of revolution.”因此基本上够用了。

N’ = N + D = [ 0,0, c ] + D = [ a ,b,c ]

a = -dF/du * 1/k

b = -dF/dv * 1/k

c = 1

通常 K取1。而偏导(partial differentials)用有限差分(finite differences)求。也可看成是图像处理中的“锐化滤波”。通常可用索伯尔(sobel filter)算子求(注意：通常边界不太好处理，但有各种解决办法)。

-1 0 1 1 2 1

dx = -2 0 2 dy = 0 0 0

-1 0 1 -1 -2 -1

注意结果要单位化，并且由于法线的范围是[-1, 1]，所以还要转换到颜色的范围[0, 1] (又即0~255)

例如：下面的代码来自于 ATI的TGAtoDOT3

for(y = 0; y < gHeight; y++)

{

for(x = 0; x < gWidth; x++)

{

// Do Y Sobel filter

ReadPixel(srcImage, &pix, (x-1+gWidth) % gWidth, (y+1) % gHeight);

dY = ((float) pix.red) / 255.0f * -1.0f;

ReadPixel(srcImage, &pix, x % gWidth, (y+1) % gHeight);

dY += ((float) pix.red) / 255.0f * -2.0f;

ReadPixel(srcImage, &pix, (x+1) % gWidth, (y+1) % gHeight);

dY += ((float) pix.red) / 255.0f * -1.0f;

ReadPixel(srcImage, &pix, (x-1+gWidth) % gWidth, (y-1+gHeight) % gHeight);

dY += ((float) pix.red) / 255.0f * 1.0f;

ReadPixel(srcImage, &pix, x % gWidth, (y-1+gHeight) % gHeight);

dY += ((float) pix.red) / 255.0f * 2.0f;

ReadPixel(srcImage, &pix, (x+1) % gWidth, (y-1+gHeight) % gHeight);

dY += ((float) pix.red) / 255.0f * 1.0f;

// Do X Sobel filter

ReadPixel(srcImage, &pix, (x-1+gWidth) % gWidth, (y-1+gHeight) % gHeight);

dX = ((float) pix.red) / 255.0f * -1.0f;

ReadPixel(srcImage, &pix, (x-1+gWidth) % gWidth, y % gHeight);

dX += ((float) pix.red) / 255.0f * -2.0f;

ReadPixel(srcImage, &pix, (x-1+gWidth) % gWidth, (y+1) % gHeight);

dX += ((float) pix.red) / 255.0f * -1.0f;

ReadPixel(srcImage, &pix, (x+1) % gWidth, (y-1+gHeight) % gHeight);

dX += ((float) pix.red) / 255.0f * 1.0f;

ReadPixel(srcImage, &pix, (x+1) % gWidth, y % gHeight);

dX += ((float) pix.red) / 255.0f * 2.0f;

ReadPixel(srcImage, &pix, (x+1) % gWidth, (y+1) % gHeight);

dX += ((float) pix.red) / 255.0f * 1.0f;

// Cross Product of components of gradient reduces to

nX = -dX;

nY = -dY;

nZ = 1;

// Normalize

oolen = 1.0f/((float) sqrt(nX*nX + nY*nY + nZ*nZ));

nX *= oolen;

nY *= oolen;

nZ *= oolen;

pix.red = (BYTE) PackFloatInByte(nX);

pix.green = (BYTE) PackFloatInByte(nY);

pix.blue = (BYTE) PackFloatInByte(nZ);

WritePixel(dstImage, &pix, x, y);

}

BYTE PackFloatInByte(float in)

{

return (BYTE) ((in+1.0f) / 2.0f * 255.0f);

}

注意 ATI在这里最后一行和一列用了WRAP的方法，即循环： % gWidth, % gHeight。

并且它是通过 red通道计算的，通常应该用户自己选择使用哪些参数。

例如： Photoshop plug-in from NVIDIA

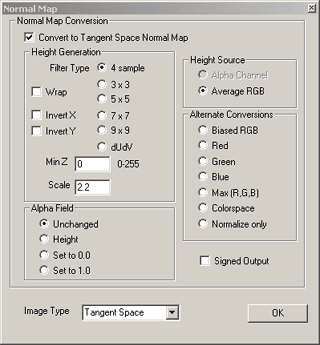
(2)对于High Poly Detail for Low Poly，则相对要复杂一些。(例如Z-Brush)

通常作法是先做低模，再刻高模（其实通常要在低模的基础上做一个中模），然后低模套高模，从低模的每个顶点作射线与高模求交，计算交点处的法线。

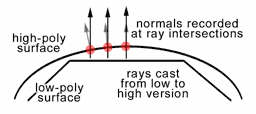
An even cooler use for a normal map is to make a low res model look almost exactly like a high res model. This type of normal map is generated by the computer instead of painted like a bump map. Here is how it works: First you create two versions of the model: a high polygon version (which can contain as much detail as you want) and a low polygon version that will actually get used in the game. Then you align the two models so that they occupy the same space and overlap each other.

Next you run a special program for generating the normal map. The program puts an empty texture map on the surface of the low res model. For each pixel of this empty texture map, the program casts a ray (draws a line) along surface normal of the low res model toward the high res model. At the point where that ray intersects with the surface of the high res model, the program finds the high res model normal. The idea is to figure out which direction the high res model surface is facing at that point and put that direction information (normal) in the texture map.

Once the program finds the normal from the high res model for the point, it encodes that normal into an RGB color and puts that color into the current pixel in the afore mentioned texture map. It repeats this process for all of the pixels in the texture map. When it`s done, you end up with a texture map that contains all of the normals calculated from the high res model. It`s ready to be applied to the low res model as a normal map. I抣l show you how to create this type of normal map in the second half of the tutorial.

3. TBN的计算

在数学中对 TBN的定义：对于双参数曲面P(u,v)：

T = normalize(dx/du, dy/du, dz/du)

N = T × normalize(dx/dv, dy/dv, dz/dv)

B = N × T

(Tangent space is just such a local coordinate system. The orthonormal basis for the tangent space is the normalized unperturbed surface normal Nn, the tangent vector Tn defined by normalizing dP/du, and the binormal Bn defined as Nn ×Tn. The orthonormal basis for a coordinate system is also sometimes

called the reference frame.)

而对于由三角形构成的 Mesh，TBN的计算有很多方法，最简单的即用方程解：

(D3DX提供了两个帮助函数：D3DXComputeTangentFrame, D3DXComputeTangentFrameEx)

由仿射坐标系算法： V = x*X + y*Y + O：

例如： V1 = c1*T + c2*B + O。将V1,V2,V3分别写成公式后相减得：

△ v2v1 = △c2c1_TT + △c2c1_B B

△ v3v1 = △c3c1_TT + △c3c1_B B

两个方程两个未知数，所以：

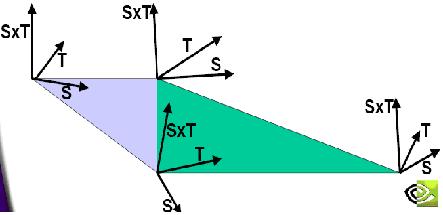
( 注意：上图是右手系，其中 S 即 Tangent ， T 即 Binormal)

问题 1 ：这样得到的 T 和 B 不一定正交 (orthogonal) 。是否需要通过： N = T X B, T = B X N( 若保留 B) 或 B = N X T( 若保留 T) 呢？

实际由于纹理坐标的映射通常是在正交的情况下作的 ( 平面的坐标基，又称为 reference frame) ，而 Normal Map 的映射与 Base Texture 的映射是一致的，所以可以认为 T 和 B 是正交的。当然，这种假设不一对，最好看情况而定。

问题2：顶点通常被多个三角形共享，是否应该“平均”TBN或者分割成单独的点？

查看D3D文档中关于 D3DXComputeTangentFrameEx 的说明时发现，对于共享点的情况是处理了的，通常要设一个阈值，如果共享点相邻三角形算出来的相差太大，则将共享点将分割成多个独立的点。

fPartialEdgeThreshold

[in] Specifies the maximum cosine of the angle at which two partial derivatives are deemed to be incompatible with each other . If the dot product of the direction of the two partial derivatives in adjacent triangles is less than or equal to this threshold, then the vertices shared between these triangles will be split .

同时还处理了“奇异点”：

fSingularPointThreshold

[in] Specifies the maximum magnitude of a partial derivative at which a vertex will be deemed singular. As multiple triangles are incident on a point that have nearby tangent frames, but altogether cancel each other out (such as at the top of a sphere) , the magnitude of the partial derivative will decrease. If the magnitude is less than or equal to this threshold, then the vertex will be split for every triangle that contains it.

甚至对于法线也同样：

fNormalEdgeThreshold

[in] Similar to fPartialEdgeThreshold, specifies the maximum cosine of the angle between two normals that is a threshold beyond which vertices shared between triangles will be split. If the dot product of the two normals is less than the threshold, the shared vertices will be split, forming a hard edge between neighboring triangles. If the dot product is more than the threshold, neighboring triangles will have their normals interpolated.

因此，实际上计算 TBN 要比想像中的复杂和麻烦。 ft

TBN的使用：

　 Tx Bx Nx

Lts = Los × Ty By Ny

Tz Bz Nz

即两个坐标系之间的转换 (object -> tangent)，原理可参考world space -> view space。由于光线L和半角H是矢量，所以第四行的平移量就不用了。

4.Self-Shadowing的解决

这里N是平面原有的法线(unperturbed normal)；N’是Normal Map中的perturbed normal

可以通过 (Lz< 0) ? 0 : 1来解决。但效果不太好: Simple, but may result in “hard” shadow boundary。Possible winking and popping of highlights。NVIDIA的同志(文献[2])提出了这样一个经验公式： min( 8*max(Lz,0), 1) 。

即：

Sself = min( 8*max(Lz,0), 1)。

I = Ia + Sself * ( Kd*max(0, L·N’) + Ks*max(0, N’·H) ^shininess )

5. 使用normalization cub map

由于要在VS中频繁地使用单位向量，而Normalize的花费比较大。所以通常使用预计算的normalization cub map来加速，即单位向量的查找表。

生成算法显然是: cube[x,y,z] = normalized(x, y, z)，不要忘了range-compress：[-1, 1] => [0, 1]

6. 纹理过滤对法线的影响及diffuse与specular计算时的一些区别

在文献[1]中提到：因为从 Normal Map中得到是经过纹理过滤后的扰动法线，所以它的结果并一定是单位化的。

但对于 diffuse的计算，它是恰当的：

Note that N’filtered is not generally normalized. Renormalizing N’filtered might seem reasonable and has been suggested in the literature [21], but not renormalizing when computing surface’s perceived diffuse intensity is actually more correct.

Note that if N’filtered is renormalized then bumpy diffuse surfaces incorrectly appear too bright. This result suggests that linear averaging of normalized perturbed normals is a reasonable filtering approach for the purpose of diffuse illumination. It also suggests that if bump maps are represented as perturbed normal maps then such normal maps can be reasonably filtered with conventional linear-mipmap-linear texturing hardware when used for diffuse lighting.

而对于specular的计算，则要求单位化。

由于以上两个原因，所以有一个技巧：

The single good thing about this approach is that there is an opportunity for sharing the same bump map encoding between the diffuse and specular illumination computations. The diffuse computation assumes an averaged perturbed normal that is not normalized while the specular computation requires the same normal normalized. Both needs are met by storing the normalized perturbed normal and a descaling factor. The specular computation uses the normalized normal directly while the diffuse computation uses the normalized normal but then fixes the diffuse illumination by multiplying by the descaling factor to get back to the unnormalized vector needed for computing the proper diffuse illumination.

A scaling factor for the normal. Mipmap level 0 has a constant magnitude of 1.0, but down-sampled mipmap levels keep track of the unnormalized vector sum length. For diffuse per-pixel lighting, it is preferable to make N` be the _unnormalized_ vector, but for specular lighting to work reasonably, the normal vector should be normalized. In the diffuse case, we can multiply by the "mag" to get the possibly shortened unnormalized length.

7. mipmap的使用

通常Normal Map也应该使用mipmap，因为如果base/decal texture使用了mipmap，而normal map不使用则显然对应不上。normal map的mipmap级应该和base texture一致。

而由于第6点提到的技巧，因此normal map的mipmap应该由程序手动实现，而不要让d3d或硬件自动创建，因为：自动创建并不会单位化，且通常我们还要在 alpha 通道里存法线的长度 ( 给 diffuse 用 )。

不过测试中发现，自动创建效果还可以接受。只是alpha通道没有意义了。