径向基函数(RBF)在神经网络领域扮演着重要的角色,如RBF神经网络具有唯一最佳逼近的特性,径向基作为核函数在SVM中能将输入样本映射到高维特征空间,解决一些原本线性不可分的问题。
本文主要讨论:
1. 先讨论核函数是如何把数据映射到高维空间的,然后引入径向基函数作核函数,并特别说明高斯径向基函数的几何意义,以及它作为核函数时为什么能把数据映射到无限维空间。
2.提到了径向基函数,就继续讨论下径向基函数神经网络为什么能用来逼近。
再看这文章的时候,注意核函数是一回事,径向基函数是另一回事。核函数表示的是高维空间里由于向量内积而计算出来的一个函数表达式(后面将见到)。而径向基函数是一类函数,径向基函数是一个它的值(y)只依赖于变量(x)距原点距离的函数,即  ;也可以是距其他某个中心点的距离,即
;也可以是距其他某个中心点的距离,即  . 引用自wiki . 也就是说,可以选定径向基函数来当核函数,譬如SVM里一般都用高斯径向基作为核函数,但是核函数不一定要选择径向基这一类函数。如果感觉这段话有点绕没关系,往下看就能慢慢体会了。
. 引用自wiki . 也就是说,可以选定径向基函数来当核函数,譬如SVM里一般都用高斯径向基作为核函数,但是核函数不一定要选择径向基这一类函数。如果感觉这段话有点绕没关系,往下看就能慢慢体会了。
为什么要将核函数和RBF神经网络放在一起,是希望学习它们的时候即能看到它们的联系又能找到其差别。
一.由非线性映射引入核函数概念,之后介绍高斯径向基及其几何意义。
预先规定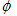
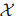
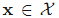
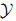
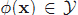
下面先用一个例子说明这种映射的好处。
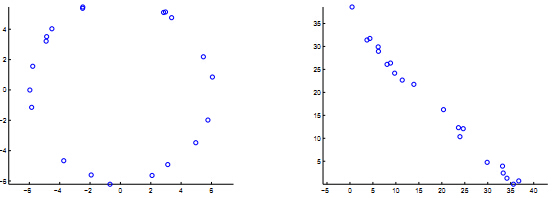
例:假设二维平面上有一些系列样本点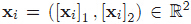
如果设非线性映射为:
那么在映射后的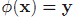
这意味着在新空间里,样本点是分布在一条近似直线上的,而不是之前的圆,很明显这是有利于我们的。
图1.左图为原来的x所在的二维空间,右图为映射后的新的y空间
继续这个例子,我们已经知道了映射关系,那么在y空间中的向量内积会是什么样子的呢?
注意公式里的各种括号。[x]代表样本x,圆括号(,)表示样本的坐标,尖括号<,>代表代表向量内积。
由此我们知道y空间里两向量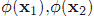
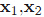
所以总结一下核函数就是:在原样本空间中非线性问题,我们希望通过一种映射把他映射到高维空间里使问题变得线性。然后在高维空间里使用我们的算法就能解决问题。当然这里按照前面的推导我们在高维空间里的运算是以向量内积为基础的。
回顾SVM里的应用得到的分类器表达式为:
把x经过映射后得到的表达式为:
由此就可以看到这里有高维空间里的内积,就能够用核函数代替这种内积了,而往往把高斯径向基函数作为核函数。
高斯径向基函数公式如下:
那么它有什么几何意义呢。
先看看x经过映射以后,在高维空间里这个点到原点的距离公式:
这表明样本x映射到高维空间后,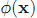
接下来将讨论核函数为什么能映射到高维空间,径向基核又为什么能够映射到无限维空间。
先考虑普通的多项式核函数:
![]() ,其中
,其中![]() ,并且
,并且 ![]() .
.
因此这个多项式核函数能够写成:
![]()
![]() .
.
现在回到之前的映射
![]()
并取 ![]() ,注意此时是3维空间了,那么有
,注意此时是3维空间了,那么有
![]() .
.
这就是前面的k(x,y),因此,该核函数就将2维映射到了3维空间。
看完了普通核函数由2维向3维的映射,再来看看高斯径向基函数会把2维平面上一点映射到多少维。
![]()
![]()
![]()
![]()
呃,看看它的泰勒展开式你就会恍然大悟:

这个时候 ![]() (x)就是一个无限维的了。
(x)就是一个无限维的了。
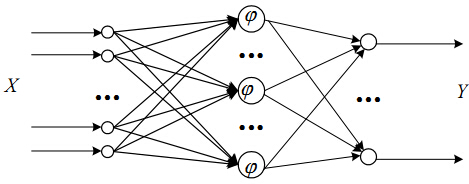
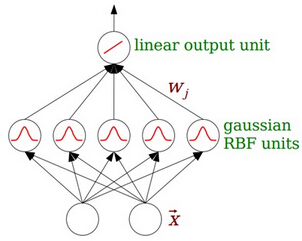
二、RBF神经网络
最基本的径向基函数(RBF)神经网络的构成包括三层,其中每一层都有着完全不同的作用。输入层由一些感知单元组成,它们将网络与外界环境连接起来;第二层是网络中仅有的一个隐层,它的作用是从输入空间到隐层空间之间进行非线性变换,在大多数情况下,隐层空间有较高的维数;输出层是线性的,它为作用于输入层的激活模式提供响应。
函数逼近的形式:
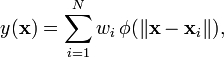
个人觉得,隐含层的每个节点就是就是空间中的一个基底,经过线性组合加权以后就变成了输出。这种理解是通过逼近理论来理解的。
这里的多项式P就是由基底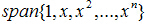
隐含层每个节点对应的响应输出就像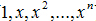
第二角度理解:
不知大家是否熟悉混合高斯模型,这里的逼近有点像混合高斯模型。也就是每个高斯函数在自己的中心附近作出突出贡献。
在这里推介zouxy09的博文《径向基网络(RBF network)之BP监督训练》,他的文章演示的比较清楚。我摘抄如下:
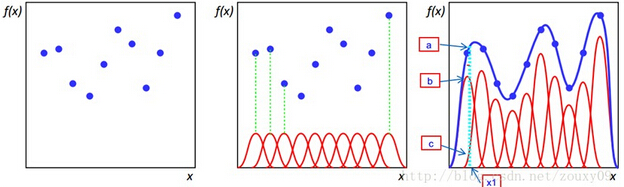
当年径向基函数的诞生主要是为了解决多变量插值的问题。可以看下面的图。具体的话是先在每个样本上面放一个基函数,图中每个蓝色的点是一个样本,然后中间那个图中绿色虚线对应的,就表示的是每个训练样本对应一个高斯函数(高斯函数中心就是样本点)。然后假设真实的拟合这些训练数据的曲线是蓝色的那根(最右边的图),如果我们有一个新的数据x1,我们想知道它对应的f(x1)是多少,也就是a点的纵坐标是多少。那么由图可以看到,a点的纵坐标等于b点的纵坐标加上c点的纵坐标。而b的纵坐标是第一个样本点的高斯函数的值乘以一个大点权值得到的,c的纵坐标是第二个样本点的高斯函数的值乘以另一个小点的权值得到。而其他样本点的权值全是0,因为我们要插值的点x1在第一和第二个样本点之间,远离其他的样本点,那么插值影响最大的就是离得近的点,离的远的就没什么贡献了。所以x1点的函数值由附近的b和c两个点就可以确定了。拓展到任意的新的x,这些红色的高斯函数乘以一个权值后再在对应的x地方加起来,就可以完美的拟合真实的函数曲线了。
我个人比较倾向径向基神经网络是把输入的样本映射到了另一个空间,在另一个空间经过线性组合后形成输出,得到逼近的结果,这种理解也有利于去窥探神经网络的本质。个人愚见,有错请指出。
(转载请注明作者和出处:http://blog.csdn.net/heyijia0327 未经允许请勿用于商业用途)
reference:
1.Michael Eigensatz《Insights into the Geometry of the Gaussian Kernel and an Application in Geometric Modeling》
2.Quora 上的问题 Why does the RBF (radial basis function) kernel map into infinite dimensional space?
3.zouxy09 博文《径向基网络(RBF network)之BP监督训练》
4.如果想学SVM, JerryLead 的 《支持向量机》系列 当然不能漏掉.
5.男神 Andrew Ng 的讲义是师祖.








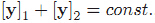
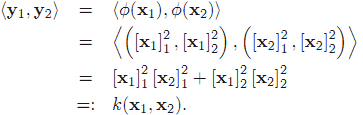
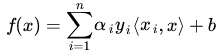
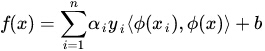
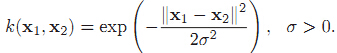
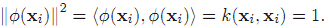















 1381
1381

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








