在上一部分中通过一个例子大致了解了graph based slam的优化过程。在本篇博客中将提升一个层次,对图优化的求解过程进行推导。由于博文关注的在图构建好以后,如何调整机器人位姿使误差最下。因此,本文主要涉及的是图优化的后端(back-end)。
我们已经知道图优化问题转变成了一个最小二乘问题。根据上篇博客最后一个例子,求机器人SLAM过程中最优轨迹可以表示成求解机器人位姿使得下面误差平方函数最小。
其中,表示图顶点的参数向量,如机器人位姿。
表示测量值,
表示该误差所占权重的矩阵。
是一个向量误差函数表示
和
之间的关系与测量
之间有多吻合。后面为了简化,将误差函数写成下面的形式:
下图为图优化的一个简单例子
对于上述最小二乘问题还可以从最大似然的角度解释。这里也作简单介绍,主要是为了更进一步的理解误差的权重矩阵。对于传感器的测量,我们可以假设它受高斯白噪声的影响。所以每一个测量值的分布可以看作是以真值为中心的高斯分布。如果测量是多变量的,那就是多元高斯分布。
多元高斯分布的协方差矩阵的某一维越大,高斯曲线越矮胖,表示在这个方向上越不确定。并且高斯分布中,均值部位概率最大。所以,对于某个测量,我们应该使它出现在概率最大的地方,这就是最大似然概率。可以得到似然概率的log形式的计算公式:
上式和前面的误差平方和函数很像,只不过这里显式的指明了误差函数的形式。所以我们发现,误差的权重矩阵(正式名称为信息矩阵)等于协防差矩阵的逆。由于图优化里每一条边代表一个测量值,如表示相邻位姿关系的编码器测量值或者图像(激光)匹配得到的位姿变换矩阵。所以图优化里每一条边的信息矩阵就是这些测量协防差矩阵的逆。如果协防差越小,表示这次测量越准越值得相信,信息权重就越大。
我们看到图优化问题变成了求解最小二乘问题,然而机器人位姿之间的变化函数不是线性的,所以是个非线性最小二乘问题,得通过迭代法进行求解。如果迭代开始时有一个好的初始假设值,那我们就能用Guass-Newton法或者 Levenberg-Marquardt法了。
假设我们已经有了好的初始假设值,需要在这个值附近迭代寻求最优解。求解的方法是把误差函数在该初始值附近进行一节泰勒展开
其中是误差函数
在
附近的雅克比矩阵。并且为了书写方便,使用
代替了
。
将上面的(5)式代入误差平方和中的某一项可以得到
将(10)式代入,可以重写误差平方和函数如下:
其中。为了求解上式,使得其最小,还是求其一阶导数并使其等于0,可以得
其中H是系统的信息矩阵(注意与边的信息矩阵区分),系统的解就是在初始值上叠加这个增量
Guass-Newton迭代法就是不断重复这个过程直到收敛。LM法引入了一个松弛因子来控制迭代速度:
然而,一个值得注意的问题是,上面的步进迭代是用的两个向量直接相加,这是在欧式空间中的做法。而机器人SLAM问题中涉及到平移和旋转,平移是在欧氏空间中,可是旋转就是在非欧空间了。在航迹推演的公式中我们也能看到相邻时刻间位姿的递增由于航向角的存在已经不是简单的相加了。所以得重新定义一个非线性算子来代表增量。
将这个非线性算子用在移动机器人相邻时刻的航迹推演,能够得到:
这里可能有点抽象,别急,在后面2d slam的图优化例子中将具体介绍。
上面的求解过程看起来简单,计算b,H,然后计算增量迭代直到收敛。然而,实际计算的时候,b,H,雅克比矩阵到底是啥得弄清楚。接下来,具体解析它们的结构。
误差函数只和
、
有关,因此它的雅克比矩阵和
、
无关的列都为0,有如下结构:
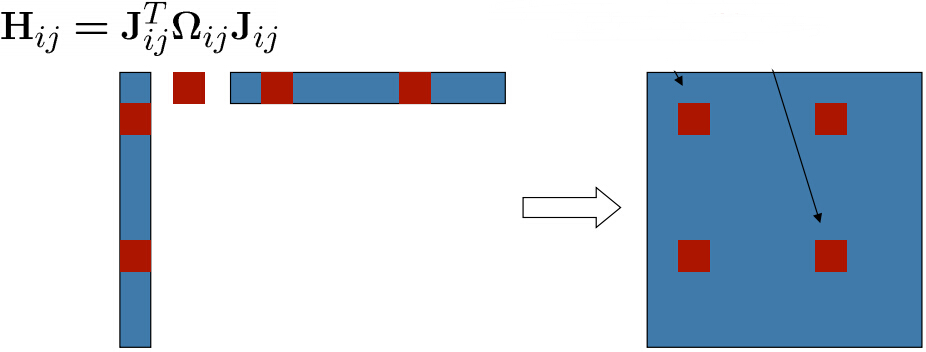
清楚了雅克比矩阵的结构,再来看b和H。我们已经知道是列向量,可以推算出结构如下,注意下图中
和
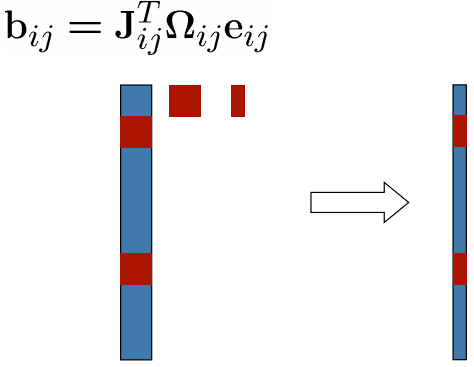
下面的色块代表矩阵和列向量,并且蓝色块代表0,红色块非0。可以看到只有和
、
有关的区域非零。
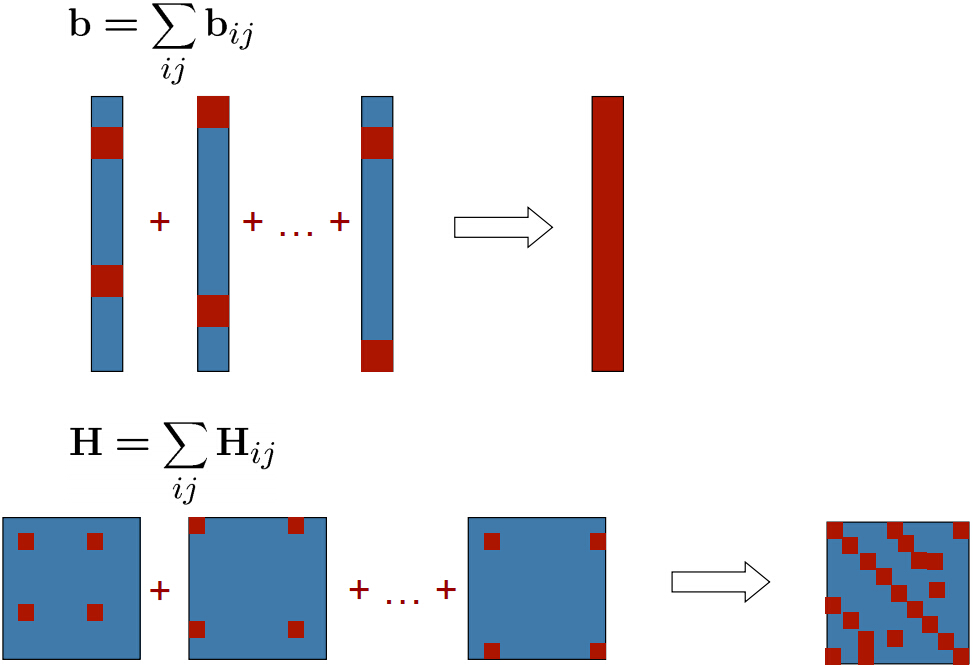
从上图中可以看出系统是稀疏的,并且正如上面图中的累加一样,程序中也可以对特定的ij计算相应的Hij,bij,然后再把所有的Hij,bij累加起来就行了。
最后把整个求解过程总结如下:
本篇博文对图优化后端(back-end)进行了推导,但是还有很重要的问题,雅克比矩阵在实际编程中如何计算?前面看到了针对非欧空间的递增设计了非线性算子,那么针对非欧空间的误差函数又该如何设计哩(不能直接两个向量相减求模了)?在下一篇博文中,将结合一个二维平面上的图优化例子进行讲解,同时配有matlab仿真代码。
(转载请注明作者和出处:http://blog.csdn.net/heyijia0327 未经允许请勿用于商业用途)
reference:
1. Grisetti. 《A Tutorial on Graph-Based SLAM》
2. Grisetti. 课件 《SLAM Back-end》(可以直接搜到)
3. Rainer & Grisetti 《g2o: A General Framework for Graph Optimization》





 本文深入探讨了图优化SLAM的后端求解过程,详细介绍了如何将SLAM问题转化为最小二乘问题,并通过迭代法求解最优机器人位姿。文章还讨论了非线性最小二乘问题的求解方法,包括Guass-Newton法和Levenberg-Marquardt法。
本文深入探讨了图优化SLAM的后端求解过程,详细介绍了如何将SLAM问题转化为最小二乘问题,并通过迭代法求解最优机器人位姿。文章还讨论了非线性最小二乘问题的求解方法,包括Guass-Newton法和Levenberg-Marquardt法。
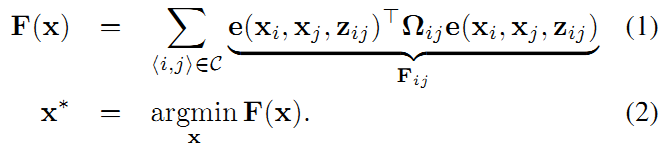
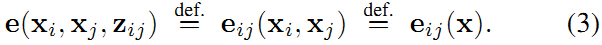
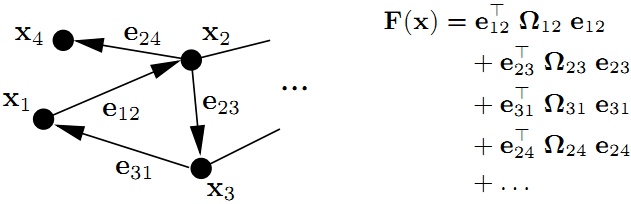
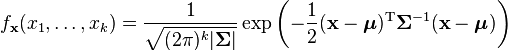
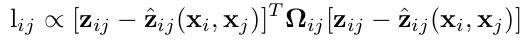
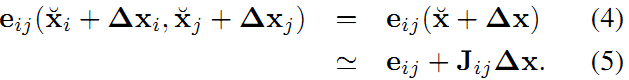
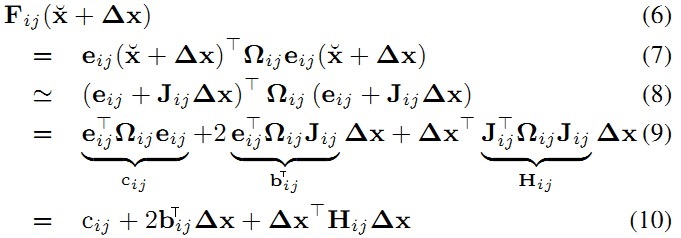
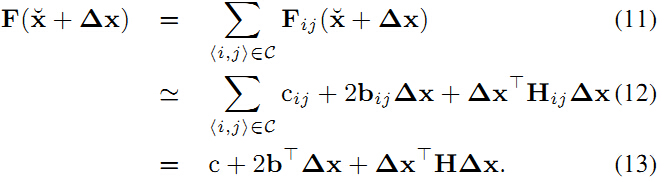

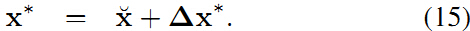
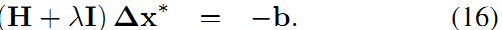
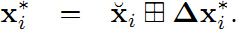
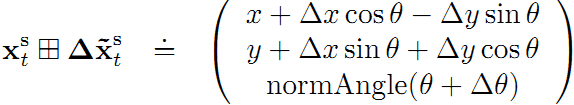

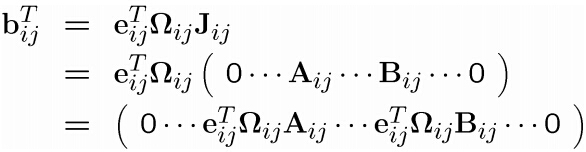
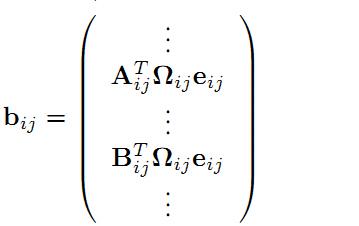
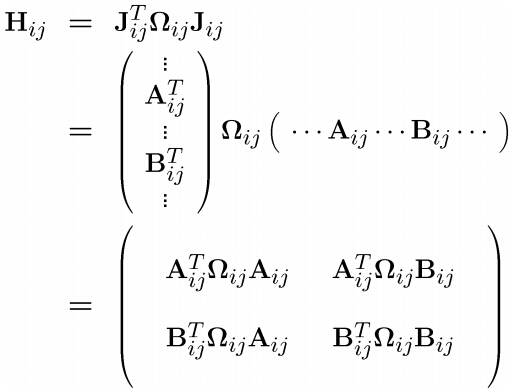

















 3万+
3万+










