【矩阵论】11——Jordan标准型——线性变换的特征值与特征向量

本系列文章由Titus_1996 原创，转载请注明出处。  

文章链接：https://blog.csdn.net/Titus_1996/article/details/83177254

本系列文章使用的教材为《矩阵论》（第二版），杨明，刘先忠编，华中科技大学出版社。

---

定义

假设T在某组基{α1，α2，...αn}下的矩阵为A，ξ是T关于λ的特征向量。则有

ξ=(α1，α2，...αn)X

对上式左右两边做线性变换，得到

T(ξ)=(α1，α2，...αn)AX

又因为T(ξ)=λξ=λ(α1，α2，...αn)X=(α1，α2，...αn)λX，对比可知AX=λX。这就有了以下定理：

总结：

• 在特定基下的T的矩阵的特征值就是线性变换T的特征值。

• 而T的特征向量为基与A特征向量的乘积。

• 特征值是由T本身决定的，与基和矩阵的选择无关。

---

线性变换特征值和特征向量的计算步骤：

1. 选择一组特定基，求对应矩阵A

2. 解|λE-A|=0，求λ

3. 将λ分别带回(λE-A)X=0,求特征向量。

其实这个步骤就是线性代数中求矩阵的特征值与特征向量的步骤，只不过这里矩阵的特征值是线性变换的特征值，而特征向量却不是。

---

下面讨论线性变换T的特征向量的性质

特征子空间

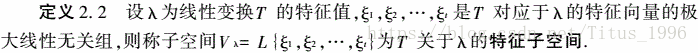
每一个特征值对应一个特征子空间。

注意：并不是所有特征子空间中的向量都是λ对应的特征向量。必须减去零向量，Vλ-{0}，因为特征向量是非零的。而在第一章讲到子空间中是包含零元的。所以必须减去零元。