在使用 OpenGL 的应用程序中,当我们指定了模型的顶点后,顶点依次会变换到不同的 OpenGL 空间中,最后才会被显示到屏幕上。在变换的过程中,通过使用矩阵,我们更高效地来完成这些变换工作。
本篇博客主要介绍的是矩阵以及矩阵在空间几何中的应用。关于 OpenGL 空间,我把它们安排在了另一篇博客OpenGL 的空间变换(下):空间变换中来介绍。
本篇博客主要分为两部分:矩阵基础和矩阵在空间几何中的应用。对熟悉矩阵的读者来说,可以跳过矩阵基础直接阅读第二部分。
矩阵基础
数学上,一个 mxn 的矩阵是一个由 m 行 n 列元素排列成的矩形阵列。矩阵里的元素可以是数字、符号或者数学式。例如下面是一个由 6 个数字构成的 2 行 3 列矩阵:
对于行(列)数为 1 的矩阵,我们称为行(列)向量。注意,这里的向量与空间几何中的向量并不是同一个概念。为了更好地区分两者,接下来只要描述的是矩阵的向量,本文都会以行(列)向量来表示。否则,描述的就是空间几何中的向量。
矩阵的基本运算
矩阵最基本的运算包括加(减)法、数乘和转置运算。
加(减)法:mxn 矩阵 A 和 B 的和(差):A±B 为一个 mxn 矩阵,其中每个元素是 A 和 B 相应元素的和(差)。
根据加(减)法我们还可以推导出,矩阵的取负操作实则是对每个元素进行取负操作。
数乘:标量 c 与矩阵 A 的数乘:c·A 的每个元素是 A 的相应元素与 c 的乘积。
转置:mxn 矩阵 A 的转置是一个 nxm 的矩阵,记为 A‘,其中的第 i 行第 j 列元素是原矩阵 A 的第 j 行第 i 列元素。
矩阵乘法
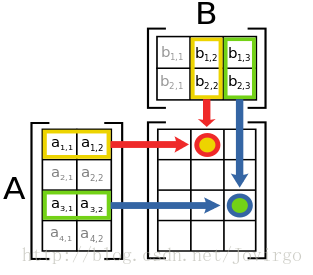
与矩阵的数乘不同,矩阵的乘法是指两个矩阵相乘,并且当且仅当在第一个矩阵 A 的列数与另一个矩阵 B 的行数相等时才有定义。假设 A 为 mxn 矩阵,而 B 是 nxp 矩阵,那么 A 乘以 B 的乘积 A·B 则是个 m x p 的矩阵。它的任意元素为:
其中, 其中1 ≤ i ≤ m, 1 ≤ j ≤ p。
通过下面这张示意图,我们可以更好地理解 A·B 的过程:
矩阵的乘法满足结合律和对矩阵加法的分配律(左分配律和右分配律):
结合律:(A·B)·C = A·(B·C)
左分配律:(A+B)·C = A·C+B·C
右分配律:C·(A+B








 这篇博客介绍了矩阵在空间几何中的应用,特别是如何使用矩阵进行平移、旋转和缩放变换。矩阵基础部分阐述了矩阵的基本运算,包括加法、数乘和转置。在空间几何中,矩阵用于表示三维空间的对象和变换,通过齐次坐标解决了描述无穷远点的问题。平移、旋转和缩放变换的矩阵表达式也详细给出,揭示了矩阵在描述几何变换中的重要角色。
这篇博客介绍了矩阵在空间几何中的应用,特别是如何使用矩阵进行平移、旋转和缩放变换。矩阵基础部分阐述了矩阵的基本运算,包括加法、数乘和转置。在空间几何中,矩阵用于表示三维空间的对象和变换,通过齐次坐标解决了描述无穷远点的问题。平移、旋转和缩放变换的矩阵表达式也详细给出,揭示了矩阵在描述几何变换中的重要角色。
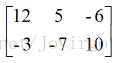
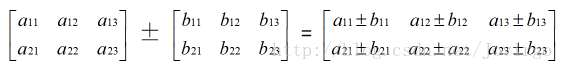
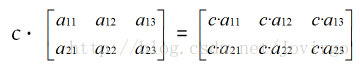

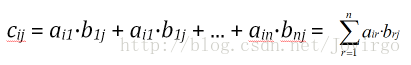
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1757
1757

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








