【机器学习详解】线性回归、梯度下降、最小二乘的几何和概率解释

线性回归

即线性拟合，给定N个样本数据$（x_1,y_1）,(x_2,y_2)....(x_N,y_N)$其中$x_i$为输入向量，$y_i$表示目标值，即想要预测的值。采用曲线拟合方式，找到最佳的函数曲线来逼近原始数据。通过使得代价函数最小来决定函数参数值。
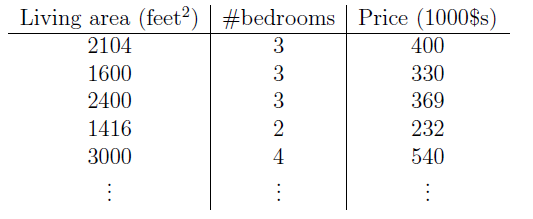
采用斯坦福大学公开课的例子：假如一套房子的价格只考虑由房屋面积(Living area)与卧室数目(bedrooms)两个因素决定，现在拿到手有m个样本，如下图所示。此例中，输入$x=(x_1,x_2)$为2维向量，分别对应房屋面积和卧室数目,$y$对应价格。现在想根据上述样本数据，预测新的输入$x^{(k)}$对应的$y^{(k)}$。

我们采用$x$的线性函数$h_θ(x)=θ_0+θ_1x_1+θ_2x_2$来近似$y$值，其中$θ_0$为偏移量。令$x_0=1$,简写为$h_θ(x)=θ^Tx$。现在的问题是如何选择$θ$的值，来使得$h_θ(x^{(i)})$最大程度接近$y^{(i)}$值。

最小二乘代价函数

采用最小二乘法定义代价函数$J(θ)=\frac12∑_{i=1}^m(h_θ(x^{(i)})−y^{(i)})^2$,表示每个样本的预测值与真实值得差值平方的累加和。
现在问题转化为代价函数$J(θ)$最小对应的$θ$值，其中因子$\frac12$是为了后面的计算方便。

梯度下降：

梯度下降的思想是沿着函数负梯度方向，不断更新$θ$值，每次更新一次，函数值下降一次，算法如下：

1.初始化$θ$值；
2.更新$θ$值，使得$J(θ)$值更小 ：$θ:=θ−α∇_θJ(θ)$；
3.如果$J(θ)$值可以继续减少，返回第2步；

其中$α$称为学习率，决定着每一次迭代跨越的步长。$θ^T=(θ_0,θ_1,θ_2)$为一个三维向量，梯度偏导数计算方法：

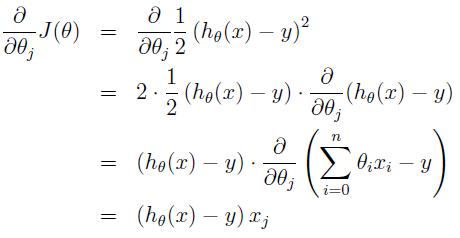
对于单个样本数据，则更新方法为$θ_j:=θ_j−α(h_θ(x)−y)x_j$

关于梯度下降与梯度上升：
注意到，我们上述求偏导数得到$(h_θ(x)−y)x_j$，此方向为梯度上升方法，由于我们要求$J(θ)$的最小值，所以应沿着负梯度方向，即$θ_j:=θ_j−α(h_θ(x)−y)x_j$，若提取负号，就变为$θj:=θj+α(y−h_θ(x))x_j$,虽然变为正号，仍然是沿着负梯度方向，只是公式形式变了。在《机器学习实战》中，就采用的后一种形式$θ_j:=θ_j+α(y−h_θ(x))x_j$，在那本书里被称为梯度上升，实际上仍然为负梯度方向。

1.批梯度下降(batch gradient descent)

上述为批梯度下降$θ$值得更新算法，每一次更新$θ$值，都需要计算整个样本集数据，即综合全局梯度方向算出下一步最优梯度方向。在学习率$α$比较小的情况下，上述算法必定收敛，同时由于$J(θ)$为凸二次函数，局部最优值，即全局最优值。
但是对于样本集非常大的情况下，此种算法必然导致效率很低，因为每一次对$θ$的更新，都需计算每个样本的预测值与真实值的差。

2.随机梯度下降（stochastic gradient descent）

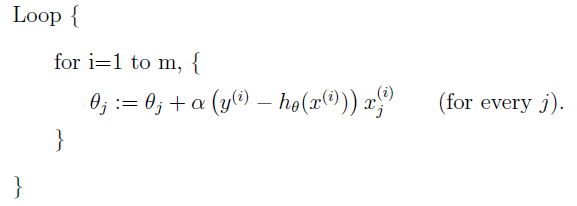
算法的优点是，遍历整个数据集，每一次更新$θ$的值只计算单个样本数据的梯度方向。但是此种算法不一定收敛到最小值，可能会在最小值附近震荡，在数据量很大的情况下，仍建议采用随机梯度下降算法。
3.mini-batch梯度下降
把批梯度下降与随机梯度下降算法折中，即每次采用若干样本的梯度综合，更新$θ$的值，被称为mini-batch梯度下降。
$θ_j=θ_j+α∑_n(y^{(i)}−h_θ(x^{(i)}))$(for every j)

解析式求解

改写$J(θ)$成矩阵的形式：
$J(θ)=\frac12∑_{i=1}^m(h_θ(x^{(i)})−y^{(i)})^2=\frac12(Xθ−Y)^T(Xθ−Y)$，其中X为m×n,$θ$为n×1，$Y=(y^{(1)},y^{(2)}...y^{(m)})^T$
令$∇_θJ(θ)=∇θ\frac12(θ^TX^TXθ−θ^TX^TY−Y^TXθ+Y^TY)=\frac12(2X^TXθ−2X^TY)=X^TXθ−X^TY=0$
解得$θ=(X^TX)^{−1}X^TY$;
当$X^TX$为奇异矩阵时，通常选择在原始函数中添加正则项，确保矩阵非奇异。
一种简单的正则化项为：$E(θ)=\frac12θ^Tθ$, 原始目表函数变为$J(θ)+λE(θ)=\frac12∑^m_{i=1}(h_θ(x^{(i)})−y^{(i)})^2+\fracλ2θ^Tθ$,其中$λ$为调和因子,对目标函数求导并令为0，解得$θ=(X^TX+λI)^{−1}X^TY$

最小二乘法的概率解释与几何解释

1.概率解释

假定原始拟合函数为：$y^{(i)}=θ^Tx^{(i)}+ϵ^{(i)}$，即每个样本受到一个噪声$ϵ^{(i)}$因子的影响，同时噪声分别服从正态高斯分布，即均值为0，方差为$σ^2$。
$ϵ(i)$~$N(0,σ^2)$
$\Longrightarrow P(ϵ^{(i)})=\frac1{\sqrt{2π}σ}exp(−\frac{(ϵ^{(i)})^2}{2σ^2})$
$\Longrightarrow P(y^{(i)}|x^{(i)};θ)=\frac1{\sqrt{2π}σ}exp(−\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2σ^2})$
写法$P(y^{(i)}|x^{(i)};θ)$表示在参数$θ$的情况下，给定$x^{(i)}，y^{(i)}$服从的分布。
由于假定噪声因子之间$ϵ^{(i)}$为独立同分布，写出其似然函数为，现在的目的是采用最大释然估计得方法计算出最优的参数$θ$值

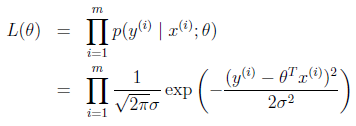
改成对数释然函数为：

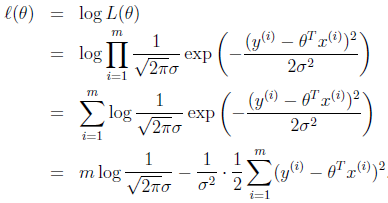
我们目的要最大化释然函数，即要求最小化第二项 $\frac12∑^m_{i=1}(h_θ(x^{(i)})−y(i))^2$，此即我们的最小二乘的方法。
采用最小二乘的方法作为优化目标即潜在的使用了最大释然估计的方法。

2.几何解释

下面从几何角度解释最小二乘法的原理:为了结合下面的图形解释，需要改变一下数据的表示方法。假定样本量的数目为$N$，样本i记为$(x_i,t_i)$，且样本特征xi的维数为$M$,$M<N$。
1.所有样本目标真实值$t_i$，构成一个N维列向量$t=(t_1,t_2...t_N)^T$;
2.所有样本的特征数据x构成一个N×M的矩阵X;矩阵X的第j个列向量记维$φ_j$，即$X=(φ_0,φ_1,...,φ_{M−1})$
3.假定真实最优参数为$θ^∗=(θ_0,θ_1,...θ_{M−1})^T$,则有$t=Xθ^∗=(φ_0,φ_1,...,φ_{M−1})θ^∗$

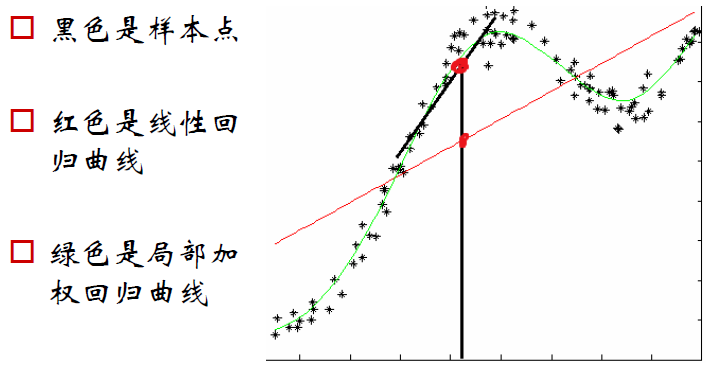
我们的目的是寻找最好的拟合参数$θ$，使得拟合出的预测值$y=Xθ=(φ_0,φ_1,...,φ_{M−1})θ$离真实值向量$t$最近，注意到$X$是样本数据，是固定值，每一列的$φ_i$即相当于$M$维空间的一个基向量。$(φ_0,φ_1,...,φ_{M−1})$,即构成了$M$维子空间的一组基向量，记做子空间$S$。子空间$S$中任何向量都可以通过基向量的线性组合表示。最小二乘法在几何上解释，即寻找一个向量$y$与向量$t$之间欧式距离最小。现在的目的即是在$S$中寻找一个向量$y$,使得$y$离向量$t$的距离最近。最由图中可以看出，离$t$最近的向量$y$即是向量$t$向子空间$S$的正交投影。

局部加权回归（LWR）

LWR算法是非参数模型的一种，因为每一次预测新的数据，都需要采用原始样本计算一次，必然降低了效率。线性回归算法属于参数模型的一种，当得到最优参数$θ$,预测新的数据时，就不需要原始数据样本了。
最小二乘法的目标(代价)函数是$J(θ)=\frac12∑^m_{i=1}(h_θ(x^{(i)})−y(i))^2$，它采用了总体样本数据的性质，来预测新的数据,即所以样本的权重相同，不考虑局部性质。它的缺点是若原始数据分布由多个模型函数共同产生，采用最小二乘法的原则并不能最佳地逼近原始数据形态。而局部加权回归通过增大预测的数据$x^{(i)}$附近的样本点的权重，较小相对较远的样本数据的权重，来预测输出值$h(x^{(i)})$。
局部加权回归算法：

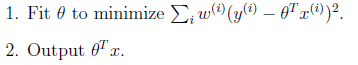
其中ω(i)为第i个样本的权重
一种常用的权重分布函数为，类似高斯分布曲线：

参数τ控制偏离预测点距离权重的下降幅度。

参考：机器学习公开课—Andrew Ng