转载请注明出处http://blog.csdn.net/luoshixian099/article/details/51028244
1.概率生成模型
首先介绍生成模型的概念,然后逐步介绍采用生成模型的步骤。
1.1概念
即对每一种类别 Ck 分别建立一种数据模型 p(x|Ck) ,把待分类数据x分别带入每种模型中,计算后验概率 p(Ck|x) ,选择最大的后验概率对应的类别。
假设原始数据样本有K类,生成学习算法是通过对原始数据类 p(x|Ck) 与 p(Ck) 建立数据类模型后,采用贝叶斯定理从而得出后验概率 p(Ck|x) 。对待分类样本x分别计算属于每个类别的后验概率 p(Ck|x) ,取最大可能的类别。
二分类的情况:(K=2)
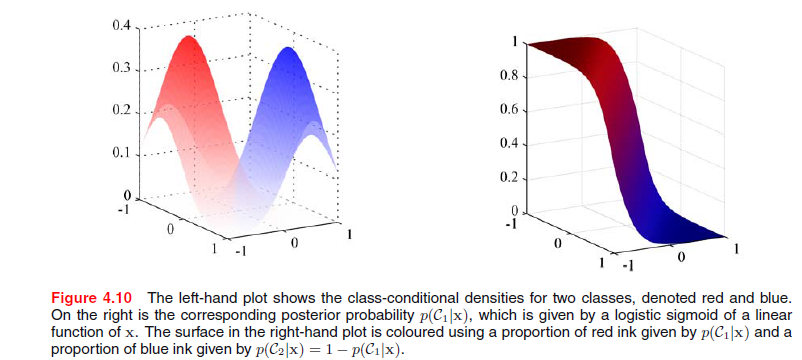
p(C1|x)=p(x,C1)p(x)=p(x|C1)p(C1)p(x|C1)p(C1)+p(x|C2)p(C2)=11+exp(−α)=σ(α)其中 α=lnp(x|C1)p(C1)p(x|C2)p(C2) ;函数 σ(α)=11+exp(−α) 称为sigmoid函数。多类的情况:(K>2)
多分类的情况,是二分类的扩展,称为softmax函数。同样采用贝叶斯定理:p(Ck|x)=p(x|Ck)p(Ck)∑jp(x|Cj)p(Cj)=exp(αk)∑jexp(αj)
其中 αk=lnp(x|Ck)p(Ck) 。
1.2高斯分布假设
对于连续变量x,我们首先假设给定具体类条件下数据密度函数
p(x|Ck)
分布服从多维高斯分布,同时所有类别
p(x|Ck)
具有相同的协方差矩阵
∑
:
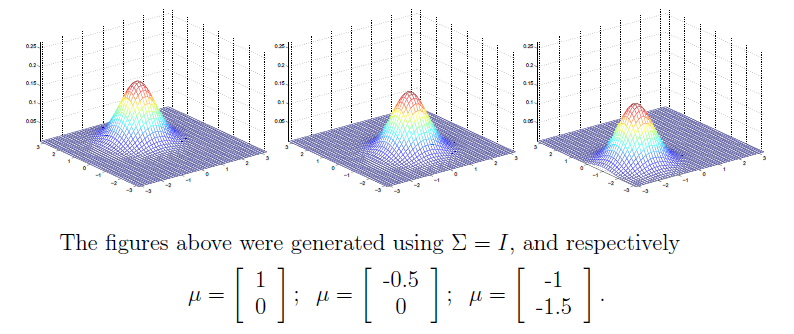
二维高斯分布,相同方差,不同期望的三个图形。
- 二分类情况K=2
把多维高斯分布公式带入上述对应的贝叶斯公式得:
注意到sigmoid函数参数是关于数据x的线性函数
下图是2维数据的高斯分布图形:
- 多分类的情况K>2
多维高斯分布函数带入softmax函数得:
注意: αk(x) 也是关于样本数据x的线性函数
实际上,无论是连续型数据还是下面将要介绍的离散型数据(朴素贝叶斯分类),只要假设的分布属于指数簇函数,都有广义线性模型的结论。
K=2时为sigmoid函数:参数 λ 为模型的固有参数
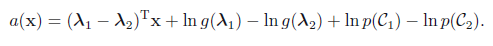
K>2时为softmax函数:
1.3模型参数的求解
在假设了数据类密度函数
p(x|Ck)
的情况下,下面需要对模型的参数进行求解。例如,上述假设了数据为高斯分布,需要计算先验概率
p(Ck)
及参数
μk,∑
.我们采用最大化释然函数的方法求解:
考虑二分类的情况:样本数据为
(xn,tn)
,样本总量为N,
tn=1
属于
C1
类,总数为
N1
;
tn=0
属于
C2
类,总数为
N2
.假设先验概率
p(C1)=π
;则
p(C2)=1−π
释然函数: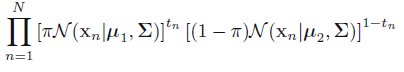
分别求偏导数并令为0,得:
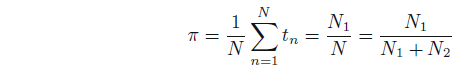

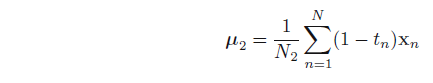
2.朴素贝叶斯分类器(NBC)
2.1概念
朴素贝叶斯分类器是生成学习算法的一种。考虑一个样本
x=(x1,x2,x3...xD)
,有D个特征,每个特征
xi
取值为有限的离散值,这时需要对
p(x|y)
建立模型。朴素贝叶斯算法做了一种很强的假设:即给定类别y=c的情况下,每种特征之间相互独立,即有
p(x1|y,x2)=p(x1|y)
;
p(x1,x2|y)=p(x1|y)p(x2|y)
所以有:
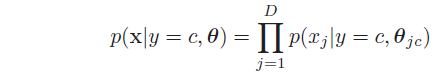
条件类概率
p(x|y)
可根据数据类型建立不同的形式:
- 当样本数据x取实数值为时,采用高斯分布: p(x|y=c,θ)=∏Dj=1N(xj|μjc,σ2jc)
- 当每种特征 xj∈{0,1} 时,采用伯努利分布 p(x|y=c,θ)=∏Dj=1Ber(xj|μjc)
- 当每种特征取值 xj∈{1,2,3,...,K} ,可以采用multinoulli distribution: p(x|y=c,θ)=∏Dj=1Cat(xj|μjc)
2.2文本分类
朴素贝叶斯虽然做了很强的特征独立性假设,却对在文本分类的情况效果很好。
首先收集所有样本数据中出现过的词,建立一个有序字典,长度为D。对待分类文本x依据字典建立一个长度为D词向量,
x=(x1,x2,x3,....,xD)
,每种特征
xj∈{0,1}
。即
xj=1
表示字典中第j个词在此文本中出现过;反之,
xj=0
表示字典中第j个词没有在文本中出现过,采用伯努利分布
p(x,y)=p(y)p(x|y)=p(y)∏Dj=1Ber(xj|μjc)
。
定义:
ϕi|y=0=p(xi=1|yi=0)
,
ϕi|y=1=p(xi=1|yi=1)
,
ϕy=p(y=1)
释然函数:
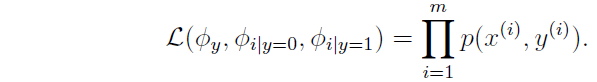
最大释然估计得:
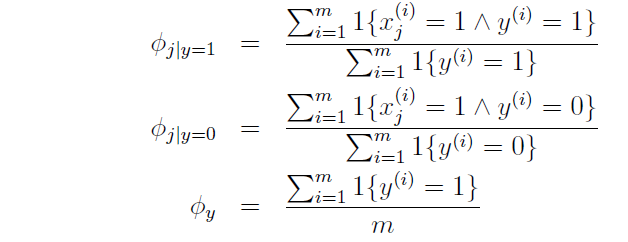
训练出模型后,对待分类样本根据贝叶斯定理,计算每种类别的后验概率,选择最大的后验概率类别:
2.3拉普拉斯平滑
在对文本分类的情况下,假如我们训练分类器采用的训练文本所有
xj
都为0时,这时模型参数
ϕj|y=0=0
,
ϕj|y=1=0
,这时如果需要对待一个文本x分类且
xj=1
,根据上述朴素贝叶斯方法,得到每种后验概率都为0,即
p(y=1|x)=0,P(y=0|x)=0
。这是由于上述乘法的缘故,根本原因是
ϕj|y=0=0
,
ϕj|y=1=0
。由于样本量有限,预测某个事件的发生概率为0,也是不准确的。
为了解决这种情况,可以模型参数的分子加上1,同时保持和为1,,称为拉普拉斯平滑。
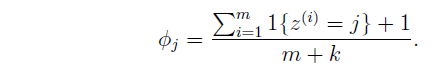
参考:PRML&&MLAPP










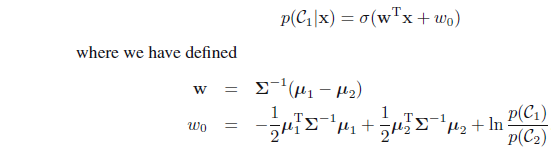
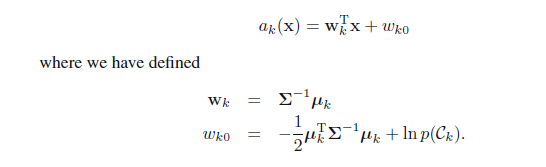
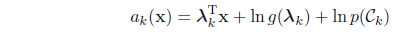
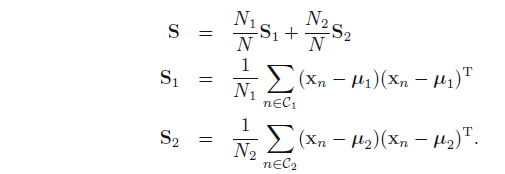
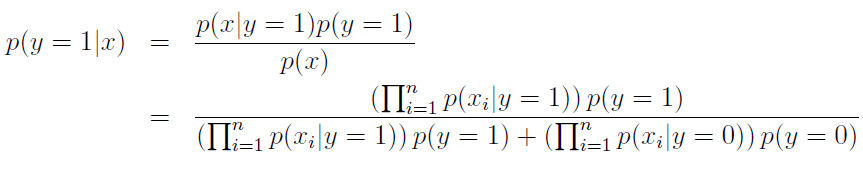
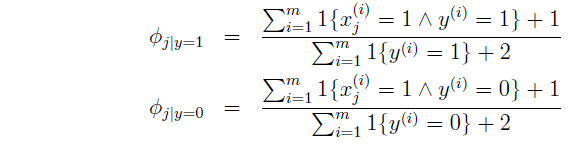














 272
272

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








