序列最小最优化算法（SMO算法）

最新推荐文章于 2022-04-10 17:01:32 发布

是帆帆不是凡凡呀

最新推荐文章于 2022-04-10 17:01:32 发布

阅读量3.7k

点赞数 12

分类专栏：笔记文章标签：算法支持向量机机器学习

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/m0_61624005/article/details/122218831

版权

前面三篇我已经谈了谈我对支持向量机的理解，推到了各类支持向量机的对偶算法，我们有很多最优化算法来求解这个问题，但是样本容量很大时，这些算法会变得非常低效。人们就提出了很多快速实现算法，SMO算法就是其中之一，主要是用来解这个对偶问题：

$_{\alpha }^{min}\textrm{}\: \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha _{i}\alpha _{j}y_{i}y_{j}\left ( \phi \left ( x_{i} \right )\cdot\phi \left ( x_{j} \right ) \right )-\sum_{i=1}^{N} \alpha _{i}$

s.t. $\sum_{i=1}^{N}\alpha _{i}y_{i}= 0$

$0\leq \alpha _{i}\leq C,i=1,2,\cdots ,N$

这个问题中变量是拉格朗日乘子，一个变量对应一个样本点，变量的总数即为样本容量N，也就是说我们现在要求的这个函数是N元函数。

在介绍SMO之前，大家可以先了解下坐标上升算法，这两个算法类似。

坐标上升算法

坐标上升算法每次更新多元函数中的一维，经过多次迭代直到收敛达到优化函数的目的。

下图中从A点到F*红色线所示就是这个过程。

这里写图片描述

SMO算法

上面已经提到了我们需要优化N个变量，SMO算法就是将N个参数的二次规划问题分成了多个二次规划问题，每个子问题只需要求解两个参数。

为什么要两个两个求？

我们要选择一对变量，因为在SVM中变量是相互关联的： $\sum_{i=1}^{N}\alpha _{i}y_{i}= 0$ ，若只固定一个 $\alpha _{1}$ ，当我们对 $\alpha _{1}$ 修正后，等号将不再成立。我们至少需要两个来保证等式成立。

我们先选取两个需要优化的参数为 $\alpha _{1}$ ， $\alpha _{2}$ （参数的选取不是随意的，在最后会介绍）,其他变量是固定的，

将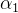 $\alpha _{1}$ ， $\alpha _{2}$ 带入上述对偶问题式子：

最低0.47元/天解锁文章

是帆帆不是凡凡呀

关注

12
点赞
踩
52

收藏

觉得还不错? 一键收藏
6
评论
序列最小最优化算法（SMO算法）

前面三篇我已经谈了谈我对支持向量机的理解，推到了各类支持向量机的对偶算法，这一篇的SMO算法主要是用来解这个对偶问题：
复制链接

扫一扫

专栏目录

评论 6

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。