图

如果图中任意两点都是连通的，那么图被称作连通图。如果此图是有向图，则称为强连通图

１，图（Ｇｒａｐｈ）是由顶点的有穷非空集合和顶点之间的边的集合组成，通常表示为：Ｇ（Ｖ，Ｅ），

　　其中，Ｇ表示一个图，Ｖ是图Ｇ中顶点的集合，Ｅ是图Ｇ中边的集合

　　１，线性表中我们把数据元素叫元素，树中将数据元素叫节点，在图中数据元素，

              我们则称之为顶点（Ｖｅｒｔｅｘ）

　　２，线性表中可以没有数据元素，称为空表．数中可以没有节点，叫做空树．但是对于图而言，

　　　　不允许没有顶点，顶点集合是有穷非空的

　　３，线性表中，相邻的数据元素之间具有线性关系，树结构中，相邻的两层节点具有层次关系．

　　　　而图中，任意两定点之间都可能有关系．

２，无向边：若顶点Vi到Vj之间的边没有方向，则称这条边为无向边（Ｅｄｇｅ），用无序偶对

      （Vi，Vj）来表示。如果图中任意两个顶点之间的边都是无向边，则称该图为无向图

　　

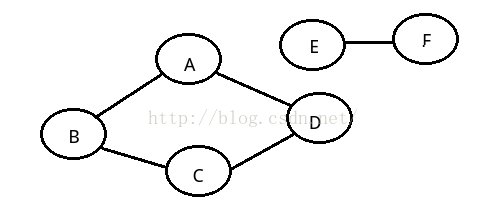
　　如上：无向图G1来说：G1= {V1,{E1}}，其中顶点集合V1={A,B,C,D};边集合

       E1 = {(A,B),(B,C),(C,D),(D,A),(A,C)};

　　有向边：若从顶点Vi到Vj的边为有方向，则称这条边为有向边，也称为弧（Ａｒｃ），用有序偶

       <Vi,Vj>来表示，Vi称为弧尾（Ｔａｉｌ），Vj称为弧头（Ｈｅａｄ）。如果图中任意两个顶点之间

　　的边都是有向边，则称该图为有向图。如下：

　　

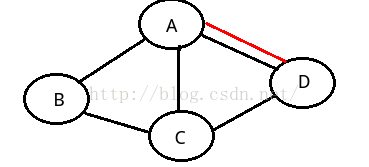
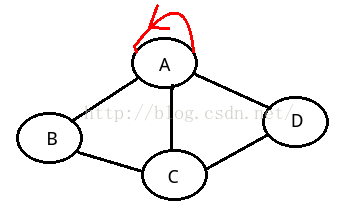
       简单图：在图中，若不存在顶点到其自身的边，且同一条边不重复出现。

　　　　　　

　　　　　　如上两个图都不是简单图。。。

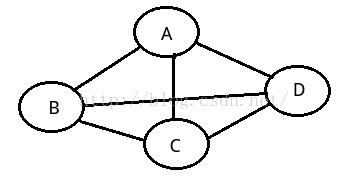
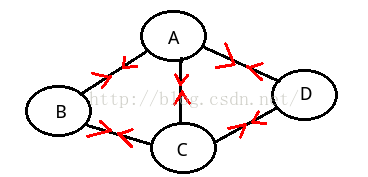
　　无向完全图：在无向图中，如果任意两个顶点之间都存在边。如下图....。。。。

　　　　　　　　

　　有向完全图：如果任意两个顶点之间都存在方向互为相反的两条弧。

　　　　　　　　

　　稀疏图：有很少条边的图

　　稠密图：有很多条边的图（相对而言。。。）

　　网：图的边或者弧有与它相关的数字，这种与图的边或弧相关的数叫做权（ｗｅｉｇｈｔ）。权可以表示

　　　　从一个顶点到与另一个顶点的距离或耗费。。。称之为往。。。

　　连通图：任意两个顶点都是连通的。。。。

　　　　　　

　　　　　　如上图：Ａ永远都到不了Ｅ，所以不是连通图。。。

　　无向图节点的边数叫做度，有向图的顶点分为入度和出度

１，邻接矩阵

　　图的邻接矩阵存储方式是用两个数组来表示图。

　　一个一维数组存储图中的顶点信息，一个二维数组存储图中的边或弧的信息　　　

　　

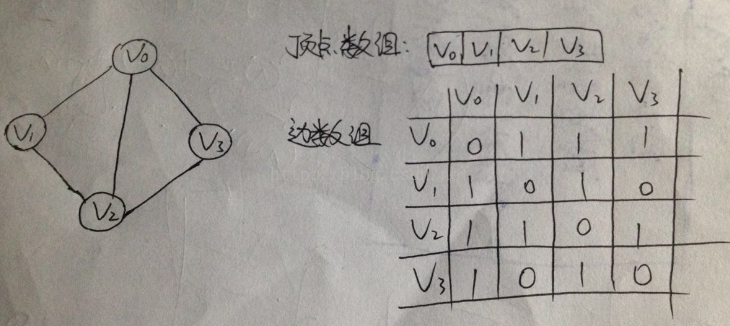
　　（无向图）

　　

　　可以知道：无向图是一个对称矩阵。。。。。　　　　　　　　　

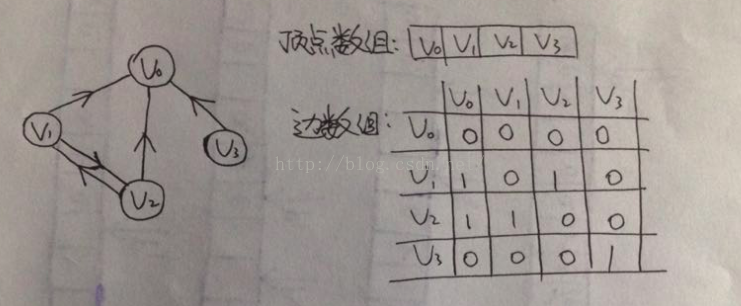
　　（有向图）

　　

　　有向图讲究出度和入度，我们正好可以根据行列各数之和求出入度和出度。。。。。

　　

　　（网）

　　　

　　

　　我们用无穷来表示一个计算机允许的，大于所有边上权值的值，也就是一个不可能的极限值。。。。

　　为什么不用０来表示呢？？？

　　权值大多数情况下是正值，但是个别时候可能就算０，甚至有可能是负值（范围表示）　　　　

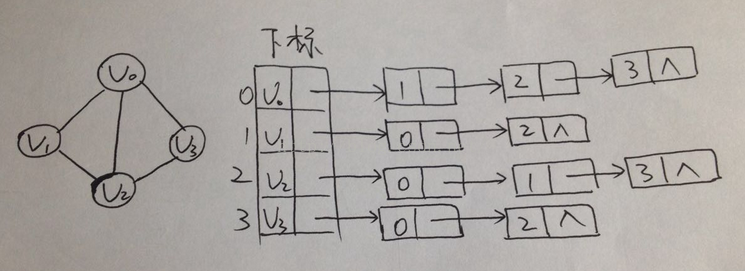
２，邻接表

　　邻接矩阵是不错的一种图存储结构，但是我们也发现，对于边数相对较少的图，这种结构是

　　对存储空间的极大的浪费。如：我们的图为下面的稀疏图的时候。

　　

　　所以，我们就需要考虑另外一种存储结构了，我们也知道：当顺序存储结构造成空间的浪费

　　问题的时候，出现了链式结构。所以：我们将数组和链表相结合产生的存储方式称为邻接表。

　　１，图中顶点用一个一维数组存储，此外：对于顶点数组中，每个数据元素还需要存储指向

　　　　第一个邻接点的指针。

　　２，图中每个顶点的所有邻接点构成一个线性表，由于邻接点的个数不一定，所以用单链表

　　　　存储。。。

　　（无向图）

　　

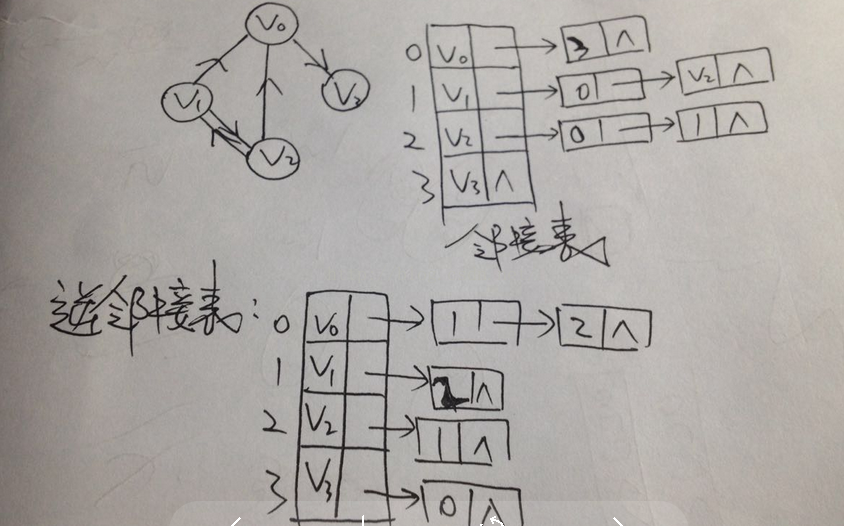
　　（有向图）　　　

　　

　　网：

　　　　

　　

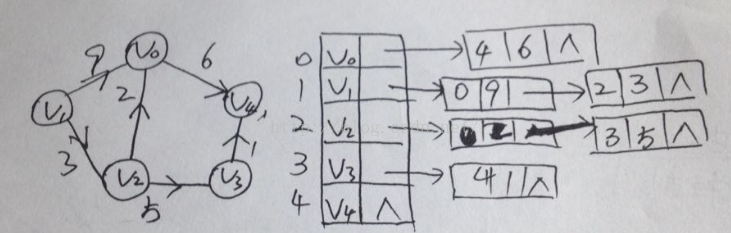
３，十字链表

　　对于有向图而言，邻接表是有缺陷的。关心了出度问题，想要知道入度就必须要遍历整个图才能直到，

　　反之，逆邻接表解决了入度却不了解出度的问题。那么有没有可以把邻接表和逆邻接表结合起来的方

　　法呢？？？

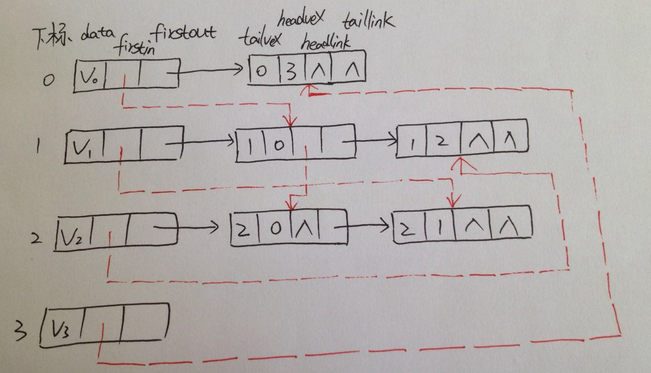
　　答案是肯定的，就是把它们整合在一起。这就是我们要提到的有向图的一种存储方式：十字链表

　　

　　　重新定义顶点表节点结构

　　

　　　其中firstin表示入边表头指针，指向该顶点的入边表中的第一个节点，firstout表示出边表头指针，

　　　指向该顶点的出边表中的第一个节点。

　　　　　　　　　　　　　　

　　　重新定义的边表节点结构　　　　

　　　　　　　　　

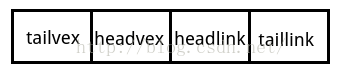
　　　其中tailvex是指弧起点在顶点表的下标，headvex是指弧终点在顶点表中下标，headlink是指入边表

　　　指针域，指向终点相同的下一条边，taillink是指边表指针域，指向起点相同的下一条边。如果是网

　　　，还可以增加一个weight域来存储权值。。。。。

　　　

          

　　　十字链表的好处就是将邻接表和逆邻接表整合在了一起，这样可以很容易的求出入度和出度。。。。

　　　同样的，除了结构复杂一点外，其实创建图算法的时间复杂度和邻接表是相同的。。。。

４，图的遍历

　　从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次。

　　１，深度优先

　　　　深度优先遍历（Depth_First_Search），也有称为深度优先搜索，简称ＤＦＳ。　　　

　　　　

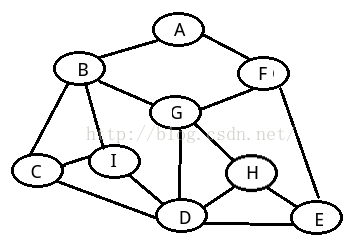
　　　我们深度遍历：Ａ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆ，Ｇ，Ｈ，Ｉ　

　　

　　２，广度优先遍历

　　　　广度优先遍历（Breadth_First_Search），又称为广度；优先搜索，简称ＢＦＳ

　　　　

　　　　同样的，我们广度搜索：Ａ，（Ｂ，Ｆ），（Ｃ，Ｉ，Ｇ，Ｅ），（Ｄ，Ｈ）

５，最小生成树　

　　我们把构造连通网的最小代价生成树称为最小生成树（Ｍinimum Cost Spanning Tree）

      

　　１，尽可能选取权值小的边，但是不能构成回路

　　２，选取ｎ－１条恰当的边以连接网中的ｎ个顶点

       找连通网的最小生成树，经典的有两种算法：普利姆算法和科鲁斯卡尔算法（都属于贪心算法）

　　１，普利姆（Ｐｒｉｍ）算法　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　1).输入：一个加权连通图，其中顶点集合为V，边集合为E；

　　2).初始化：V_new = {x}，其中x为集合V中的任一节点（起始点）

　　3).重复下列操作，直到V_new = V：

　　　a.在集合E中选取权值最小的边<u, v>，其中u为集合V_new中的元素，而v不在V_new集合当中，并且　　　　　　v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

　　　b.将v加入集合V_new中，将<u, v>边加入集合E_new中；

　　4).输出：使用集合V_new和E_new来描述所得到的最小生成树。

下面对算法的图例描述

图例	说明	不可选	可选	已选（Vnew）
	此为原始的加权连通图。每条边一侧的数字代表其权值。	-	-	-
	顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。	C, G	A, B, E, F	D
	下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。	C, G	B, E, F	A, D
	算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。	C	B, E, G	A, D, F
	在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。	无	C, E, G	A, D, F, B
	这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。	无	C, G	A, D, F, B, E
	顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。	无	G	A, D, F, B, E, C
	现在，所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。	无	无	A, D, F, B, E, C, G

　　

Kruskal算法

 

1.概览

Kruskal算法是一种用来寻找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪婪算法的应用。和Boruvka算法不同的地方是，Kruskal算法在图中存在相同权值的边时也有效。

 

2.算法简单描述

1).记Graph中有v个顶点，e个边

2).新建图Graph_new，Graph_new中拥有原图中相同的e个顶点，但没有边

3).将原图Graph中所有e个边按权值从小到大排序

4).循环：从权值最小的边开始遍历每条边 直至图Graph中所有的节点都在同一个连通分量中

                if 这条边连接的两个节点于图Graph_new中不在同一个连通分量中

                                         添加这条边到图Graph_new中

 

图例描述：

首先第一步，我们有一张图Graph，有若干点和边 

 

将所有的边的长度排序，用排序的结果作为我们选择边的依据。这里再次体现了贪心算法的思想。资源排序，对局部最优的资源进行选择，排序完成后，我们率先选择了边AD。这样我们的图就变成了右图

 

 

 

在剩下的变中寻找。我们找到了CE。这里边的权重也是5

依次类推我们找到了6,7,7，即DF，AB，BE。

下面继续选择， BC或者EF尽管现在长度为8的边是最小的未选择的边。但是现在他们已经连通了（对于BC可以通过CE,EB来连接，类似的EF可以通过EB,BA,AD,DF来接连）。所以不需要选择他们。类似的BD也已经连通了（这里上图的连通线用红色表示了）。

最后就剩下EG和FG了。当然我们选择了EG。最后成功的图就是右：

 

 

 

3.简单证明Kruskal算法

对图的顶点数n做归纳，证明Kruskal算法对任意n阶图适用。

归纳基础：

n=1，显然能够找到最小生成树。

归纳过程：

假设Kruskal算法对n≤k阶图适用，那么，在k+1阶图G中，我们把最短边的两个端点a和b做一个合并操作，即把u与v合为一个点v'，把原来接在u和v的边都接到v'上去，这样就能够得到一个k阶图G'(u,v的合并是k+1少一条边)，G'最小生成树T'可以用Kruskal算法得到。

我们证明T'+{<u,v>}是G的最小生成树。

用反证法，如果T'+{<u,v>}不是最小生成树，最小生成树是T，即W(T)<W(T'+{<u,v>})。显然T应该包含<u,v>，否则，可以用<u,v>加入到T中，形成一个环，删除环上原有的任意一条边，形成一棵更小权值的生成树。而T-{<u,v>}，是G'的生成树。所以W(T-{<u,v>})<=W(T')，也就是W(T)<=W(T')+W(<u,v>)=W(T'+{<u,v>})，产生了矛盾。于是假设不成立，T'+{<u,v>}是G的最小生成树，Kruskal算法对k+1阶图也适用。

由数学归纳法，Kruskal算法得证。

７，最短路径。。。。。

　　最短路径是指两顶点之间经过的边上的权值之和最少的路径，并且我们称为路径上的第一个顶点是源点

　　，最后一个是终点。。。。

       

Dijkstra算法

1.定义概览

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。注意该算法要求图中不存在负权边。

问题描述：在无向图 G=(V,E) 中，假设每条边 E[i] 的长度为 w[i]，找到由顶点 V0 到其余各点的最短路径。（单源最短路径）

 

2.算法描述

1)算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

2)算法步骤：

a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。

b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

d.重复步骤b和c直到所有顶点都包含在S中。

 

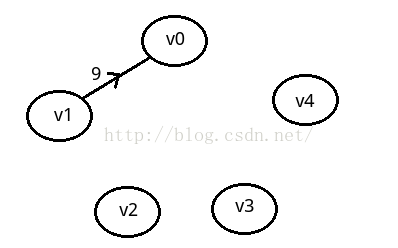
执行动画过程如下图

 

先给出一个无向图

用Dijkstra算法找出以A为起点的单源最短路径步骤如下

一.问题引入

        问题：从某顶点出发，沿图的边到达另一顶点所经过的路径中，各边上权值之和最小的一条路径——最短路径。解决最短路的问题有以下算法，Dijkstra算法，Bellman-Ford算法，Floyd算法和SPFA算法，另外还有著名的启发式搜索算法A*，不过A*准备单独出一篇，其中Floyd算法可以求解任意两点间的最短路径的长度。笔者认为任意一个最短路算法都是基于这样一个事实：从任意节点A到任意节点B的最短路径不外乎2种可能，1是直接从A到B，2是从A经过若干个节点到B。

二.Dijkstra算法

        该算法在《数据结构》课本里是以贪心的形式讲解的，不过在《运筹学》教材里被编排在动态规划章节，建议读者两篇都看看。

          

        观察右边表格发现除最后一个节点外其他均已经求出最短路径。

        (1)   迪杰斯特拉(Dijkstra)算法按路径长度(看下面表格的最后一行，就是next点)递增次序产生最短路径。先把V分成两组：

• S：已求出最短路径的顶点的集合
• V-S=T：尚未确定最短路径的顶点集合

        将T中顶点按最短路径递增的次序加入到S中，依据：可以证明V0到T中顶点Vk的最短路径，或是从V0到Vk的直接路径的权值或是从V0经S中顶点到Vk的路径权值之和（反证法可证，说实话，真不明白哦）。

        (2)   求最短路径步骤

1. 初使时令 S={V0},T={其余顶点}，T中顶点对应的距离值， 若存在<V0,Vi>，为<V0,Vi>弧上的权值（和ＳＰＦＡ初始化方式不同），若不存在<V0,Vi>，为Inf。
2. 从T中选取一个其距离值为最小的顶点W(贪心体现在此处)，加入S(注意不是直接从S集合中选取，理解这个对于理解vis数组的作用至关重要)，对T中顶点的距离值进行修改：若加进W作中间顶点，从V0到Vi的距离值比不加W的路径要短，则修改此距离值（上面两个并列for循环，使用最小点更新）。
3. 重复上述步骤，直到S中包含所有顶点，即S=V为止（说明最外层是除起点外的遍历）。

        下面是上图的求解过程，按列来看，第一列是初始化过程，最后一行是每次求得的next点。

          

        (3)   问题：Dijkstar能否处理负权边？（来自《图论》）

             答案是不能，这与贪心选择性质有关(ps：貌似还是动态规划啊，晕了)，每次都找一个距源点最近的点（dmin），然后将该距离定为这个点到源点的最短路径；但如果存在负权边，那就有可能先通过并不是距源点最近的一个次优点（dmin'），再通过这个负权边L(L<0)，使得路径之和更小（dmin'+L<dmin）,则dmin'+L成为最短路径，并不是dmin，这样dijkstra就被囧掉了。比如n=3，邻接矩阵：
0，3，4
3，0，-2
4，-2，0,用dijkstra求得d[1，2]=3，事实上d[1，2]=2，就是通过了1-3-2使得路径减小。不知道讲得清楚不清楚。

二.Floyd算法

        参考了南阳理工牛帅(目前在新浪)的博客。

        Floyd算法的基本思想如下：从任意节点A到任意节点B的最短路径不外乎2种可能，1是直接从A到B，2是从A经过若干个节点到B，所以，我们假设dist(AB)为节点A到节点B的最短路径的距离，对于每一个节点K，我们检查dist(AK) + dist(KB) < dist(AB)是否成立，如果成立，证明从A到K再到B的路径比A直接到B的路径短，我们便设置 dist(AB) = dist(AK) + dist(KB)，这样一来，当我们遍历完所有节点K，dist(AB)中记录的便是A到B的最短路径的距离。

        很简单吧，代码看起来可能像下面这样：

for (int i=0; i<n; ++i) {

  for (int j=0; j<n; ++j) {

    for (int k=0; k<n; ++k) {

      if (dist[i][k] + dist[k][j] < dist[i][j] ) {

        dist[i][j] = dist[i][k] + dist[k][j];

      }

    }

  }

}

        但是这里我们要注意循环的嵌套顺序，如果把检查所有节点K放在最内层，那么结果将是不正确的，为什么呢？因为这样便过早的把i到j的最短路径确定下来了，而当后面存在更短的路径时，已经不再会更新了。

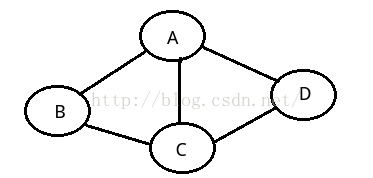
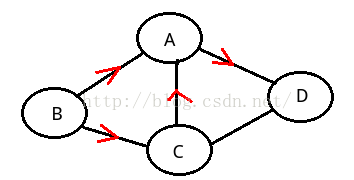
        让我们来看一个例子，看下图：

        图中红色的数字代表边的权重。如果我们在最内层检查所有节点K，那么对于A->B，我们只能发现一条路径，就是A->B，路径距离为9，而这显然是不正确的，真实的最短路径是A->D->C->B，路径距离为6。造成错误的原因就是我们把检查所有节点K放在最内层，造成过早的把A到B的最短路径确定下来了，当确定A->B的最短路径时dist(AC)尚未被计算。所以，我们需要改写循环顺序，如下：

        ps：个人觉得，这和银行家算法判断安全状态(每种资源去测试所有线程)，树状数组更新(更新所有相关项)一样的思想。

for (int k=0; k<n; ++k) {

  for (int i=0; i<n; ++i) {

    for (int j=0; j<n; ++j) {

            /*

            实际中为防止溢出，往往需要选判断 dist[i][k]和dist[k][j

            都不是Inf ，只要一个是Inf，那么就肯定不必更新。 

            */

      if (dist[i][k] + dist[k][j] < dist[i][j] ) {

        dist[i][j] = dist[i][k] + dist[k][j];

      }

    }

  }

}

        如果还是看不懂，那就用草稿纸模拟一遍，之后你就会豁然开朗。半个小时足矣（早知道的话会节省很多个半小时了。。）

       再来看路径保存问题：

void floyd() {

      for(int i=1; i<=n ; i++){

        for(int j=1; j<= n; j++){

          if(map[i][j]==Inf){

               path[i][j] = -1;//表示  i -> j 不通 

          }else{

               path[i][j] = i;// 表示 i -> j 前驱为 i

          }

        }

      }

      for(int k=1; k<=n; k++) {

        for(int i=1; i<=n; i++) {

          for(int j=1; j<=n; j++) {

            if(!(dist[i][k]==Inf||dist[k][j]==Inf)&&dist[i][j] > dist[i][k] + dist[k][j]) {

              dist[i][j] = dist[i][k] + dist[k][j];

              path[i][k] = i;

              path[i][j] = path[k][j];

            }

          }

        }

      }

    }

    void printPath(int from, int to) {

        /*

         * 这是倒序输出，若想正序可放入栈中，然后输出。

         * 

         * 这样的输出为什么正确呢？个人认为用到了最优子结构性质，

         * 即最短路径的子路径仍然是最短路径

         */

        while(path[from][to]!=from) {

            System.out.print(path[from][to] +"");

            to = path[from][to];

        }

    }