提要
重心座标插值在图形学领域有着很重要的应用,比如Ray Tracing算法的ray - triangle intersection 检测,比如有限元模拟中的模型简化等。
一维情况
从最简单的开始,一个线段:
如何表示p点的值?
可以这样想,p总是在x1和x2之间徘徊,不知道如何选择,蓝色线段的长度t表示p对x2的喜爱程度,红色线段(1-t)表示对x1的喜爱程度。
那么P点的值就可以表示为
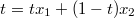
二维情况
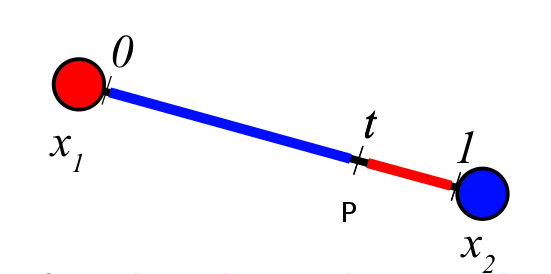
二维情况下就是三角形了。
求点p的值。
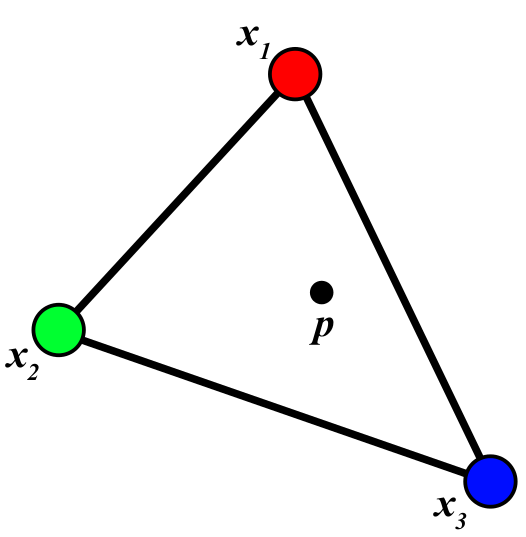
二维情况下就应该联想到面积。想法类似,如下图:
蓝色三角形面积A3表示p喜爱蓝色点的程度,绿色三角形和红色三角形同理。
那么p点的座标就可以表示为:
令 u = A1/A ,v = A2/A, w = A3/A
则式子可以化为
ux1 + vx2 + wx3.
其中 u+v+w=1.
求三角形面积
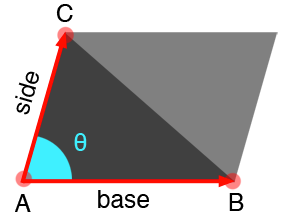
已知三角形三个顶点的座标值,求三角形面积。如下图
首先求平行四边形的面试,用到的是向量的点乘。
Parallelogramarea= ||(B−A)×(C−A)||Trianglearea=Parallelogramarea2Parallelogramarea= ||(B−A)×(C−A)||Trianglearea=Parallelogramarea2Parallelogramarea= ||(B−A)×(C−A)||Trianglearea=Parallelogramarea2Parallelogramarea= ||(B−A)×(C−A)||Trianglearea=Parallelogramarea2Parallelogramarea= ||(B−A)×(C−A)||
三角形面积除以2就可以了。
Trianglearea=||(B−A)||∗||(C−A)||sin(θ)2
三维情况
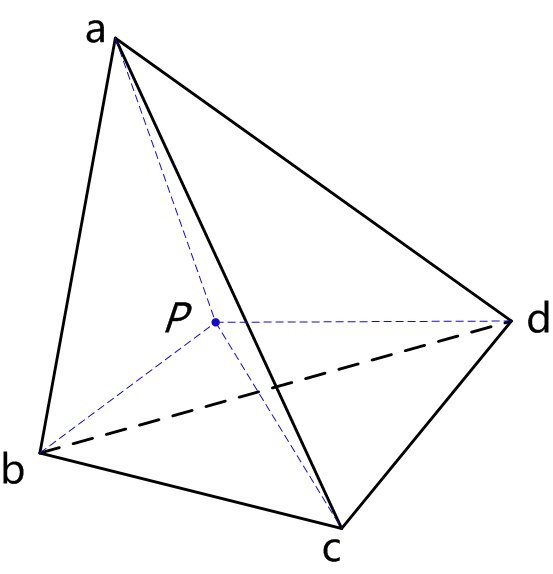
三维1情况对应的就是四面体( Tetrahedron)了。如下图,还是求P点的值。
也许大家第一想到的是体积是这样的,计算每个小四面体的体积,然后和最大的四面体体积相比,得到对应的比例,原理是这样的,但是有更加简单的方法!
首先定义点到平面的有向距离为:D(p , PLabc),其中p、a、b、c均为空间上的点,而PL是由a、b、c三个点所构成的平面,那么对于上图分布的一个四面体以及另外的任意一个点P,可得该点的重心坐标为:

其中的![]() ,
,![]() ,
,![]() ,
,![]() 分别是P点相对于a,b,c,d点的权重,而且有
分别是P点相对于a,b,c,d点的权重,而且有![]() +
+![]() +
+![]() +
+![]() = 1
= 1
有了重心坐标之后就可以使用其来判断P点与该四面体间的关系:
- 如果
 ,
, ,
, ,
, 均属于[0,1],那么P点位于该四面体的内部。
均属于[0,1],那么P点位于该四面体的内部。 - 如果其中某一项不在此范围内,还可以根据其越域方式来判断P点在四面体外的分布情况:比如
 小于0,那么P点就处于bcd所对应的平面之下(此处用a点来参考平面的上下);反之,若其大小1,那么P点就处于过P点且平行于bcd平面的平面之上。
小于0,那么P点就处于bcd所对应的平面之下(此处用a点来参考平面的上下);反之,若其大小1,那么P点就处于过P点且平行于bcd平面的平面之上。
参考
Barycentric Coordinates - http://www.scratchapixel.com/lessons/3d-basic-lessons/lesson-9-ray-triangle-intersection/barycentric-coordinates/
Barycentric Coordinates of Tetrahedron - http://blog.csdn.net/bugrunner/article/details/7423727





 本文深入探讨了重心坐标插值在图形学领域的应用,包括RayTracing算法、有限元模拟和几何形状操作。从一维线段到二维三角形再到三维四面体,详细介绍了如何通过面积和向量计算来实现点的插值。同时提供了求解三角形和四面体面积的方法,并解释了如何利用重心坐标判断点与几何体的位置关系。
本文深入探讨了重心坐标插值在图形学领域的应用,包括RayTracing算法、有限元模拟和几何形状操作。从一维线段到二维三角形再到三维四面体,详细介绍了如何通过面积和向量计算来实现点的插值。同时提供了求解三角形和四面体面积的方法,并解释了如何利用重心坐标判断点与几何体的位置关系。
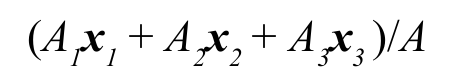
















 1801
1801

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








