算法的时间复杂度和空间复杂度

最新推荐文章于 2024-07-14 12:59:30 发布

泡泡茶壶Wending

最新推荐文章于 2024-07-14 12:59:30 发布

阅读量506

点赞数

分类专栏：算法

算法专栏收录该内容

6 篇文章 1 订阅

订阅专栏

时间复杂度

时间复杂度简单的理解就是执行语句的条数。如果有循环和递归，则忽略简单语句，直接算循环和递归的语句执行次数。

比如：

[java]view plaincopy 
   
 int x = 1;//时间复杂度为O(1)  
 for(int i=0; i<n; i++) {  
     System.out.println(i);  
 }//时间复杂度为O(n)  

具体例子：

1、O(1)

[java]view plaincopy 
   
 int x = 1;  

2、O(n)

[java]view plaincopy 
   
 for(int i=0; i<n; i++) {  
     System.out.println(i);  
 }  

3、O(

)

[html]view plaincopy 
   
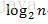 int n = 8, count = 0;;  
 for(int i=1; i<=n; i *= 2) {  
     count++;  
 }  

4、

[html]view plaincopy 
   
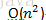
 int n = 8, count = 0;;  
 for(int i=1; i<=n; i++) {  
     for(int j=1; j<=n; j++) {  
         count++;  
     }  
 }  

5、

[java]view plaincopy 
   
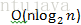
 int n = 8, count = 0;;  
 for(int i=1; i<=n; i *= 2) {  
     for(int j=1; j<=n; j++) {  
         count++;  
     }  
 }  

所举例子都比较简单。

空间复杂度

空间复杂度也很简单的理解为临时变量占用的存储空间。一个简单例子：

[java]view plaincopy 
   
 //交换两个变量x和y  
 int x=1, y=2;  
 int temp = x;  
 x = y;  
 y = temp;  

一个临时变量temp，所以空间复杂度为O(1)。

要在 hash 表中找到一个元素就是 O(1)
要在无序数组中找到一个元素就是 O(n)

访问数组的第 n 个元素是 O(1)
访问链表的第 n 个元素是 O(n)

我给你一个简单的判断方法:
如果实现中没有循环就是 O(1)
如果实现中有一个循环就是 O(n)

举个简单的例子，要从0加到n，我们会这么写：
int sum = 0;
for(int i = 0; i<=n; ++i)
{
   sum += i;
}
一共算了n次加法，那么就说这个时间复杂度是O(n)。当然O(n)的精确的概念是，是n的最高次方，比如，某个计算共计算了3n + 2次，那么这个时间复杂度也是O(n)，因为3n + 2中的最高次方是n。

如果代码这么写：
int sum = 0;
for(int i = 0; i<=n; ++i)
{
   for(int j = 0; j <=n; ++j)
   {
      sum += (i + j);
   }
}

很显然一共算了n^2次加法，那么就说这个时间复杂度是O(n^2)，和上面类似，如果某个算法计算了3*n^2 + n + 1次，其时间复杂度仍然是O(n^2)，因为3*n^2 + n + 1中最高的次方是n^2

所谓O(1)就是计算的次数是个常量，我们还以上面从0加到n的例子来说，如果我们用等差数列的公式，那么，代码可以这么写：
int sum = n * (n + 1) / 2
不管n有多大(当然不能溢出了)，通过上面的公式只需计算一次，也就说计算的次数是不变的，这种情况的时间复杂度就可以说成O(1)。再比如如果某个计算，不管其他条件怎么变化，均只需计算5次即可得出结果，那么这种情况的时间复杂度，也是O(1)。