本科课程参见:《软件学院那些课》
牛顿迭代公式
设已知方程f(x)=0的近似根x0 ,则在x0附近f(x)可用一阶泰勒多项式 近似代替.因此, 方程f(x)=0可近似地表示为p(x)=0。用x1表示p(x)=0的根,它与f(x)=0的根差异不大.
近似代替.因此, 方程f(x)=0可近似地表示为p(x)=0。用x1表示p(x)=0的根,它与f(x)=0的根差异不大.
设  ,由于x1满足
,由于x1满足 解得
解得

重复这一过程,得到迭代公式:

这就是著名的牛顿迭代公式,它相应的不动点方程为

Jacobi迭代公式解线性方程组
线性方程组基本解法:

若 方程组可同解变形为
方程组可同解变形为

Jacobi迭代法的计算公式:
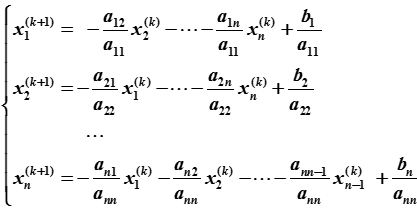
即 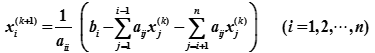
算法代码
/*简单迭代法的代码实现*/
#include<iostream>
#include<string>
#include<cmath>
using namespace std;
double e=2.718281818284;
double f(double x){
return pow(e,-1*x);
}
void SimpleDiedai(double x,double d){
double a=x;
double b=f(a);
int k=0;//记录循环的次数
while(((a-b)>d) || ((a-b)<-1*d)){
cout<<a<<endl;
a=b;
b=f(a);
k++;
if(k>100){
cout<<"迭代失败!(可能是函数不收敛)"<<endl;
return ;
}
}
cout<<b<<endl;
return;
}
int main(){
cout<<"请输入初始值x0和要求得结果的精度:";
double x,d;
cin>>x>>d;
SimpleDiedai (x,d);
return 0;
}
/*牛顿迭代法的代码实现*/
#include<iostream>
#include<string>
#include<cmath>
using namespace std;
double e=2.718281818284;
double f(double x){
double a=pow(e,-1*x);
return x-(x-a)/(1+a);
}
void NewtonDiedai(double x,double d){
double a=x;
double b=f(a);
int k=0; //记录循环的次数
while(((a-b)>d) || ((a-b)<-1*d)){
cout<<a<<endl;
a=b;
b=f(a);
k++;
if(k>100){
cout<<"迭代失败!(可能是函数不收敛)"<<endl;
return ;
}
}
cout<<b<<endl;
return;
}
int main(){
cout<<"请输入初始值x0和要求得结果的精度:";
double x,d;
cin>>x>>d;
NewtonDiedai(x,d);
return 0;
}
/*雅可比算法的代码实现*/
#include<iostream>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
//函数求数组中的最大值
double MaxOfList(vector<double>x){
double max=x[0];
int n=x.size();
for(int i=0;i<n;i++)
if(x[i]>max) max=x[i];
return max;
}
//雅可比迭代公式
void Jacobi(vector<vector<double> > A,vector<double> B,int n){
vector<double> X(n,0);
vector<double> Y(n,0);
vector<double> D(n,0);
int k=0; //记录循环次数
do{
X=Y;
for(int i=0;i<n;i++){
double tem=0;
for(int j=0;j<n;j++){
if(i!=j) tem += A[i][j]*X[j];
}
Y[i]=(B[i]-tem)/A[i][i];
cout<<left<<setw(8)<<Y[i]<<" ";
}
cout<<endl;
k++;
if(k>100){
cout<<"迭代失败!(可能是函数不收敛)"<<endl;
return ;
}
for(int a=0;a<n;a++){
D[a]=X[a]-Y[a];
}
}while( MaxOfList(D)>0.00001 || MaxOfList(D)<-0.00001);
return ;
}
int main(){
int n;
cout<<"请输入方程组未知数的个数n:";
cin>>n;
cout<<endl;
vector<vector<double> >A(n,vector<double>(n,0));
vector<double>B(n,0);
cout<<"请输入方程组的系数矩阵:"<<endl;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>A[i][j];
}
}
cout<<endl;
cout<<"请输入方程组的值向量:"<<endl;
for(int k=0;k<n;k++){
cin>>B[k];
}
cout<<endl;
cout<<"您输入的方程组为:"<<endl;
for(int a=0;a<n;a++){
for(int b=0;b<n;b++){
cout<<A[a][b]<<" ";
}
cout<<" "<<B[a]<<endl;
}
cout<<endl;
cout<<"由雅可比迭代公式求的方程组的解为:"<<endl;
Jacobi(A,B,n);
return 0;
}
实验过程原始记录
(1)分别用简单迭代法和牛顿迭代法求方程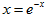 在x=0.5附近的一个根x*,要求精度为0.00001
在x=0.5附近的一个根x*,要求精度为0.00001
(输入0.5 0.000001)简单迭代法得到结果:
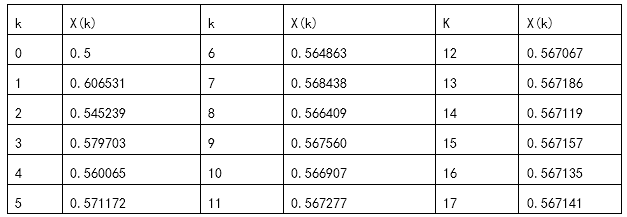
(输入0.5 0.000001)牛顿迭代法得到结果:
X0=0.5 x1=0.566311 x2=0.567143
(2)用雅可比迭代法求解方程组
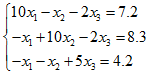
运行程序,根据提示输入 (3) (10 -1 -2 -1 10 -2 -1 -2 5) (7.2 8.3 4.2)
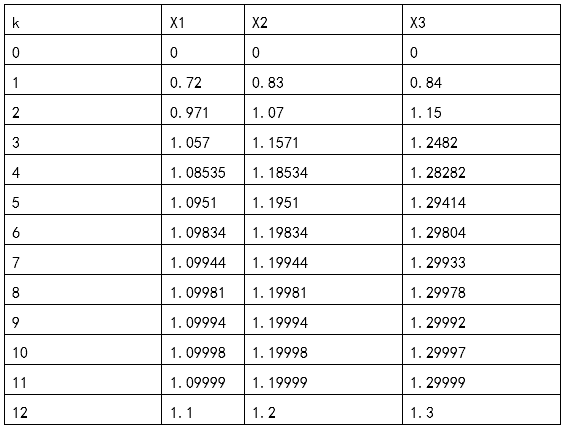
实验结果及分析
1、迭代法是一种逐次逼近法,这种方法使用某个固定公式-所谓迭代公式反复校正根的近似值,使之逐步精确化,直至满足精度要求的结果。迭代法是一种求解函数方程f(x)=0的解的方法,他解决了二分法无法求解复根级偶重根的问题,而其提高了收敛速度。迭代的思想是计算方法中基础的求解问题的思想。
2、简单迭代法的求根过程分成两步,第一步先提供根的某个猜测值,即所谓迭代初值,然后将迭代初值逐步加工成满足精度要求的根。迭代法的设计思想是:f (x) = 0等价变换成 然后由迭代公式 逐步球的满足精度的解。实际迭代中不同迭代函数的求解可能影响求的精确解的运算量,甚至可能因为函数发散而无法求解。解题时可通过对导函数的判断而判断函数是否发散,而编写代码时可以通过判断循环次数——即循环过多次而不能从循环中出来时就判断为死循环,无法求得正解
3、简单迭代法往往只是线性收敛,为得出超线性收敛的迭代格式,通常采用近似替代法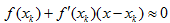 , 即牛顿公式
, 即牛顿公式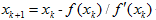 。迭代函数为 - / 牛顿法是一种逐步线性化方法。由实验结果可以看到,虽然选取近似公式,但牛顿迭代法仍能得到精度很高的解,而且牛顿迭代法大大提高了收敛速度。
。迭代函数为 - / 牛顿法是一种逐步线性化方法。由实验结果可以看到,虽然选取近似公式,但牛顿迭代法仍能得到精度很高的解,而且牛顿迭代法大大提高了收敛速度。
4、由迭代法求解线性方程组的基本思想是将联立方程组的求解归结为重复计算一组彼此独立的线性表达式,这就使问题得到了简化,类似简单迭代法转换方程组中每个方程式可得到雅可比迭代式
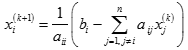
迭代法求解方程组有一定的局限性,例如要求方程组的系数矩阵具有某种特殊性质,以保证迭代过程的收敛性,但迭代法同时有十分明显的优点——算法简单,因而编制程序比较容易,所以在实际求解问题中仍有非常大利用价值。
(转载请注明作者和出处:http://blog.csdn.net/xiaowei_cqu 未经允许请勿用于商业用途)






 本文介绍了牛顿迭代法和Jacobi迭代法在解方程和线性方程组中的应用。通过算法代码展示迭代过程,并通过实验记录分析了两种方法的收敛速度和精度,指出牛顿法的高效性以及迭代法在解决线性方程组时的简化策略和局限性。
本文介绍了牛顿迭代法和Jacobi迭代法在解方程和线性方程组中的应用。通过算法代码展示迭代过程,并通过实验记录分析了两种方法的收敛速度和精度,指出牛顿法的高效性以及迭代法在解决线性方程组时的简化策略和局限性。
















 900
900

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








