最近刚接触A*寻路算法,听说是一种比较高效的自动寻路的算法,当然,事实也正是如此,这么好的东西,自然是要收入囊中的,说不定什么时候也能派上用场呢。为了学习这个,也是上网找了好多资料,看了好多博客,但是貌似有些关键点没有具体说明,所以自己也是费了不小的劲才完全理解。为了更好的讲解,特意花了一个晚上作了一系列说明图(作图真心不容易啊,如果发现图片有标注错的地方,大家多多包涵呀),希望大家能够有所收获。
启发式搜索
A*寻路算法是一种用来高效的寻路算法,那究竟是如何寻找最佳路径的呢?请看图:
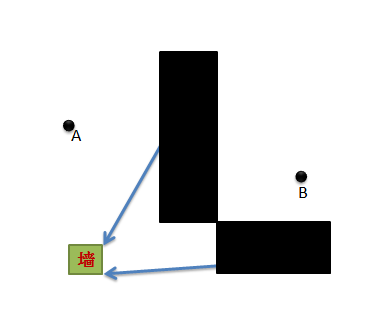
如图所示,图上有A、B两点,中间被墙隔开,我们如何找到一条最短的路径(或者最接近现实的路径),从A走到B呢?
图上除了A、B两点以及黑黑的墙以外,什么都没有,且别说计算最佳路径了,就连A、B两点的位置我们都无法准确表达出来,我们总该想想,通过什么方式来表达我们的路径,然后才能讨论最短路径的问题。所以我们必须借助工具才行,这工具就是“方格”。也就是说我们可以把这个小地图分割成一个个的小方格,这样便于我们表示A和B的位置,便于表示路径(当然,你可以分其他形状,It’s up to you!只要能达到目标即可),如下图所示:
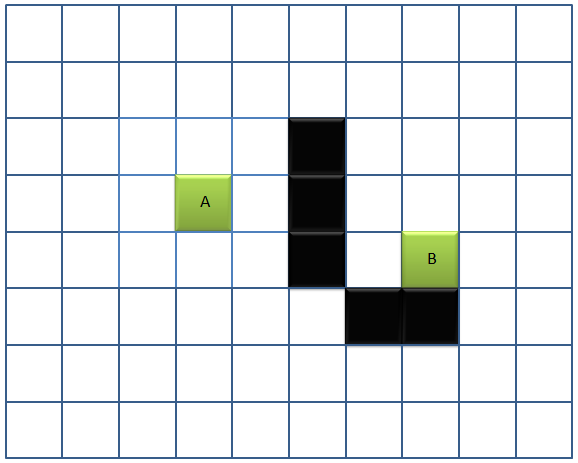
现在我们已经很清楚A、B的相对位置了,那接下来我们该怎么办呢?貌似直接找到一条最短的路径比较困难,我们是不是可以这样:我们从A点出发,先找A点邻近的方格,然后判断这个方格是否是最好的位置(离A点比较近,同时离B点也比较近),然后再从这个所谓的“最好的位置”扩展其邻近的方格,再找到一个“最好的位置”,一步一步逼近目标……显然,这是可行的,而我们也正是采用了这种方法。这也就是所谓的启发式搜索(启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径,提高了效率)。
路径评分
现在的问题是,如何判断这是不是“最好的位置”呢?这里涉及到一个估价函数的概念,顾名思义,就是一个评估费用的函数嘛,假如每走一个格子都要花费一定的钱,那你是不是要好好估算一下怎么样花钱最少,走哪条路到B点最省钱(我相信,为了省钱,你一定不会算错吧)。而在寻路问题中,我们通常使用”F=G+H“这样的估价函数对路径进行评估。
G:代表当前节点到起始点的距离(此处为到A点的距离)。
H:代表当前节点到终点的距离(此处为到B点的距离)。
F:则是两者之和。
也就是说,判断一个位置是否是“最好的位置”,就是判断其F值是否最小。这么说可能有些抽象,不太好理解,那我们来看具体的例子。
算法描述
首先,我们将起始点(A点)添加进一个叫“开启列表”的集合中(“开启列表”中的节点(方格)都在等待检查是否是“最好的位置”),然后我们检查开启列表中找到F值最低的节点,将其从“开启列表”中移除,再将其添加进一个叫“关闭列表”的集合中(“关闭列表”中存放着所有我们之前检查过的“最好的位置”,所以不需要再次检查),此时只有A点一个节点,所以我们将A点添加进关闭列表,并将A点置为“当前节点”,用来标识这是我们当前搜索到的最好的位置。我们需要通过当前节点来搜索当前节点邻近的节点(八个方向上的节点:上、下、左、右、左上、右上、左下、右下),因为这些点都有可能是A点下一步所走的节点,将它们添加进开启列表中,如图所示:
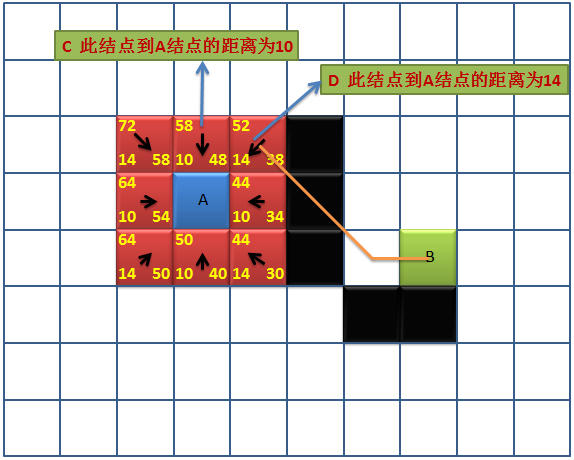
大家可以看到,A点被标识成蓝色,邻近的节点被标识为棕色,且上面都包含数字和箭头。
左下角的数字代表G值:与A节点水平或者垂直的节点到A的距离为10个单位长度(如图C节点),在A节点的斜对角线上的节点到A的距离为14个单位长度(如图D节点)。
右下角的数字代表H值: H值的计算方法可参考图中的橙色线,图中D点到目标点的距离为:(两个对角线长度)+(一个水平长度)=2x14+10=38。
左上角的数字代表F值: 即F= G+H。
箭头: 箭头的指向为该节点的父节点,可看到此时箭头均指向A,因为这些节点是由当前节点A扩展出来的,所以A为这些节点的父节点。
棕色的节点:表示这些节点在开启列表中。
蓝色的节点:表示这些节点在关闭列表中。
接下来我们又要搜索“开启列表”中F值最小的,可以看出图中F值最小的是44,但是有两个44,随便选择一个即可,暂且选择右下角的那一个44吧,好,我们看图说话:
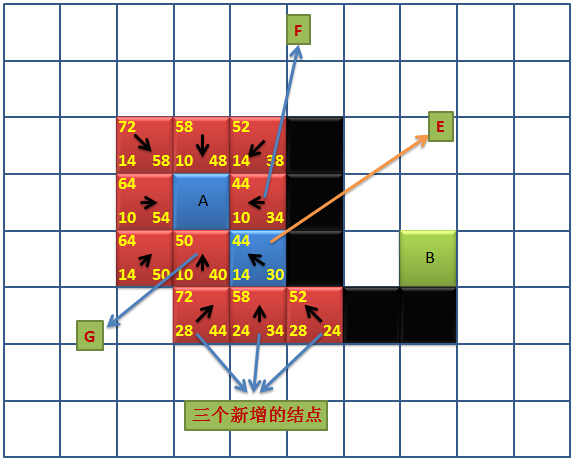
首先,将我们选中的节点添加进“关闭列表”(图中E点),将E标识为“当前节点”,然后添加其邻近的节点(如图:三个新增的节点),添加新节点时,要忽略障碍物(图中黑色部分),因为障碍物是不可以走的,首先计算三个新增节点G值,此时G值应该这样计算(以E点正下方的节点为例),E点正下方的节点为到E点的距离为10,E点到A点的距离为14,所以E点正下方的节点G值为24,并且箭头指向其父节点E。注意(重点): E点邻近的节点还有F、G两个节点(A点已在关闭列表中,忽略检查),但是F、G是之前存在“开启列表”中的,所以我们还要检查这两个点是否需要更新?我们知道,所有E点邻近的点,都有可能成为下一步要走的节点,若此时从E点走向G点,那么路径变为:A→E→G,那么G点的G值为:A到E的距离+E到G的距离= 14+10 = 24,而G点的F值变为:24+40=64。如果将G点更新,那么G点新的F值64比之前的F值50还要大,所以,G点不应该更新,因为我们是为了找更短的路径,F值变大,意味着路径变长,显然是不可取的,所以在这里,我们保持G点状态,同理,F点也是如此。至此,我们得出结论:
1、一个节点的G值不是一成不变的,与路径的变化有关,但是一个节点的H值是一定的,因为一个节点到目标点的距离总是不变的;
2、一个节点是否需要更新,看其F值在其路径发生变化后是增大还是减小,如果因为新路径导致节点F值变大,则不更新,如果F值变小,则更新为小的F值。
现在我们找到了一个“最好位置”,并且添加了新的节点,检查了节点更新情况,那么现在我们又要来搜索下一个了,判断“开启列表”中所有节点,发现还有一个F值为44的节点,毋庸置疑,它是列表中F值最小的节点,依然选择它作为“当前节点”,其周围没有空节点,所以不需要添加新节点,但是有三个邻近的节点在“开启列表”中,上图:
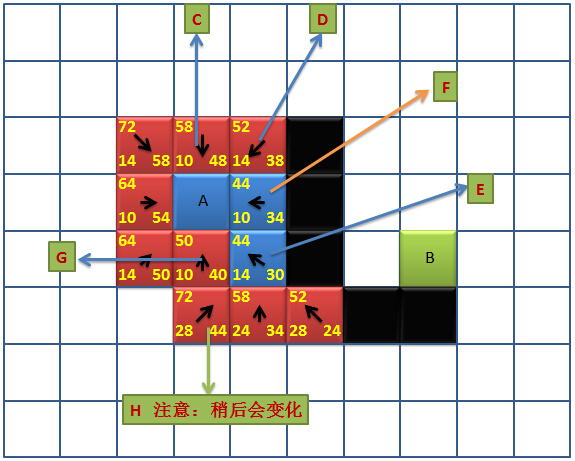
显然,无论从F→D,还是从F→G,或者是从F→C,都会使这三个节点的F值变大,所以我们不更新此三个节点,让它们保持原有状态。
熟能生巧嘛,我们最后再按上面的步骤跟着搜索一次:搜索F值最小的节点作为当前节点,此时G节点的F值为50,是最小的,我们将其从“开启列表”中移除,添加进“关闭列表”,标识为“当前节点”,照例,附上一张图:
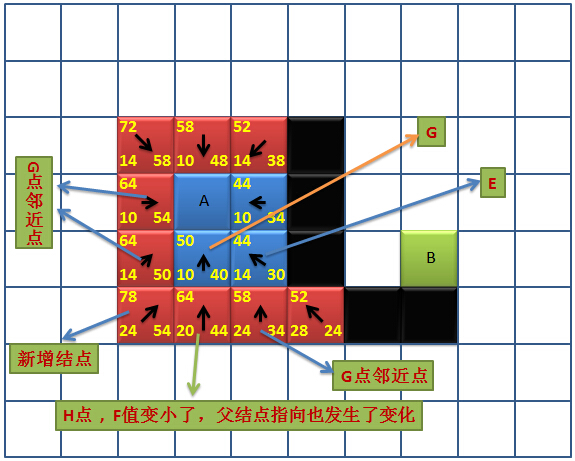
图中,G点已被置为当前节点,也新增了一个节点,其邻近的节点中有4个是之前已经在“开启列表”中的节点,我们检查是否需要更新,请仔细观察图中的H节点,上张图的H节点的F值为72,箭头指向E节点,也就是其父节点为E,到H点的路径为:A→E→H,而此时,H节点的F值更新为64,父节点也发生了变化,箭头指向G点,这是为什么呢?因为H点是G点的邻近点,此时由A→G→H的路径,显然比之前A→E→H更短,所以我们更新H点的信息,其父节点也改为G点,因为H点的状态是因为G改变的。
好啦,不多说了,相信大家经过几次的重复的步骤,应该清楚了整个寻路的流程,现在附上完整的寻路图:
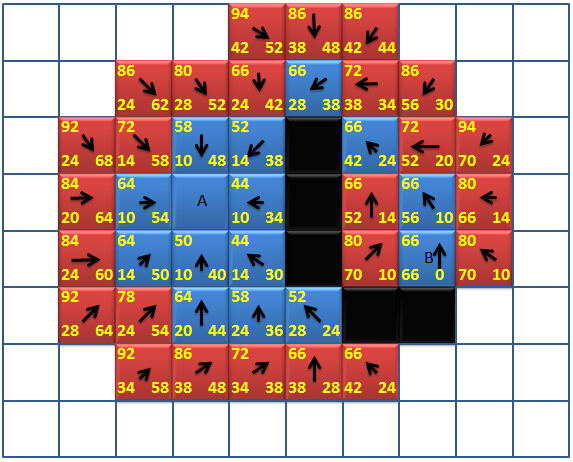
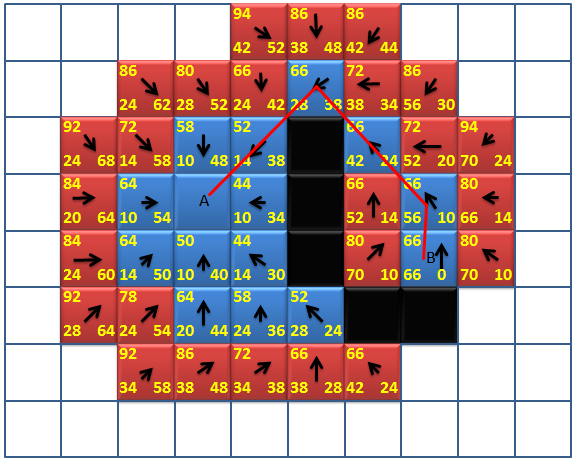
很壮观有木有?现在问题来了,这么多节点连在一起,到底哪条路径才是我们要找的路径呢?Don’t worry!大家看到箭头了没有,现在箭头的作用就发挥出来的,每个箭头只有一个方向,都标识着父节点,相当于标记着“来时的路”,现在我们要走回去了,所以我们就从目标点(B点)开始找回去的路,找B点的父节点,再找其父节点的父节点。。。一直岩着箭头(→)找到A点,那一条就是我们要找的最短的路径。如图红色线所示:
总结
A*算法具体步骤如下:
1、首先将起始点添加进“开启列表”。
2、重复如下步骤:
a) 寻找开启列表中F值最低的节点。我们称其为“当前节点”。
b) 把它从“开启列表”中移除,并添加进“关闭列表”。
c) 检查“当前节点”是否是“目标节点”
* 如果是,停止搜索,跳到第 3 步;
* 如果不是,继续下面步骤……
d) 寻找“当前节点”邻近的节点
* 如果它不可通过或者已经在关闭列表中,略过它。反之如下。
* 如果它不在开启列表中,把它添加进开启列表。把当前节点作为这一节点的父节点。记录这一格的F,G,和H值。
* 如果它已经在开启列表中,检查新路径对它G值的产生的影响
a. 如果它的G值因为新路径变大,那么保持原来的状态,不作任何改变;
b. 如果G值变小,说明新路径更好,将其父结点改为“当前结点”,更新G和F值。
e) 检查列表是否为空,如果为空,说明路径未找到,直接返回,不继续任何步骤。
3、保存路径。从目标节点开始,沿着每一节点的父节点移动直到回到起始节点。这就是我们要找的路径。 A*寻路算法采用启发式搜索方法,避免了很多无谓的搜索,提高了效率,但是如果我们想搜索的更精确,可以将方格分割得更小,但是方格越多,搜索越慢,在时间上是成指数级增长的,这也是A*算法的一大缺点,但是依然有优化的办法,使用二叉堆,关于二叉堆优化A*算法的方法,我们有机会再探讨。
注:如非特别说明,本博客的博文均为原创,如需转载请注明出处,本文链接:http://blog.csdn.net/yiyikela/article/details/46134339,尊重他人的劳动成果,谢谢!





 本文深入解析A*寻路算法,从启发式搜索、路径评分到算法描述,全面阐述如何利用方格系统找到从起点到终点的最短路径。通过实例演示估价函数的应用,解释如何通过F值最小化找到最优路径,并最终通过箭头指示路径回溯过程。
本文深入解析A*寻路算法,从启发式搜索、路径评分到算法描述,全面阐述如何利用方格系统找到从起点到终点的最短路径。通过实例演示估价函数的应用,解释如何通过F值最小化找到最优路径,并最终通过箭头指示路径回溯过程。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








